Charakterystyka ruchu prostoliniowego, typy i przykłady

On Ruch prostoliniowy Jest to taki, w którym telefon komórkowy porusza się wzdłuż linii prostej, a zatem przechodzi w wymiarze, a zatem również otrzymuje nazwę Ruch jednoznaczny. Ta linia prosta jest trajektoria lub ścieżka, a następnie obiekt, który się porusza. Samochody podróżujące wzdłuż alei na rycinie 1 podążają za tym typem ruchu.

To najprostszy model ruchu, który można sobie wyobrazić. Codzienne ruchy ludzi, zwierząt i rzeczy często łączą transfery w linii prostej z ruchami wzdłuż krzywych.

Rysunek 1. Samochody poruszające się wzdłuż prostoliniowej alei. Źródło: Pixabay.

Oto kilka dobrych przykładów:

- Podczas biegania wzdłuż 200 -metrowej prostoliniowej ścieżki.

- Prowadzenie samochodu po prostej drodze.

- Swobodne upuszczanie obiektu z pewnej wysokości.

- Kiedy piłka jest rzucana pionowo.

https: // giphy.COM/GIFS/J5XX3BYNAQV06WTOXQ

Teraz cel opisania ruchu osiąga się poprzez określenie cech, takich jak:

- Pozycja

- Przemieszczenie

- Prędkość

- Przyśpieszenie

- Czas.

Aby obserwator mógł wykryć ruch obiektu, konieczne jest posiadanie punktu odniesienia (pochodzenia o) i ustanowić określony adres, na którym można się poruszać, który może być osą X, Oś I lub jakikolwiek inny.

Jeśli chodzi o obiekt, który się porusza, może to mieć niezliczone sposoby. W tym względzie nie ma ograniczeń, jednak we wszystkim, co następuje, zostanie założone, że telefon komórkowy jest cząsteczką; obiekt tak mały, że jego wymiary nie są istotne.

Wiadomo, że nie dotyczy to obiektów makroskopowych; Jest to jednak model z dobrymi wynikami w opisie globalnego ruchu obiektu. W ten sposób cząsteczką może być samochód, planeta, osoba lub inny przedmiot, który się porusza.

Rozpoczniemy nasze badanie kinematyki prostoliniowej z ogólnym podejściem do ruchu, a następnie poszczególne przypadki zostaną zbadane jako te już mianowane.

[TOC]

Ogólne cechy ruchu prostoliniowego

Poniższy opis jest ogólny i ma zastosowanie do dowolnego rodzaju ruchu jednego wymiaru. Pierwszą rzeczą jest wybranie systemu referencyjnego. Linia, wzdłuż której ma miejsce ruch, będzie osi X. Parametry ruchu:

Pozycja

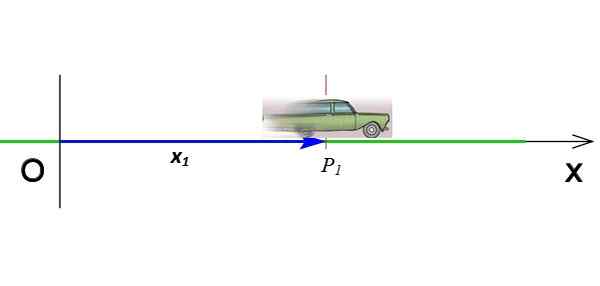Rysunek 2. Pozycja telefonu komórkowego, który porusza się po osi x. Źródło: Wikimedia Commons (zmodyfikowane przez F. Zapata).

Jest to wektor, który przechodzi od pochodzenia do punktu, w którym obiekt jest w danym momencie. Na rycinie 2 wektor X₁ Wskazuje pozycję telefonu komórkowego, gdy jest ona w współrzędnej P₁ i z czasem T₁. Jednostki wektorowe pozycji w systemie międzynarodowym są metry.

Przemieszczenie

Przemieszczenie jest wektorem wskazującym zmianę pozycji. Na rycinie 3 samochód przeszedł z pozycji P₁ do pozycji P₂, Dlatego jego przemieszczenie wynosi δX = X₂ - X₁. Przemieszczenie jest odejmowaniem dwóch wektorów, jest symbolizowane z literą grecką δ („delta”) i z kolei wektor. Jego jednostki w systemie międzynarodowym są metry.

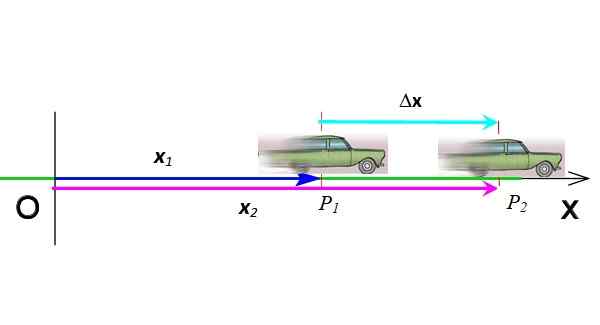Rysunek 3. Przemieszczenie wektora. Źródło: Przygotowane przez F. Zapata.

Wektory są oznaczone odważnym tekstem w wydrukowanym. Ale będąc w tym samym wymiarze, w razie potrzeby możesz obejść się bez notacji wektorowej.

Może ci służyć: gałęzie klasycznej i nowoczesnej fizyki

Przebyty dystans

Dystans D Zwiedzony ruchomym obiektem jest wartość bezwzględna wektora przemieszczenia:

D = ΙXΙ = δX

Będąc wartością bezwzględną, przejechana odległość jest zawsze większa lub równa 0, a jej jednostki są takie same jak w pozycji i przesunięciu. Notację wartości bezwzględnej można wykonać za pomocą pasków modułów lub po prostu usuwanie odważnej litery w drukowanym tekście.

Średnia prędkość

Jak szybko zmienia się pozycja? Istnieją powolne i szybkie telefony komórkowe. Kluczem zawsze była prędkość. Aby przeanalizować ten czynnik, analizowana jest pozycja X funkcja czasu T.

Średnia prędkość v_M (Patrz rysunek 4) Jest to nachylenie linii suszenia (fuksia) do krzywej X vs T i dostarcza globalnych informacji o przemieszczeniu mobilnym w rozważanym przedziale czasu.

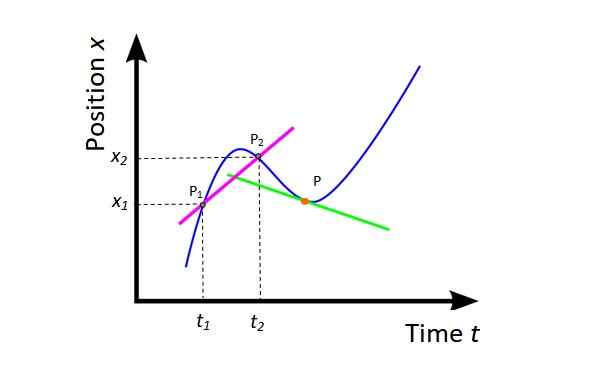Rysunek 4. Średnia prędkość i natychmiastowa prędkość. Źródło: Wikimedia Commons, zmodyfikowane przez F. Zapata.

v_M = (X₂ - X₁) / (T₂ -T₁) = ΔX / ΔT

Średnia prędkość to wektor, którego jednostki w systemie międzynarodowym są metry /sekunda (SM).

Chwilowa prędkość

Średnia prędkość jest obliczana przez wykonanie mierzalnego przedziału czasu, ale nie informuje o tym, co dzieje się we wspomnianym przedziale. Aby poznać prędkość w dowolnym momencie, musisz sprawić, by przedział czasu był bardzo mały, matematycznie jest to równoważne:

ΔT → 0

Równanie jest wcześniej podawane dla średniej prędkości. W ten sposób uzyskana jest szybkość chwilowej lub po prostu prędkości:

Geometrycznie, pochodną pozycji w odniesieniu do czasu jest nachylenie stycznej linii do krzywej X vs T w danym momencie. Na rycinie 4 punkt jest pomarańczowy, a linia styczna jest zielona. Natychmiastowa prędkość w tym momencie jest nachyleniem tej linii.

Prędkość

Prędkość jest definiowana jako moduł wartości bezwzględnej lub prędkości i jest zawsze dodatnia (sygnalizacja, drogi i autostrady są zawsze pozytywne, nigdy ujemne). Terminy „prędkość” i „prędkość” mogą być używane codziennie, ale w fizyce konieczne jest rozróżnienie między wektorem a wspinaczką.

v = ΙvΙ = v

Średnie przyspieszenie i natychmiastowe przyspieszenie

Prędkość może się zmienić w trakcie ruchu, a rzeczywistość jest taka, że ​​oczekuje się, że to zrobi. Istnieje wielkość, która kwantyfikuje tę zmianę: przyspieszenie. Jeśli zauważymy, że prędkość jest zmianą pozycji w odniesieniu do czasu, przyspieszenie to zmiana prędkości w odniesieniu do czasu.

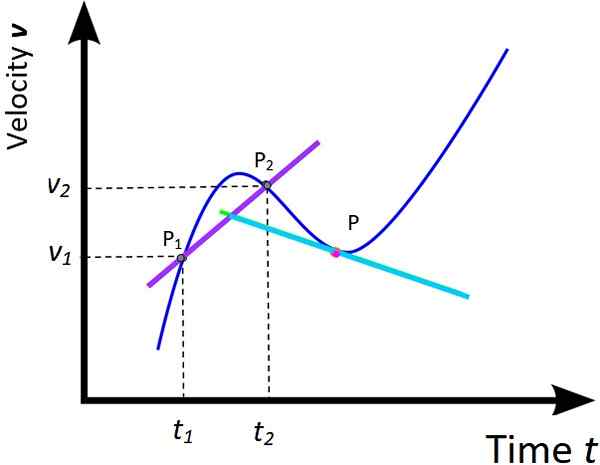Rysunek 5. Średnie przyspieszenie i natychmiastowe przyspieszenie. Źródło: Wikimedia Commons, zmodyfikowane przez F. Zapata.

Leczenie podane na wykres X vs T z dwóch poprzednich sekcji można rozszerzyć na odpowiedni wykres v vs T. W związku z tym średnie przyspieszenie i natychmiastowe przyspieszenie są zdefiniowane jako:

Do_M = (v₂ - v₁) / (T₂ -T₁) = Δv / ΔT  (W oczekiwaniu na siedzibę)

Przyspieszenie i Opóźnienie

W jednym ruchu wektory według konwencji mają pozytywne lub negatywne znaki, gdy idą w taki czy inny sposób. Kiedy przyspieszenie ma takie samo znaczenie co prędkość, zwiększa swoją wielkość, ale gdy ma to przeciwny sens, a prędkość zmniejsza jego wielkość. Następnie mówi się, że ruch jest opóźniony.

Może ci służyć: Leyden Butelka: części, operacja, eksperymenty

Chłopaki

Klasyfikacja ruchów prostoliniowych jest zwykle wykonywana na podstawie:

- Czy przyspieszenie jest stałe.

- Ruch przechodzi wzdłuż linii poziomej lub pionowej.

Ruch z ciągłym przyspieszeniem

https: // giphy.com/gifs/ylzfnbidhm7rp391fi

Gdy przyspieszenie jest stałe, średnie przyspieszenie Do_M Jest to równe natychmiastowym przyspieszeniu Do I są dwie opcje:

- Że przyspieszenie jest warte 0, w którym to przypadku prędkość jest stała i ma jednolity ruch prostoliniowy lub MRU.

- Stałe przyspieszenie różni się od 0, w których prędkość rośnie lub maleje liniowo z czasem (ruch prostoliniowy równomiernie zmienny lub MRUV):

Gdzie v_F  I T_F Są to odpowiednio ostatnia prędkość i czas i v_albo I T_albo Są to początkowe prędkość i czas. Tak T_albo = 0, Podczas wyczyszczenia ostatniej prędkości masz już równanie dla ostatecznej prędkości:

v_F = v_albo + NA

W przypadku tego ruchu ważne są również ważne równania:

- Pozycja w zależności od czasu: x = x_albo + v_{albo .}t +½ w²

- Prędkość w zależności od pozycji: v_F² = v_albo² + 2.ΔX  (Z δx = x - x_albo)

Ruchy poziome i ruchy pionowe

Ruchy poziome to te, które przechodzą wzdłuż osi poziomej lub osi x, podczas gdy pionowe robią to wzdłuż osi i osi. Ruchy pionowe pod działaniem grawitacji są najczęstsze i interesujące.

W poprzednich równaniach jest przyjmowany A = g = 9.8 m/s² skierowany pionowo, kierunek, który prawie zawsze jest wybierany z znakiem ujemnym.

Tą drogą, v_F = v_albo + NA To się zmienia v_F = v_albo - Gt A jeśli początkowa prędkość wynosi 0, ponieważ obiekt został upuszczony swobodnie, jest on bardziej uproszczony v_F = - gt. Oczywiście, o ile nie bierze się pod uwagę opór powietrza.

Rozwiązane przykłady

Przykład 1

W punkcie uwolniono mały pakiet, aby poruszał się wzdłuż transportera z przesuwnymi kółkami ABCD pokazanymi na rysunku. Pakiet przechodzący przez nachylone sekcje AB i CD, pakiet ma przyspieszenie 4,8 m/s², podczas gdy w sekcji poziomej BC utrzymuje stałą prędkość.

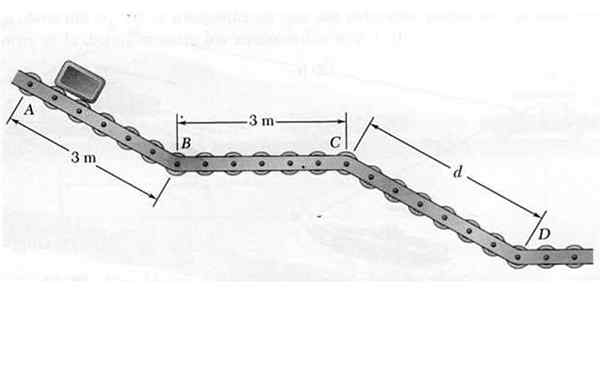Rysunek 6. Pakiet, który porusza się po przesuwnej ścieżce rozwiązanego przykładu 1. Źródło: Self Made.

Wiedząc, że prędkość, z jaką osiąga się pakiet w D, wynosi 7,2 m/s, określ:

a) odległość między C i D.

b) Czas wymagany do osiągnięcia końca.

Rozwiązanie

Ruch pakietu jest przeprowadzany w trzech pokazanych sekcjach prostoliniowych i aby obliczyć żądane, prędkość jest wymagana w punktach B, C i D. Przeanalizujmy każdą sekcję osobno:

Sekcja ab

Ponieważ czas nie jest dostępny w tej sekcji, będzie on używany v_F² = v_albo² + 2.ΔX  Z VO = 0:

v_F² = 2a.Δx → v_F²= 2. 4,8 m/s² . 3 m = 28.8 m²/S² → v_F  = 5.37 m/s = v_B

Czas, jaki pakiet zabrał do podróży w sekcji AB, to:

T_Ab = (v_F - v_albo) /A = 5.37 m/s/4,8 m/s² = 1.19 s

Sekcja BC

Dlatego prędkość w sekcji BC jest stała v_B = v_C = 5.37 m/s. Czas potrzebny na podróżowanie w tej sekcji to:

Może ci służyć: światła załamanie: elementy, prawa i eksperyment

T_pne = odległość _pne  / v_B = 3 m/ 5.37 m/s = 0.56 s

Sekcja CD

Początkowa prędkość tego sekcji to v_C = 5.37 m/s, Ostateczna prędkość jest v_D = 7,2 m/s, przez v_D²  = v_C² + 2. Do. D Wartość D:

D = (v_D²  - v_C²)/2.a = (7.2²  - 5.37²)/2 X 4.8 m = 2.4 m

Czas jest obliczany jako:

T_{CD =} (v_D  - v_C)/A = (7.2-5.37)/ 4.8 s = 0.38 s.

Odpowiedzi na zadane pytania to:

a) d = 2.4 m

b) Czas podróży to T_Ab + T_pne + T_{płyta CD} = 1.19 s +0.56 S +0.38 s = 2.13 s.

Przykład 2

Osoba znajduje się pod poziomą bramą, która jest początkowo otwarta i wysokość 12 m. Osoba pionowo uruchamia obiekt w kierunku bramy z prędkością 15 m/s.

Wiadomo, że brama zamyka 1,5 sekundy po uruchomieniu obiektu z wysokości 2 metrów. Odporność na powietrze nie będzie brana pod uwagę. Odpowiedz na następujące pytania, uzasadniając:

a) Czy udaje ci się przekazać obiekt przez bramę, zanim się zamknie?

b) Czy obiekt kiedykolwiek zderzy się z zamkniętą bramą? Jeśli potwierdza, kiedy to się stanie?

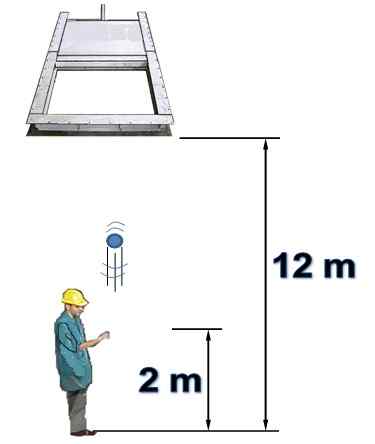Rysunek 7. Obiekt jest uruchamiany pionowo (rozwiązany przykład 2). Źródło: Self Made.

Odpowiedz)

Istnieje 10 metrów między początkową pozycją piłki a bramą. Jest to pionowe uruchomienie, w którym ten adres jest uznawany za pozytywny.

Możesz dowiedzieć się, jaka prędkość, którą niesie, po przybyciu w tym momencie, z tym wynikiem czasu, aby to zrobić i porównać z czasem zamknięcia bramy, czyli 1.5 sekund:

v_F ²= v_albo ²- 2.G. Δi → v_F = (15² - 2 X 9.8 X10)^1/2 M = 5.39 m/s

T = (v_F - v_albo) /g = (5.39 - 15) / (-9.8) S = 0.98 s

Ponieważ ten czas jest mniejszy niż 1.5 sekund, a następnie stwierdza się, że obiekt może przejść przez bramę przynajmniej raz.

Odpowiedź b)

Wiemy już, że obiekt zarządza. Prędkość, gdy sięgnie na wysokości bramki, ma taką samą wielkość, jak w górę, ale w przeciwnym kierunku. Dlatego pracuj z -5.39 m/s, a czas potrzebny do osiągnięcia tej sytuacji jest:

T = (v_F - v_albo) /G = (-5.39 - 15) / (-9.8) S = 2.08 s

Ponieważ brama pozostaje otwarta tylko dla 1.5 s, oczywiste jest, że nie ma czasu, zanim się zamknie, ponieważ okaże się, że jest zamknięty. Odpowiedź brzmi: obiekt, jeśli zderzy się z zamkniętą bramą po 2.08 sekund po uwolnieniu, kiedy nastąpi po zejściu.

Bibliografia

1. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).69-116.
2. Giancoli, zm. Fizyka. (2006). Zasady z aplikacjami. 6^th Wydanie. Prentice Hall. 22-25.
3. Kirkpatrick, L. 2007. Fizyka: spojrzenie na świat. 6^ta Skrócone wydanie. Cengage Learning. 23 - 27.
4. Resnick, r. (1999). Fizyczny. Tom 1. Trzecie wydanie po hiszpańsku. Meksyk. Continental Editorial Company S.DO. c.V. 21-22.
5. Rex, a. (2011). Podstawy fizyki. osoba. 33 - 36
6. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14^th. Wyd. Tom 1. 50 - 53.
7. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7^mama. Wydanie. Meksyk. Redaktorzy edukacyjni Cengage. 23-25.
8. Serway, r., Vulle, c. (2011). Podstawy fizyki. 9^na Wyd. Cengage Learning. 43 - 55.
9. Wilson, J. (2011). Fizyka 10. Edukacja Pearsona. 133 - 149.