Charakterystyka linii prostopadłej, przykłady, ćwiczenia

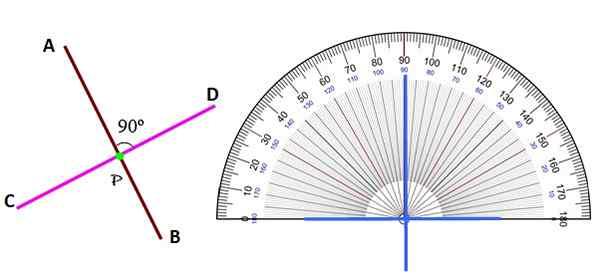
A Linia prostopadła To taki, który tworzy kąt 90º w stosunku do innej linii, krzywej lub powierzchni. Zauważ, że gdy dwie linie są prostopadłe i na tej samej płaszczyźnie, po cięcie tworzą cztery identyczne kąty, każde z 90º.

Jeśli jeden z kątów nie jest 90º, mówi się, że linie są ukośne. Linie prostopadłe są częste pod względem projektowania, architektury i konstrukcji, na przykład sieć rur następującego obrazu.

Rysunek 1. Prosta rura i liczne linie prostopadłe. Ile kątów 90º można policzyć na tym obrazie? Źródło: Piqsels.

Orientacja linii prostopadłych może być zróżnicowana, na przykład pokazana poniżej:

Rysunek 2. Linie prostopadłe na płaszczyźnie. Źródło: f. Zapata.

Niezależnie od pozycji, linie prostopadłe są rozpoznawane przez identyfikację kąta między nimi jako 90º, za pomocą przenośnika.

Zauważ, że w przeciwieństwie do równoległych linii w płaszczyźnie, które nigdy nie są przecinające się, prostopadle zawsze robią to w punkcie P, nazywane stopa jednej z linii na drugiej. Dlatego też są dwie linie prostopadłe Sekundy.

Każda linia ma nieskończoną prostopadłą do niej, ponieważ po prostu wypierając segment AB w lewo lub w prawo w segmencie CD, będziemy mieli nowe prostopadle z inną stopą.

Jednak nazywana jest prostopadła, która przechodzi tuż przez punkt środkowy segmentu dwusieczna wspomnianego segmentu.

[TOC]

Przykłady linii prostopadłych

Linie prostopadłe są częste w krajobrazie miejskim. Na poniższym obrazie (ryc. 3) Tylko kilka z wielu prostopadłych linii docenianych na prostej fasadzie tego budynku i jego elementach, takich jak drzwi, kanały, kroki i więcej: Więcej:

Może Ci służyć: Dyskretne przekształcenie: właściwości, aplikacje, przykłady Rysunek 3. Istnieje wiele prostopadłych linii na fasadzie wspólnego budynku, takiego jak ten. Źródło: Richard Kang przez Flickr.

Dobrą rzeczą jest to, że trzy linie prostopadłe do siebie pomagają nam ustalić lokalizację punktów i obiektów w przestrzeni. Czy osie współrzędnych identyfikowane jako Oś x, Oś y I Oś z, Wyraźnie widoczne w rogu prostokątnego pokoju, takie jak następujące:

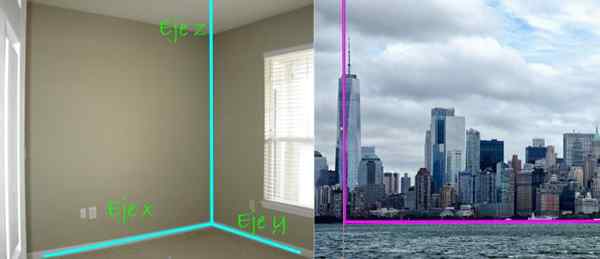Rysunek 4. System osi kartezjańskiej składa się z trzech linii prostopadłych do siebie, każda ma preferencyjny kierunek w przestrzeni. Lewy obraz obrazu: Treybunn 2 do Flickr. Właściwy obraz; Needpix.

W panoramicznym widoku miasta, po prawej stronie, ostrzega również prostopadłość między drapaczkami i ziemią. Pierwszy powiedziałby, że można go znaleźć w całym Oś z, Podczas gdy ziemia jest płaszczyzną, która w tym przypadku jest samolotem Xy.

Jeśli ziemia stanowi płaszczyznę Xy, Wieżowiec jest również prostopadle do dowolnej alei lub ulicy, co gwarantuje jego stabilność, ponieważ skłonna struktura jest niestabilna.

A na ulicach, gdziekolwiek prostokątne zakątki, istnieją prostopadłe linie. Wiele możliwości i ulic ma prostopadły układ, pod warunkiem, że na to pozwalają ziemia i wypadki geograficzne.

Aby nagle wyrazić prostopadłość między liniami, segmentami lub wektorami, używany jest symbol ⊥. Na przykład, jeśli linia l₁ jest prostopadle do linii L₂, napisaliśmy:

L₁ ⊥ l₂

Więcej przykładów linii prostopadłych

- W projekcie linie prostopadłe są bardzo obecne, ponieważ wiele wspólnych obiektów opiera się na kwadratach i prostokątach. Te czworobok charakteryzują się posiadaniem wewnętrznych kątów 90º, ponieważ ich boki mają dwa do dwóch równoległych:

Może ci służyć: ogólne równanie paraboli (przykłady i ćwiczenia)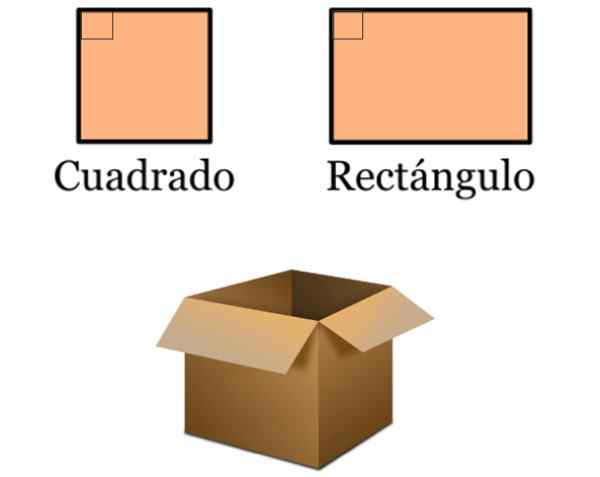 Rysunek 5. Squares i prostokąty są częścią wielu projektów, takich jak to proste kartonowe pudełko do przechowywania towarów. Źródło: f. Zapata.

- Sądy, na których praktykowane są różne sporty, są wyznaczone przez liczne kwadraty i prostokąty. Te z kolei zawierają prostopadłe linie.

- Dwa segmenty, które składają się na trójkąt prostokąta, są do siebie prostopadłe. Są one nazywane kategorie, Podczas gdy pozostała linia jest wywoływana przeciwprostokątna.

- Linie wektorowe pola elektrycznego są prostopadłe do powierzchni równowagi elektrostatycznej.

- W przypadku załadowanego kierowcy sprzęt i sprzęt są zawsze prostopadłe do elementów pola elektrycznego.

- W systemach lub kanałach rurowych używanych do transportu różnych rodzajów płynów, takich jak gaz, które pojawiają się na rycinie 1, jest powszechne dla łokci pod kątem prostym. Dlatego tworzą prostopadłe linie, tak jest w przypadku pokoju kotłowego:

Rysunek 6. Rurki w kotle. Źródło: Wikimedia Commons. Roger Mclassus/CC BY-S (http: // creativeCommons.Org/licencje/by-sa/3.0/)

Ćwiczenia

- Ćwiczenie 1

Narysuj dwie prostopadłe linie przez zasadę i kompas.

Rozwiązanie

Jest to bardzo proste, wykonując następujące kroki:

-Pierwsza linia jest narysowana, zwana AB (czarny).

-Powyżej (lub poniżej, jeśli są preferowane) punktu A ab, gdzie minie prostopadle. Jeśli P jest tuż powyżej (lub poniżej) połowy AB, powiedział, że prostopadle jest dwusektorem segmentu AB.

-Z kompasem wyśrodkowanym na p narysuje się okrąg, który przecina AB w dwóch punktach, powołany do „i B” (czerwony).

Może ci służyć: przyjazne lub przyjazne liczby: przykłady i jak je znaleźć

-Kompas w A'P jest otwarty, koncentruje się na „a okręg, które przechodzi przez p (zielony).

-Powtórz poprzedni krok, ale teraz otwiera kompas długości segmentu B'P (zielony). Oba łuki obwodu są wycięte w punkcie Q poniżej p i oczywiście w tym drugim.

-Punkty P i Q są połączone z regułą, a linia prostopadła (niebieska) jest już gotowa.

-Wreszcie wszystkie konstrukcje pomocnicze muszą być starannie wymazane, pozostawiając tylko prostopadłe.

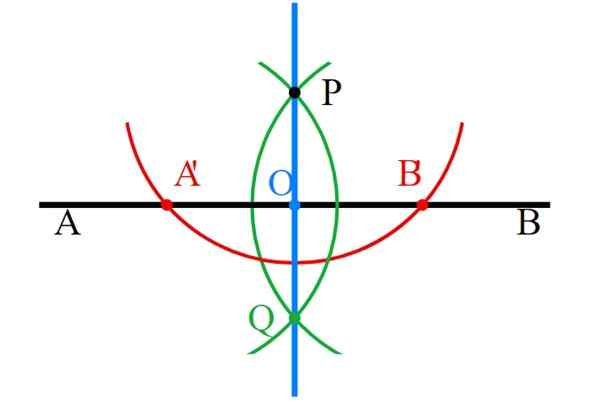Rysunek 6. Linie perfendularne z regułami i kompasami. Źródło: Wikimedia Commons.

- Ćwiczenie 2

Dwie linie l₁ i ja₂ Są prostopadłe, jeśli ich nachylenie m₁ oraz m₂ Spełniają ten związek:

M₁ = -1/m₂

Biorąc pod uwagę linię y = 5x - 2, znajdź linię prostopadłą do niej i przejdź przez punkt (-1, 3).

Rozwiązanie

-Przede wszystkim jest nachylenie prostopadłej linii m_⊥, Jak wskazano w oświadczeniu. Nachylenie oryginalnej linii to m = 5, współczynnik towarzyszący „x”. Więc:

M_⊥= -1/5

-Następnie zbudowane jest równanie linii prostopadłej i_⊥, zastąpienie wcześniej znalezionej wartości:

I_⊥= -1/5x + b

-Wówczas wartość B jest określana za pomocą punktu podanego przez oświadczenie, (-1,3), ponieważ linia prostopadła musi przez nią przejść:

y = 3

x = -1

Zastąpienie:

3 = -1/5 (-1) + B

Wartość B jest oczyszczona:

B = 3- (1/5) = 14/5

-Wreszcie zbudowano ostateczne równanie:

I_⊥= -1/5x + 14/5

Bibliografia

1. Baldor, a. 2004. Płaska i przestrzeń geometria. Publikacje kulturalne.
2. Clemens, s. 2001. Geometria z aplikacjami i rozwiązywaniem problemów. Addison Wesley.
3. Matematyka jest zabawna. Prostopadłe linie. Odzyskany z: Mathisfun.com.
4. Monterey Institute. Prostopadłe linie. Odzyskane z: Montereyinstitute.org.
5. Wikipedia. Prostopadłe linie. Odzyskane z: jest.Wikipedia.org.