Fermat ogranicza to, co polega i ćwiczenia rozwiązane

On Limit fermat Jest to metoda numeryczna stosowana do osiągnięcia wartości nachylenia linii, która jest styczna do określonej funkcji jej domeny. Jest również używany do uzyskania krytycznych punktów funkcji. Jego wyraz jest zdefiniowany jako:

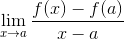
Oczywiste jest, że Fermat nie znał fundamentów pochodnej, jednak jego badania promowały grupę matematyków do zapytania o linie styczne i ich zastosowania w obliczeniach.

[TOC]

Jaki jest limit Fermata?

Składa się z podejścia 2 punktów, które w poprzednich warunkach tworzą linię sekundową do funkcji z przecięciem parami wartości.

Podchodząc do zmiennej do wartości „A”, para punktów jest zobowiązana do spotkania. W ten sposób wcześniejsza linia suszenia staje się styczna do punktu (a; f (a)).

Wartość ilorazu (x - a), oceniana w punkcie „a”, rzuca nieokreśloność limitów typu k między zero (k/0). Gdzie te nieokreśloności można przełamać różnymi technikami faktoryzacji.

Najczęściej stosowane techniki operacyjne to:

-Różnica kwadratowa (a² - B² ) = (a + b) (a - b); Istnienie elementu (A-B) implikuje w większości przypadków współczynnik upraszczający wyrażenie (x-a) w stosunku granicznym fermat.

- Kwadratowe zakończenie (Axe² + bx); Po zakończeniu kwadratów uzyskano dwumian Newton, w którym jeden z jego 2 czynników jest uproszczony za pomocą wyrażenia (x - a), łamanie nieokreśloności.

- Koniugate (a + b) / (a ​​+ b); Pomnóż i podziel wyrażenie przez koniugat pewnego czynnika może być bardzo pomocny w złamaniu nieokreśloności.

- Wspólny czynnik; W wielu przypadkach wynik obsługi licznika fermat f (x) - f (a) ukryty do współczynnika (x - a) niezbędny do faktoryzacji. W tym celu uważnie obserwuje się, jakie elementy powtarzane są w każdym czynniku wyrażenia.

Fermat Limit Zastosowanie maksymalnie i minimum

Nawet gdy limit Fermata nie rozróżnia maksimum od minimum.

Podstawowa wiedza na temat teorii graficznej funkcji w połączeniu z tym twierdzeniem może być wystarczająca do ustalenia maksymalnych i minimalnych wartości między funkcjami. W rzeczywistości punkty przegięcia mogą być zdefiniowane przez twierdzenie dodatkowej średniej wartości Twierdzenia Fermata.

Przypowieść sześcienna

Najważniejszy paradoks dla Fermat przyszedł podczas studiowania przypowieści sześciennej. Ponieważ jego uwaga była skierowana na styczne linie funkcji dla danego punktu, napotkał problem definiowania wspomnianej linii stycznej w istniejącym punkcie fleksji w funkcji.

Wydawało się niemożliwe do ustalenia linii stycznej. W ten sposób rozpoczyna się dochodzenie, które spowodowałoby powstanie rachunku różnicowego. Następnie zdefiniowane przez ważnych wykładników matematyki.

Maximus i minimalny

Badanie maksimum i minimum funkcji było wyzwaniem dla klasycznej matematyki, w której jednoznaczna i praktyczna metoda definicji ich.

Fermat stworzył metodę opartą na obsłudze małych wartości różnicowych, które po procesach faktoryzacji są eliminowane poprzez ustalenie miejsca najwięcej i minimalnej wartości.

Zmienną tę należy ocenić w pierwotnym wyrażeniu, aby określić współrzędną wspomnianego punktu, który wraz z kryteriami analitycznymi zostanie zdefiniowany przez maksymalny lub minimalny wyrażenia.

metoda

W swojej metodzie Fermat używa dosłownej symboliki Viety, która polegała na wyłącznym użyciu liter kapitałowych: samogłosek, dla niewiadomych i spółgłosek dla znanych ilości.

W przypadku wartości radykalnych Fermat wdrożył konkretny proces, który później zostałby wykorzystany w czynnikach limitów nieokreśloności nieskończoność między nieskończonością.

Proces ten polega na podzieleniu każdego wyrażenia przez zastosowaną wartość różnicową. W przypadku Fermat użyła litery E, gdzie po podziale między największą mocą E, wartość poszukiwana z punktu krytycznego staje się jasna.

Historia

Limit Fermata jest w rzeczywistości jednym z najmniej znanych wkładów na długą listę matematyka. Jego badania pochodziły z liczb pierwszych, aby w zasadzie stworzyć podstawy do obliczeń.

Z kolei Fermat był znany ze swoich ekscentryczności dotyczących swoich hipotez. To było powszechne dla rodzaju wyzwania dla innych matematyków tamtych czasów, kiedy miał już rozwiązanie lub demonstrację.

Miał wiele różnych sporów i sojuszy z różnymi matematykami tamtych czasów, którzy kochali lub nienawidzą pracy z nim.

Jego ostatnie twierdzenie było głównym odpowiedzialnym za jego światową sławę, w której powiedział, że uogólnienie twierdzenie Pitagorasa W przypadku każdego stopnia „N” było to niemożliwe. Mówi się, że ma ważną demonstrację, ale zmarł przed upublicznieniem.

Ta demonstracja musiała czekać około 350 lat. W 1995 r. Matematycy Andrew Wiles i Richard Taylor zakończyli lęk pozostawiony przez Fermata, pokazując, że miał rację poprzez ważną demonstrację swojego ostatniego twierdzenia.

Ćwiczenia

Ćwiczenie 1

Zdefiniuj nachylenie stycznej linii do krzywej f (x) = x² W punkcie (4, 16)

Zastąpienie wyrażenia limitu Fermat:

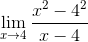
Następnie stosowanie minimum kwadratowych licznik jest współczynnikiem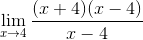

Czynniki są uproszczone (x - 4)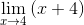

Podczas oceny

M = 4 + 4 = 8

Ćwiczenie 2

Zdefiniuj krytyczny punkt ekspresji f (x) = x² + 4x za pomocą limitu fermat

W takim przypadku nie ma współrzędnej, więc wartość x jest zastępowana przez ogólny formularz x₀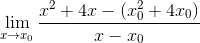

Przeprowadzane jest strategiczne grupowanie elementów, starając się grupować rówieśników X-X₀

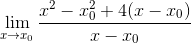
Kwadraty są opracowywane

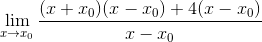
Obserwuje się wspólny czynnik X-X_{0 i jest wyodrębniony}

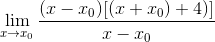
Wyrażenie może być już uproszczone, a nieokreślone jest złamanie

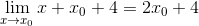
W minimalnych punktach wiadomo, że nachylenie linii stycznej jest równe zero. W ten sposób możemy dopasować zero wyrażenia i wyczyścić wartość x₀    

2 x₀ + 4 = 0

X₀ = -4/2 = -2

Aby uzyskać brakujące współrzędne, musisz tylko ocenić punkt w pierwotnej funkcji

F (-2) = (-2)² + 4 (-2) = 4 - 8 = - 4

Krytyczny jest punkt P (-2, -4).

Bibliografia

1. Prawdziwa analiza. Historyczne podejście Sauhl Stahl, John Wiley & Sons, 5 sierpnia. 1999.
2. Kariera matematyczna Pierre autorstwa Fermata, 1601-1665: Drugie wydanie. Michael Sean Mahoney. Princeton University Press, 5 czerwca. 2018
3. Od Fermat do Minkowskiego: Wykłady na temat teorii liczb i jej historycznego rozwoju. W. Scharlau, godz. Opolka, Springer Science & Business Media, 1985
4. Ostatnie twierdzenie Fermata: genetyczne wprowadzenie do teorii liczb algebraicznych. Harold m. Edwards. Springer Science & Business Media, 14 stycznia. 2000
5. Fermat dni 85: Matematyka do optymalizacji. J.-B. Hiriart-sury Elsevier, 1 stycznia. 1986