Blokowe elementy algebry, przykłady, ćwiczenia rozwiązane

On Blokuj algebrę Odnosi się do zestawu operacji wykonywanych przez bloki. Te i niektóre więcej elementów służą schematycznie reprezentując system i łatwo wizualizować twoją odpowiedź na określony wpis.

Zasadniczo system zawiera różne elementy elektryczne, elektroniczne i elektromechaniczne, a każdy z nich, z ich odpowiednią funkcją i pozycją w systemie, a także sposób, w jaki są powiązane, jest schematyzowane przez bloki funkcjonalne.

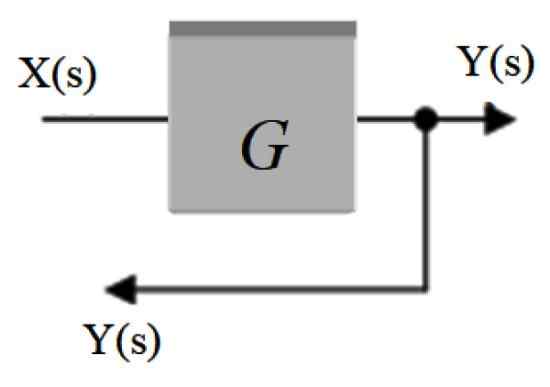
Rysunek 1.

Na powyższym rysunku znajduje się bardzo prosty system, który składa się z sygnału wejściowego x (s), który wchodzi do bloku z funkcją transferu G (S), który go modyfikuje i wytwarza wyjściowe Y (S).

Wygodne jest reprezentowanie sygnałów i ich podróży przez system przez strzały, które wchodzą i opuszczają każdy blok. Zwykle przepływ sygnału jest skierowany od lewej do prawej.

Zaletą tego rodzaju schematu jest pomoc wizualna, jaką zapewnia zrozumienie systemu, chociaż nie stanowi on fizycznej reprezentacji tego samego. W rzeczywistości schemat blokowy nie jest wyjątkowy, ponieważ według punktu widzenia można narysować nawet kilka schematów tego samego systemu.

Może się również zdarzyć, że ten sam schemat jest używany dla kilku systemów, które niekoniecznie są ze sobą powiązane, pod warunkiem, że jego zachowanie odpowiednio opisuje. Istnieją różne systemy, których odpowiedź jest podobna w wielu aspektach, na przykład obwód LC (kanał indukcyjny) i system resortowy.

[TOC]

Co to jest schemat blokowy?

Systemy są zwykle bardziej skomplikowane niż na rycinie 1, ale algebra blokowa zapewnia serię prostych reguł manipulowania schematem systemu i zmniejszenia go do najprostszej wersji.

Jak wyjaśniono na początku, schemat wykorzystuje bloki, strzałki i kół do ustalenia związku między każdym komponentem systemowym a przepływem sygnałów, które przez niego przebiegają.

Algebra blokowa pozwala porównać dwa lub więcej sygnałów poprzez ich sumę, odejmowanie i mnożenie, a także analizować wkład, jaki każdy komponent wnosi w system.

Dzięki temu można zmniejszyć cały system do jednego sygnału wejściowego, unikalnej funkcji transferu, która całkowicie opisuje działanie systemowe i odpowiadające wyjście.

Może ci służyć: astroclymy: historia, jakie studia, gałęzie

Elementy schematu blokowego

Elementy schematu blokowego są następujące:

Sygnał

Sygnały są bardzo zróżnicowane, na przykład często jest to prąd elektryczny lub napięcie, ale może być jasne, dźwięk i więcej. Ważne jest to, że zawiera informacje o określonym systemie.

Sygnał jest oznaczony kapitałem, jeśli jest funkcją zmiennej S transformacji Laplace: x (patrz rysunek 1) lub z małymi literami, jeśli jest on oparty na czasie T, jako x (t).

Na schemacie blokowym sygnał wejściowy jest reprezentowany przez strzałkę skierowaną w kierunku bloku, podczas gdy sygnał wyjściowy, oznaczony jako Y (s) lub (t), jest wskazany z wychodzącą strzałką.

Zarówno sygnał wejściowy, jak i wyjściowy są unikalne, a adres, w którym przepływy informacji są określone przez kierunek strzałki. A algebra jest taka sama dla jednej z dwóch zmiennych.

Blok

Blok jest reprezentowany przez kwadrat lub prostokąt (patrz rysunek 1) i może być używany do przeprowadzania operacji lub wdrożenia funkcji transferu, który zwykle jest oznaczony kapitałem G. Ta funkcja jest modelem matematycznym, w którym odpowiedź oferowana przez system jest opisana przed sygnałem wejściowym.

Funkcję transferu można wyrazić w kategoriach czasu T takie jak g (t) lub zmienna S Jak G (s).

Gdy sygnał wejściowy X (S) dociera do bloku, jest on mnożony przez funkcję przesyłania i przekształca się w sygnał wyjściowy Y (S). Matematycznie wyraża się to w następujący sposób:

I (s) = x (s).G (s)

Równie funkcja przenoszenia jest stosunek między transformacją Laplace sygnału wyjściowego a transformacją Laplace sygnału wejściowego, pod warunkiem, że początkowe warunki układu są zerowe:

G (s) = y (s) / x (s)

Suma

Suma lub lato jest symbolizowane przez okrąg z krzyżem w środku. Służy do łączenia, według sum i odejmowania, dwa lub więcej sygnałów. Na końcu strzałki, która symbolizuje sygnał, znak + jest umieszczony bezpośrednio, jeśli ten sygnał jest dodany lub znak - jeśli jest odejmowany.

Na poniższym rysunku jest przykład, jak działa lato: masz sygnał wejściowy x, do którego dodawane są sygnały a i b, uzyskując w rezultacie wyjście i, które algebraicznie równa się:

Może ci służyć: ujęcie pionowe: wzory, równania, przykłady

Y = x+a+b

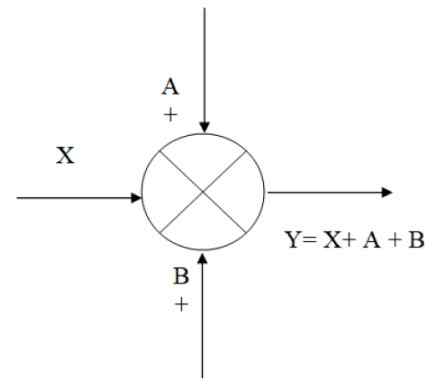Rysunek 2. Przykład egzekwowania. Źródło: f. Zapata.

Punkt rozgałęzienia

To się nazywa Punkt rozwidlenia. W nim sygnał wychodzący z bloku jest rozmieszczony na inne bloki lub pióropusz. Jest reprezentowany przez punkt umieszczony na strzałce sygnału, a kolejna strzałka pochodzi z niego, który przekierowuje sygnał w kierunku innej części.

Rysunek 3. Punkt rozgałęzienia. Źródło: f. Zapata.

Przykłady bloków algebry blokowej

Jak wyjaśniono wcześniej, pomysł polega na wyrażeniu systemu przez schemat bloków i zmniejszenie go, aby znaleźć funkcję przeniesienia, która go opisuje. Poniżej przedstawiono reguły algebry blokowej w celu uproszczenia diagramów:

Bloki kaskadowe

Kiedy masz sygnał, który przechodzi sukcesowo przez bloki G₁, G₂, G₃..., jest zredukowane do unikalnego bloku, którego funkcja transferu jest iloczynem g₁, G₂, G₃..

W poniższym przykładzie sygnał X (S) wchodzi do pierwszego bloku, a jego wyjście to:

I₁(s) = x (s).G₁(S)

Rysunek 4. Dwa bloki w wodospadzie. Źródło: f. Zapata.

Z kolei i₁(s) Wprowadź blok g₂(s), których odejście jest:

I₂(s) = x (s).G₁(S). G₂(S)

Procedura jest ważna dla N bloków kaskadowych:

I_N (s) = x (s). G₁(S).G₂(S) ... g_N(S)

Bloki równolegle

Na lewym schemacie sygnał x (s) bifurca do wejścia do bloków G₁(S) i g₂(S):

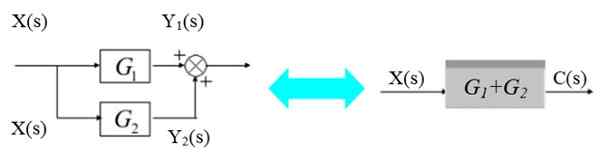Rysunek 5. Dwa bloki równolegle. Źródło: f. Zapata.

Odpowiednie sygnały wyjściowe to:

I₁(s) = x (s).G₁(S)

I₂(s) = x (s).G₂(S)

Sygnały te są dodawane w celu uzyskania:

C (s) = y₁(s) +₂(s) = x (s).[G₁(s) + g₂(S)]

Jak pokazano na prawym schemacie.

Przesuń konkurent w lewo

Lato może przesunąć się na lewo od bloku w następujący sposób:

Rysunek 6. Przesuń dodatek w lewo od bloku. Źródło: f. Zapata.

Po lewej stronie sygnał wyjściowy to:

C (s) = r (s). G (s) - x (s)

Równoważnie po prawej:

C (s) = [r (s) - x (s)/g (s)]]].G (s)

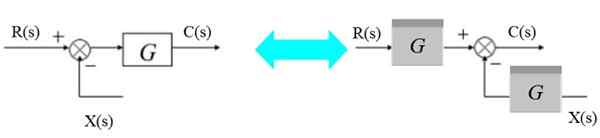
Przenieś prawo w prawo

Lato może poruszać się w prawo od bloku:

Rysunek 7. Przenieś wykres na prawo od bloku. Źródło: f. Zapata.

Po lewej stronie: [r (s) - x (s)].G (s) = C (s)

Może ci służyć: Archimedes Zasada: formuła, demonstracja, aplikacje

I po prawej:

R (s). G (s) - x (s).G (s) = C (s)

Przenieś punkt rozwidlenia od lewej do prawej

Aby wypierać punkt bifurkacji od lewej do prawej od bloku, wystarczy zauważyć, że wyjście C (S) po prawej to produkt X (S).G (s). Jak chcesz ponownie stać się x (s), jest on mnożony przez odwrotność g (s).

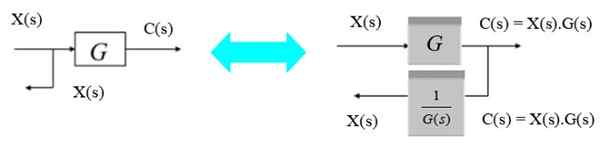Cyfra 8. Przesuń punkt odgałęziony od lewej do prawej. Źródło: f. Zapata.

Przenieś punkt rozwidlenia od prawej do lewej

Alternatywnie, punkt bifurkacji może poruszać się od prawej do lewej w następujący sposób:

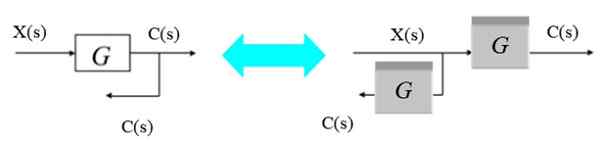Rysunek 9. Przesuń punkt odgałęziony od prawej do lewej. Źródło: f. Zapata.

Ponieważ wyjście bifurkacji chce uzyskać C (S), nowy blok G (S) jest po prostu przeplatany w punkcie rozwidlenia po lewej stronie pierwotnego bloku.

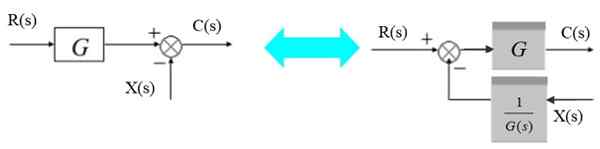
System z informacją zwrotną

W następującym systemie sygnał wyjściowy C (S) jest zasilający przez uległość po lewej:

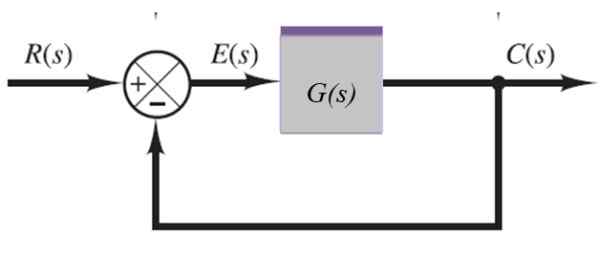Rysunek 10. System z informacją zwrotną. Źródło: f. Zapata.

C (s) = e (s).G (s)

Ale:

E (s) = r (s) -C (s)

Zastępowanie tego wyrażenia w poprzednim równaniu to: C (s) = [r (s) -C (s)]].G (s), z których można wyczyścić C (s):

C (s) + c (s).G (s) = r (s).G (s) → C (s). [1 + g (s)] = r (s).G (s)

C (s) = r (s).G (s) / [1 + g (s)]

Lub naprzemiennie:

C (s) / r (s) = g (s) / [1 + g (s)]]]

Graficznie po uproszczeniu jest:

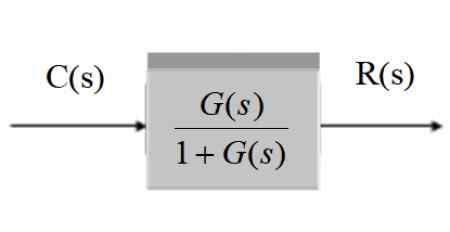Rysunek 11. Uproszczenie systemu z informacją zwrotną. Źródło: f. Zapata.

System z sprzężeniem zwrotnym i przetwornikiem

Przetwornik składa się z funkcji transferu H (-ów):

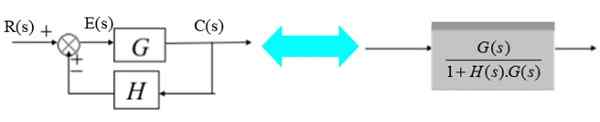Rysunek 12. System z sprzężeniem zwrotnym i przetwornikiem. Źródło: f. Zapata.

Na prawym schemacie sygnał wyjściowy C (y) to:

C (s) = e (s). G (s) z E (s) = r (s) - c (s).H (s)

Więc:

C (s) = [r (s) - c (s). H (s)]. G (s)

C (s) [1+ H (s).G (s)] = r (s).G (s)

Dlatego C (s) można usunąć przez:

C (s) = g (s).R (s) / [1+ H (s).G (s)]

A funkcją transferu będzie:

G (s) / [1+ H (s).G (s)]

Jak pokazano na uproszczonym prawym schemacie.

Rozwiązane ćwiczenia

Ćwiczenie 1

Znajdź funkcję transferu następującego systemu:

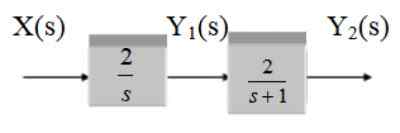Rysunek 13. Dwa systemy blokowe w wodospadzie. Źródło: f. Zapata.

Rozwiązanie

To dwa bloki kaskadowe, dlatego funkcja transferu jest iloczynem funkcji g₁ i g₂.

Musisz:

G₁ = 2/s

G₂ = 2 /(s+1)

Dlatego poszukiwana funkcja transferu jest:

G (s) = 4 / [s (s+1)]

Ćwiczenie 2

Zmniejsz następujący system:

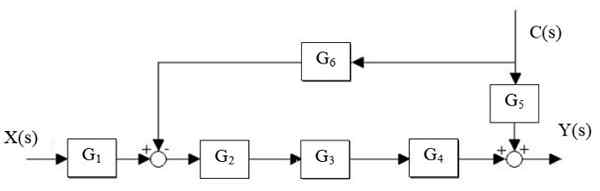Rysunek 14. Uproszczenie systemu. Źródło: f. Zapata.

Rozwiązanie

Najpierw kaskada G jest zmniejszona₂, G₃ i g_4, I równolegle g jest oddzielone₅ i g₆:

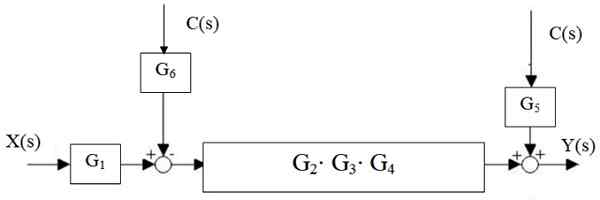Rysunek 15. Centralna redukcja wodospadu. Źródło: f. Zapata.

Następnie konkurent po lewej stronie bloku G₂ ⋅G₃ ⋅ g₄ Porusza się w prawo:

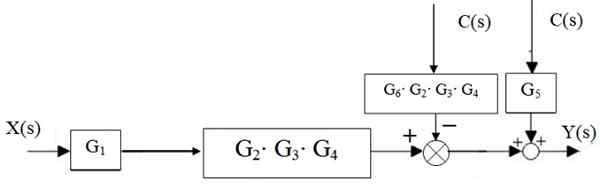Rysunek 16. Przeniesienie administratora. Źródło: f. Zapata.

Lata prawa są zredukowane do jednego, a także kaskadowe bloki:

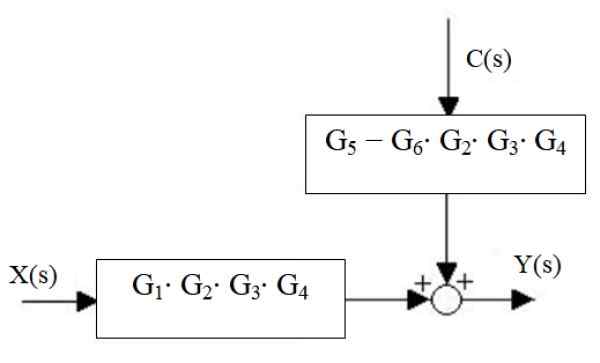Rysunek 17. Zmniejszenie nowego wodospadu i letnich prawej strony. Źródło: f. Zapata.

Wreszcie wyjście systemowe to:

I (s) = x (s) ⋅g₁⋅ g₂ ⋅G₃ ⋅ g₄ + C (s) ⋅ [g₅ - G₆ ⋅ g₂ ⋅G₃ ⋅ g₄]

Bibliografia

1. Alaydi, j. Kontrola schematu blokowego systemu. Odzyskane z:.Iugaza.Edu.$.
2. Bolton, w. 2006. Inżynieria kontrolna. 2. Wydanie. Alpha Omega.
3. CWALINSKY, J. Wprowadzenie do algebry blokowej systemu. Odzyskane z: cedengineering.com.
4. TatusemuchConnection. Schemat bloków. Wyzdrowiał: tatusemuch.com.
5. Ogata, k. 2010. Nowoczesna inżynieria kontroli. 5. Wydanie. osoba.