Znaki prawo

Wyjaśniamy prawo znaków, z ustalonymi przykładami i ćwiczeniami

Schemat ustawy o znakach

Jakie jest prawo znaków?

Znaki prawo Jest to zestaw reguł stosowanych w obliczeniach arytmetycznych i algebraicznych z liczbami rzeczywistymi do prawidłowego przypisania znaku do wyniku, gdy zaangażowane są zarówno kwoty dodatnie, jak i ujemne.

Istnieją odpowiednie zasady zgodnie z przeprowadzoną operacją: suma, odejmowanie, mnożenie i podział, które są najbardziej podstawowe, a także zasady objawów związanych z operacją wzmocnienia i składania.

W danej operacji, niezależnie od tego, czy ręcznie, czy z kalkulatorem, konieczne jest prawidłowe zastosowanie prawa znaków, aby zapewnić prawidłowy wynik, ponieważ tylko niewielka zmiana znaków znacząco zmienia ilości.

Prawo znaków dla każdej podstawowej operacji arytmetycznej i przypadki, które mogą się pojawić, są badane poniżej.

Prawo znaków w sumie

1) Jeśli liczby do dodania mają ten sam znak

Liczby są dodawane jak zwykle, a wynik jest dodawany do znaku liczb, niezależnie od tego, czy jest to pozytywne czy negatywne.

Ważne jest, aby pamiętać, że liczby dodatnie zwykle nie są przed znakiem, ale są pisane bezpośrednio. Z drugiej strony liczby ujemne są zapisane w nawiasach, szczególnie gdy są poprzedzone symbolem operacji arytmetycznej, aby uniknąć zamieszania.

Przykłady sum liczb o tym samym znaku:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (-10) + (−6) = −21

2) Jeśli liczby do dodania mają inny znak

Liczby są odjęte, a znak liczby, który ma największą wartość bezwzględną, jest dodawany do wyniku, czy to dodatni, czy ujemny.

Jako przykład, przeprowadzaj operację 5 + (-14). Ponieważ wartość bezwzględna (-14) jest większa niż wartość bezwzględna 5, 5 jednostek odejmuje się od 14, co daje 9, a wynik ten jest umieszczony znak ujemny:

Może ci służyć: pryzmaty i piramidy

5 + (−14) = −9

Więcej przykładów tej zasady zastosowanych do suma dwóch liczby różnych znaków to:

(-27) + 12 = −15

12 + (−7) = 5

Jeśli w operacji istnieją więcej niż dwa dodatki o różnych znakach, właściwość asocjacyjna kwoty:

(−20) + 9 + (−7) = [(−20) + 9] + (−7)

Operacja jest najpierw wykonywana w Pracete, która składa się z sumy dwóch liczb różnych znaków, dla których zastosowana jest opisana reguła: wynik jest odejmowany i znak liczby o najwyższej wartości bezwzględnej:

(−20) + 9 = −11

Operacja jest taka:

(−20) + 9 + (−7) = (−11) + (−7)

Teraz masz sumę dwóch liczb tego samego znaku, a następnie są one zwykle dodawane, a wynik jest umieszczony znak ujemny:

(−20) + 9 + (−7) = (−11) + (−7) = −18

Znaki zastępcze

Odejmowanie dwóch liczb jest zdefiniowane jako suma przeciwnego. Z kolei wręcz przeciwnie do liczby jest wymieniona liczba ze zmienionym znakiem. Na przykład przeciwieństwo 2 to (-2), przeciwieństwo (-5) wynosi 5 i tak dalej.

Mając to na uwadze, gdy masz odejmowanie dwóch liczb:

A - b

Po prostu przekształca się w sumę przeciwieństwa B:

A + ( - b)

I postępuj zgodnie z opisem w poprzedniej sekcji. Uwaga, aby umieścić znak + liczba ujemna go nie zmienia, ale bardzo ostrożnie, odwrotnie nie jest prawdą.

Gdy liczba „a”, która jest minuend, jest większa niż liczba „b”, która jest skradziona, działa jak w odjęciu liczb naturalnych. Nie ma problemu, ponieważ duża liczba jest odejmowana od mniejszej ilości:

Może ci służyć: nierówność trójkąta: demonstracja, przykłady, rozwiązane ćwiczenia

25 - 8 = 17

Z następującymi przykładami metoda dodawania przeciwnego do odejmowania jest bardzo wygodna:

(-5) - 24 = (-5) +( - 24) = - 29
32 - (−23) = 32 + 23 = 55

Prawo znaków w mnożenie

W ten sposób stosuje się prawo znaków mnożenia:

• Mnożąc dwie liczby tego samego znaku, wynik jest zawsze pozytywny.
• Produkt dwóch przeciwnych liczb znaków jest zawsze ujemny.

Podsumowanie reguły znaków dla mnożenia jest pokazane na obrazie:

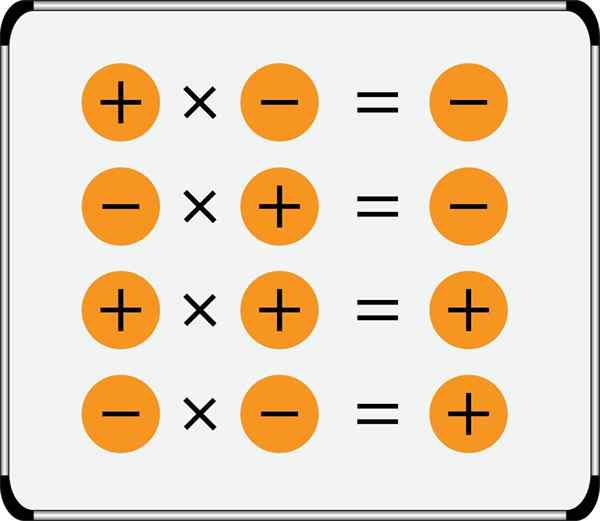
Zauważ, że liczby dodatnie mogą być napisane bez poprzedniego znaku, ale liczby ujemne zawsze mają go, ponadto dwa symbole arytmetyczne nigdy nie są pisane sobie, na przykład należy je oddzielać przez nawias:

Błędny: 3 × −4
Prawidłowy: 3 × (−4) = −12

(-5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270

Aby pomnożyć więcej niż dwie liczby, stosuje się właściwość asocjacyjną mnożenia, ponieważ kolejność czynników nie zmienia produktu, na przykład podczas przeprowadzania:

(-2) × (-14) × 16

Możesz pomnożyć pierwsze dwa czynniki lub dwa ostatnie, jeśli chcesz, a następnie pomnożyć wynik przez pozostały współczynnik. W takim przypadku dwa czynniki zostaną pomnożone po raz pierwszy po lewej:

[(−2) × (−14)] × 16

Produkt dwóch liczb ujemnych jest dodatni, a następnie (-2) × (-14) = 28 i pozostaje:

28 × 16 = 448

Prawo znaków w podziale

Jest to analogiczne do zasady znaków mnożenia:

• Stosunek dwóch liczb tego samego znaku jest zawsze dodatni.
• Dzieląc dwie inaczej liczby znaków, wynik jest zawsze ujemny.

Może ci służyć: różnica między okrągiem a obwodem (z przykładami)

Na przykład:

24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (-9) = −18
−216 ÷ (-6) = 36

Prawo znaków w wzmocnieniu i zgłoszeniu

Wykładnik numeru pisemnego to:

Do^N

Gdzie „A” jest podstawą, a „n” jest wykładnikiem. Dwa przypadki wyróżniają się, zgodnie z parytetem wykładnika:

Przypadek 1: A jest pozytywny

Gdy podstawa jest pozytywna, wynik jest pozytywny, niezależnie od tego, czy wykładnik jest równy, czy dziwny, jak w:

2³ = 8
3⁴ = 81

Przypadek 2: A jest negatywny

Oto dwa przypadki:

• Gdy wykładnik jest równy, wynik jest dodatni.
• Jeśli wykładnik jest dziwny, jest ujemny.

Przykłady

3² = 3 ∙ 3 = 9
2³ = 2 ∙ 2 ∙ 2 = 8
(-2)⁴ = (−2) ∙ (−2) ∙ (−2) ∙ (−2) = 16
(−3)³ = (−3) ∙ (−3) ∙ (−3) = −27

Operacje z grupowaniem symboli

Często pojawiają się oddzielne operacje z grupą symboli: nawiasy, wsporniki i klucze. Są one wyeliminowane od wewnątrz, biorąc pod uwagę następujące:

• Jeśli symbol grupowania jest poprzedzony znakiem dodatnim, można go usunąć bez zmiany znaków zawartości, na przykład: + (−3 + 5 - 1) = −3 + 5 - 1 = 1.
• Jeśli znak ujemny poprzedza symbol grupy, zostanie wycofany przez inwestowanie znaku treści, na przykład: - (−3 + 5 −1) = 3 - 5 + 1 = −1.
• W przypadku połączonych operacji sum, odejmowania, mnożenia i podziału, właściwości asocjacyjne i dystrybucyjne mogą być wykorzystane do wygody.

Rozwiązane ćwiczenia

a) 10 + 10

Rozwiązanie: 20

b) (-8) + (-3)

Rozwiązanie: -11

c) (3) + (-10) 

Rozwiązanie: -7

d) (5) x (-3)

Rozwiązanie: -15

e) (-10) x (-10)

Rozwiązanie: 100

f) (18) ÷ (-3)

Rozwiązanie: -6

G) (-10) ÷ (-2)

Rozwiązanie: 5

H) 4 - ( - 7 + 9)

Rozwiązanie: 4 - ( - 7 + 9) = 4 + 7 - 9 = 11– 9 = 2