Wyjaśnienie, formuła i jednostki, ćwiczenia, eksperymenty

Prawo kulombowskie Jest to prawo fizyczne, które reguluje interakcję między obiektami obciążonymi elektrycznie. Stwierdził to francuski naukowiec Charles Augustin de Coulomb (1736–1806), dzięki wynikach jego eksperymentów poprzez równowagę skrętną.

W 1785 r. Coulomb doświadczył niezliczonych czasów z małymi elektrycznie naładowanymi sferami, na przykład przynosząc lub odejście dwie kule, zmieniając wielkość jego obciążenia, a także znak. Zawsze obserwuj i starannie rejestrując każdą odpowiedź.

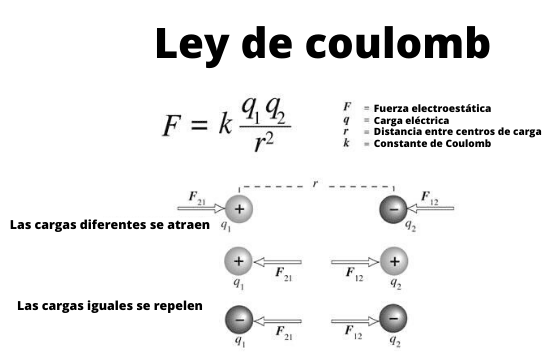
Rysunek 1. Program, który pokazuje interakcję między określonymi ładunkami elektrycznymi poprzez prawo Coulomba.

Te małe kule można uznać za obciążenia określone, to znaczy obiekty, których wymiary są nieznaczne. I spełniają, jak wiadomo od czasów starożytnych Greków, że obciążenia tego samego znaku są odpychane i przyciągane są obciążenia o różnych znakach.

Rysunek 2. Inżynier wojskowy Charles Coulomb (1736-1806) jest uważany za najważniejszego fizyka we Francji. Źródło: Wikipedia Commons.

Mając to na uwadze, Charles Coulomb znalazł następujące:

-Siła przyciągania lub odpychania między dwoma określonymi ładunkami jest bezpośrednio proporcjonalna do iloczyn wielkości obciążeń.

-Ta siła jest zawsze kierowana wzdłuż linii, która dołącza do ładunków.

-Wreszcie wielkość siły jest odwrotnie proporcjonalna do kwadratu odległości oddzielającej obciążenia.

[TOC]

Formuła i jednostki prawa kulombowskiego

Dzięki tym obserwacjom Coulomb stwierdził, że wielkość siły F Między dwoma konkretnymi zarzutami Q₁ I Q₂, oddzielono odległość R, Jest to matematycznie podane jako:

Ponieważ siła jest wielkością wektora, aby ją wyrazić, wektor jednostkowy jest całkowicie zdefiniowany R W kierunku linii, która łączy się do obciążeń (wektor jednostkowy ma wielkość równą 1).

Ponadto niezbędna stała proporcjonalności przekształcanie poprzedniego wyrażenia w równość nazywa się K_I lub po prostu k: stała elektrostatyczna albo COULOMB stała.

Wreszcie ustanawia się prawo kulombowskie dla obciążeń punktualnych, podane przez:

Siła, jak zawsze w międzynarodowym systemie jednostek, pojawia się w Newton (N). Jeśli chodzi o zarzuty, jednostka nazywa się Coulomb (c) na cześć Charlesa Coulomba, a wreszcie odległość R jest w metrach (M).

Uważnie obserwując poprzednie równanie, jasne jest, że stała elektrostatyczna musi mieć jednostki n.M² / C², W rezultacie uzyskać newtony. Wartość stały określono eksperymentalnie jako:

Może ci służyć: darmowe wektory: właściwości, przykłady, ćwiczenia

k_I = 8.89 x 10 ⁹ N.M² / C² ≈ 9 x 10 ⁹ N.M² / C²

Rycina 1 ilustruje interakcję między dwoma ładunkami elektrycznymi: gdy są tym samym znakiem, są odpychane, w przeciwnym razie przyciągają one.

Zauważ, że prawo Coulomba pasuje do trzeciego prawa lub prawa i reakcji Newtona, a zatem wielkości F₁ I F₂ Są takie same, adres jest taki sam, ale zmysły są odwrotnie.

Jak zastosować prawo Coulomba

Aby rozwiązać interakcje między ładunkami elektrycznymi, należy wziąć pod uwagę następujące:

- Równanie jest stosowane wyłącznie w przypadku obciążeń określonych, to znaczy obiektów obciążonych elektrycznie, ale bardzo małych wymiarów. Jeśli obciążone obiekty mają wymierne wymiary, konieczne jest podzielenie ich na bardzo małe obciążenia, a następnie dodać udział każdego z tych obciążeń, dla których wymagane są kompleksowe obliczenia.

- Siła elektryczna jest wielkością wektorową. Jeśli oddziałują więcej niż dwa ładunki, siła netto na obciążeniu Q_Siema Jest to podawane przez zasadę superpozycji:

F_Internet = F_i1 + F_I2 + F_i3 + F_i4 +… = ∑ F_IJ

Gdzie dolna indencja J Vale 1, 2, 3, 4 ... i reprezentuje każdy z pozostałych obciążeń.

- To zawsze musi być spójne z jednostkami. Najczęstsze jest praca ze stałą elektrostatyczną w jednostkach, jeśli musisz upewnić się, że obciążenia są w kulombowce, a odległości w metrach.

- Na koniec równanie jest stosowane, gdy obciążenia są w równowadze statycznej.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Na poniższym rysunku istnieją dwa obciążenia specyficzne +Q i +2q. Trzeci obciążenie punktualne -Q umieszcza się na P. Poproszono o znalezienie siły elektrycznej na tym obciążeniu ze względu na obecność pozostałych.

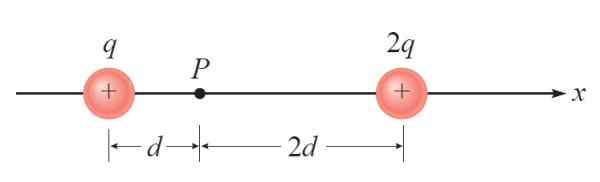Rysunek 3. Schemat dla roku rozstrzygnął 1. Źródło: Giambattista, a. Fizyka.

Rozwiązanie

Pierwszą rzeczą jest ustanowienie odpowiedniego systemu odniesienia, który w tym przypadku jest oś pozioma lub osi x. Pochodzenie tego systemu może być wszędzie, ale przez komfort zostanie umieszczony w P, jak pokazano na rysunku 4a:

Może ci służyć: Bethelgeuse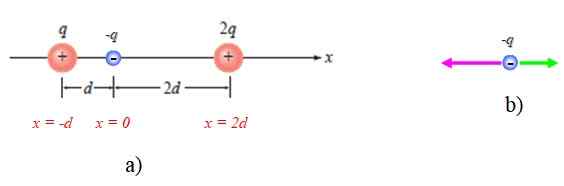Rysunek 4. Program na rok rozwiązany 1. Źródło: Giambattista, a. Fizyka.

Pokazuje się również schemat sił na -q, biorąc pod uwagę, że przyciąga je pozostałe dwa (ryc. 4B).

Zadzwońmy F₁ Do siły, która wykonuje obciążenie, które na obciążeniu -q są one skierowane wzdłuż osi x i wskazują w sensie negatywnym, dlatego:

Wektor jednostki w kierunku osi x X Z obwodowym akcentem w równaniu. Jest to powszechna notacja dla wektora jednostkowego. Mniej pojawia się znak, ponieważ siła F₁ Punkty w negatywnym znaczeniu osi.

Analogiczne jest obliczane F₂:

Zauważ, że wielkość F₂ To połowa F₁, Chociaż obciążenie jest podwójne. Aby znaleźć siłę netto, są one ostatecznie dodane wektorowo F₁ I F₂:

F_Internet = (-k + k/2).(Q² /D²) (X) N = - (k/2).(Q² /D²) (X) N

- Ćwiczenie 2

Dwa sferty polistyrenowe o równej masie m = 9.0 x 10^-8 kg mają to samo obciążenie dodatnie q i są zawieszone o długości jedwabnej o długości l = 0,98 m. Kule są oddzielone odległość d = 2 cm. Obliczyć wartość.

Rozwiązanie

Sytuacja stwierdzenia opisano na rycinie 5a.

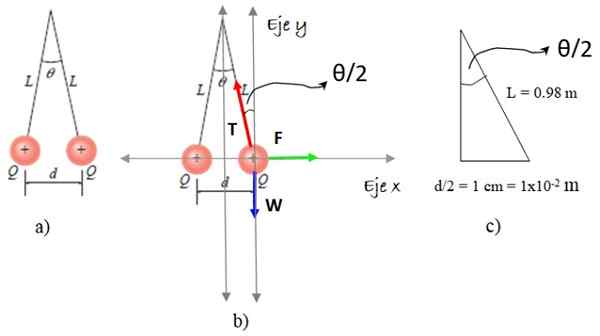Rysunek 5. Programy rozwiązywania ćwiczeń 2. Źródło: Giambattista, a. Fizyka /f. Zapata.

Wybraliśmy jedną z sfer i na nim rysujemy izolowany schemat ciała, który obejmuje trzy siły: waga W, Napięcie liny T i odpychanie elektrostatyczne F, Jak pojawia się na rycinie 5b. A teraz kroki:

Krok 1

Wartość θ/2 jest obliczana na podstawie trójkąta z rysunku 5C:

θ/2 = łuk (1 x 10^-2/0.98) = 0.585º

Krok 2

Następnie musisz zastosować drugie prawo Newtona i dopasować 0, ponieważ opłaty są w równowadze statycznej. Ważne jest, aby podkreślić to napięcie T Jest nachylony i ma dwa elementy:

∑f_X = -T.sin θ + f = 0

∑f_I = T.cos θ - w = 0

Krok 3

Oczyszczamy wielkość napięcia ostatniego równania:

Może ci służyć: dynamika: historia, jakie studia, prawa i teorie

T = w/ cos θ = mg/ cos θ

Krok 4

Wartość ta jest zastąpiona w pierwszym równaniu, aby znaleźć wielkość F:

F = t sin θ = mg (sin θ / cos θ) = mg. Tg θ

Krok 5

Jak f = k q² /D², Oczyszcza Q:

Zastępując wartości numeryczne dostarczone przez instrukcję, jest uzyskiwane:

Q = 2 × 10^-jedenaście C.

Eksperymenty

Sprawdzanie prawa Coulomba jest proste za pomocą równowagi skrętnej podobnej do tej używanej w jego laboratorium.

Istnieją dwie małe kule Saúco, z których jedna, jedna na środku równowagi, jest zawieszona z nici. Eksperyment polega na dotknięciu sfer Saúco pobranych z inną metalową kulą załadowaną obciążeniem Q.

Rysunek 6. Bilans skrętny Coulomba.

Natychmiast obciążenie jest rozkładane równo między dwiema sferami Saúco, ale potem, podobnie jak obciążenia tego samego znaku, odpychają. Siła, która powoduje skręt nici z nici i natychmiast odsuwa się od stałej kuli działa na zawieszoną kulę.

Następnie widzimy, że jest to kilka razy, aż do osiągnięcia równowagi. Następnie skrętka paska lub nici, która go trzyma.

Jeśli kule były pierwotnie na 0, teraz kula mobilna obróci kąt θ. Otaczając równowagę, w stopniach jest taśma absolwentna do pomiaru tego kąta. Po wcześniejszym określaniu stałej skrętu, wówczas siła odpychania i wartość obciążenia uzyskanego przez kulki Saúco można łatwo obliczyć.

Bibliografia

1. Figueroa, zm. 2005. Seria: Fizyka nauk i inżynierii. Tom 5. Elektrostatyka. Pod redakcją Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fizyka. Druga edycja. McGraw Hill.
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
4. Resnick, r. 1999. Fizyczny. Tom. 2. Wydanie trzecie. po hiszpańsku. Continental Editorial Company S.DO. c.V.
5. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Głośność 2.