Charakterystyka, typy i ćwiczenia zbieżne soczewki

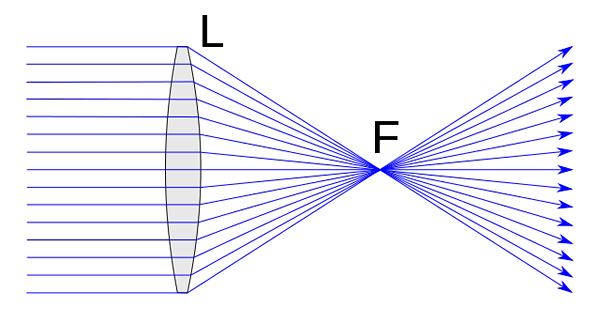
 Zbieżne soczewki Są tymi, które są grubsze w środkowej i cieńszej części na krawędziach. W konsekwencji koncentrują się (zbieżne) w jednym punkcie promienie światła, które wpływają na nich równolegle do osi głównej. Ten punkt nazywa się Focus lub Focus i jest reprezentowany z literą F. Soczewki zbieżne lub pozytywne formują się tak zwane prawdziwe obrazy obiektów.

Typowym przykładem zbieżnego soczewki jest szkło powiększające. Jednak często można znaleźć tego rodzaju soczewki na znacznie bardziej złożonych urządzeniach, takich jak mikroskopy lub teleskopy. W rzeczywistości podstawowym mikroskopem złożonym jest ten utworzony przez dwie zbieżne soczewki o niewielkiej odległości ogniskowej. Soczewki te są nazywane docelowym i oka.

Szkło powiększające, zbieżne soczewki. 

Zbieżne soczewki są używane w optyce dla różnych aplikacji, chociaż być może najbardziej znanym jest poprawienie wad widoku. W ten sposób są wskazane, aby się zajmować.

[TOC]

Charakterystyka

Zbieżne obiektyw. Chetvorno [CC0]

Zbieżne obiektywy mają funkcje serii, które je definiują. W każdym razie być może najważniejsze jest to, co już rozwinęliśmy w swojej definicji. Zatem soczewki zbieżne charakteryzują się przekształceniem przez fokus każdy promień, który wpływa na nich w kierunku równolegle do osi głównej.

Ponadto, w sposób wzajemny, każdy promień incydentu, który przekracza skupienie, jest załamany równolegle do osi optycznej soczewki.

Zbieżne elementy soczewek

W obliczu badania ważne jest, aby wiedzieć, jakie elementy stanowią soczewki w szczególności soczewki.

Ogólnie rzecz biorąc, nazywa się to środkiem optycznym soczewki do tego stopnia, że ​​każdy promień, który przechodzi przez niego.

Główna oś jest linia, która dołącza do centrum optycznego i głównym skupieniem, które już skomentowaliśmy, że jest reprezentowana z literą F.

Może ci służyć: Ton: Transformacje, równoważniki i ćwiczenia rozwiązane

Nazywa się to głównym skupieniem do punktu, w którym znajdują się wszystkie promienie, które wpływają na soczewkę równolegle do osi głównej.

Odległość między środkiem optycznym a ostrością nazywana jest odległością ogniskową.

Centra krzywizny są definiowane jako centra kulek, które tworzą soczewkę; Z drugiej strony, radiotelefatury krzywizny radia kulek, które powodują soczewkę.

I wreszcie nazywa się płaszczyzną optyczną do środkowej płaszczyzny soczewki.

Tworzenie obrazów w zbieżnych soczewkach

W obliczu tworzenia obrazów w zbieżnych obiektywach, należy wziąć pod uwagę serię podstawowych zasad, które zostały wyjaśnione.

Jeśli promień wpływa na soczewkę równolegle do osi, wschodzący promień zbiega się na obrazie ostrości. Odwrotnie, jeśli promień incydentu przekroczy ostrość obiektu, błyskawica wyłania się w kierunku równolegle do osi. Wreszcie promienie, które przekraczają centrum optyczne, są załamane bez doświadczania odchylenia.

W konsekwencji w zbieżnym obiektywach możesz podać następujące sytuacje:

- Że obiekt znajduje się w odniesieniu do płaszczyzny optycznej w odległości większej niż dwukrotnie większa niż odległość ogniskowa. W takim przypadku występujący obraz jest prawdziwy, odwrócony i mniejszy niż obiekt.

- Że obiekt znajduje się w odległości od płaszczyzny optycznej równej dwukrotnie większej odległości. Kiedy tak się dzieje, uzyskany obraz jest prawdziwym, odwróconym obrazem i tego samego rozmiaru co obiekt.

- Że obiekt znajduje się w odległości od płaszczyzny optycznej między razu i dwa razy większą od odległości ogniskowej. Więc wytwarzany jest obraz jest prawdziwy, odwrócony i większy niż oryginalny obiekt.

- Że obiekt znajduje się w odległości od płaszczyzny optycznej niższej niż odległość ogniskowa. W takim przypadku obraz będzie wirtualny, bezpośredni i większy niż obiekt.

Może ci służyć: szok magnetyczny: jednostki, wzory, obliczenia, przykłady

Rodzaje zbieżnych soczewek

Istnieją trzy różne rodzaje zbieżnych soczewek: soczewki Biconvex, soczewki Planoconvex i soczewki z konparzonki.

Soczewki Biconvex, jak sama nazwa wskazuje, składają się z dwóch wypukłych powierzchni. Tymczasem Planoconvexas mają płaską powierzchnię i kolejną wypukłą. I wreszcie, soczewki konpiokonvex są składane przez lekko wklęsłą powierzchnię i kolejną wypukłą.

Różnica z rozbieżnymi soczewkami

Zbieżne obiektyw. FIR0002 (Talk) (przesyłanie) [CC BY-SA 3.0 (http: // creativeCommons.Org/licencje/by-sa/3.0/]]

Z drugiej strony rozbieżne soczewki różnią się od zbieżności, ponieważ grubość maleje od krawędzi w kierunku środka. Zatem, w przeciwieństwie do tego, co się stało z zbieżnymi, w tego typu soczewkach promienie światła, które wpływają równolegle do osi głównej. W ten sposób tworzą tak zwane wirtualne obrazy obiektów.

W optyce soczewki rozbieżne lub negatywne, jak są również znane, są używane głównie do skorygowania krótkowzroczności.

Równania Gaussa cienkich soczewek i zwiększonej soczewki

Zasadniczo rodzaj badanych soczewek to te zwane cienkimi soczewkami. Są one zdefiniowane jako te, które mają niewielką grubość w porównaniu z krzywizną powierzchni, które je ograniczają.

Ten typ soczewki można zbadać za pomocą równania Gaussa i równaniem, które pozwala określić wzrost soczewki.

Równanie Gaussa

Równanie Gaussa cienkich soczewek służy do rozwiązania wielu podstawowych problemów optycznych. Stąd jego wielka waga. Twoje wyrażenie jest następujące:

1/f = 1/p +1/q

Gdzie 1/ f jest tak zwana moc soczewki, a F jest odległością ogniskową lub odległością od środka optycznego do focam. Jednostką miary mocy soczewki jest diopter (d), wynoszącym 1 d = 1 m^-1. Ze swojej części, p i q są odpowiednio odległością, z jaką obiekt i odległość, na którą obserwuje się jego obraz.

Może ci służyć: teoria Wielkiego Wybuchu: cechy, etapy, dowody, problemy

Zwiększony obiektyw

Boczny wzrost cienkiej soczewki uzyskuje się z następującym wyrażeniem:

M = - Q / P

Gdzie m jest wzrostem. Z wartości wzrostu można wywnioskować szereg konsekwencji:

Tak | M | > 1, rozmiar obrazu jest większy niż rozmiar obiektu

Tak | M | < 1, el tamaño de la imagen es menor que el del objeto

Jeśli m> 0, obraz jest odpowiedni i po tej samej stronie soczewki co obiekt (wirtualny obraz)

tak m < 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)

Ćwiczenie rozwiązane

Ciało znajduje się metr od zbieżnego obiektywu, który ma odległość ogniskową 0, 5 metrów. Jaki będzie obraz ciała? Jak daleko znajdziesz?

Mamy następujące dane: p = 1 m; F = 0,5 m.

Zastępujemy te wartości w równaniu Gaussa cienkich obiektywów:

1/f = 1/p +1/q

I pozostaje następujące:

1/0,5 = 1 + 1/q; 2 = 1 + 1/q

Oczyszczamy 1/q

1/q = 1

Aby następnie wyczyścić Q i uzyskać:

Q = 1

Stamtąd zastępujemy w równaniu wzrostu w obiektywu:

M = -q / p = -1 / 1 = -1

Dlatego obraz jest prawdziwy od q> 0, odwrócony, ponieważ m < 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.

Bibliografia

1. Światło (n.D.). W Wikipedii. Pobrano 18 marca 2019 r.Wikipedia.org.
2. Lekner, John (1987). Teoria odbicia, fal elektromagnetycznych i częściowych. Skoczek.
3. Światło (n.D.). W Wikipedii. Pobrano 20 marca 2019 r. Z.Wikipedia.org.
4. Obiektyw (n.D.). W Wikipedii. Pobrano 17 marca 2019 r.Wikipedia.org.
5. Obiektyw (optyka). W Wikipedii. Pobrano 19 marca 2019 r. Z.Wikipedia.org.
6. Acts, Eugene (2002). Optyka (Wydanie 4.). Addison Wesley.
7. Tupler, Paul Allen (1994). Fizyczny. Wydanie trzecie. Barcelona: odwróciłem.