Homologiczne strony

Wyjaśniamy, jakie są homologiczne strony, wraz z rozwiązaniem przykładów i ćwiczeń

Jakie są homologiczne strony?

Homologiczne strony Na dwóch płaskich postaciach geometrycznych są te, które odpowiadają sobie nawzajem, zachowując podobieństwo. Na przykład prawa ręka osoby jest homologiczna z prawą ręką innej osoby.

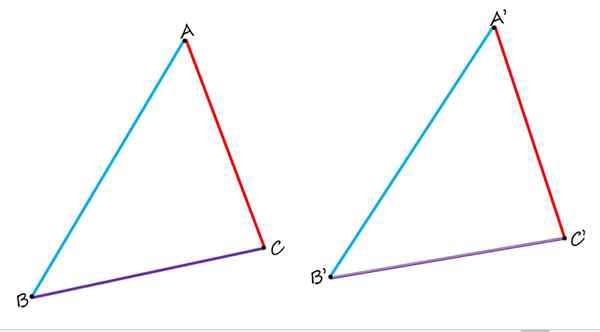
W płaskiej geometrii istnieją nie tylko homologiczne strony, ale także wierzchołki i kąty homologiczne. Aby to zobaczyć, rozważ następującą liczbę, która składa się z dwóch identycznych trójkątów ABC i A'B'C:

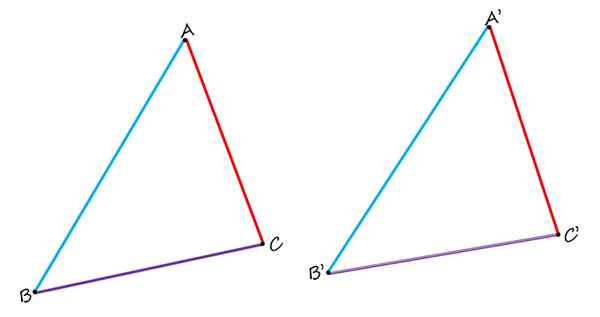W dwóch pokazanych identycznych trójkątów AB i A'B ', są homologiczne, a także boki BC i B'C' oraz AC i A'C '. Źródło: f. Zapata.

Podczas ich porównywania wyraźnie obserwuje się, że boki ab i a'b 'na niebiesko są homologiczne, ponieważ zajmują podobną pozycję w każdym trójkącie. Boki BC i B'C w fioletach są również homologiczne. I wreszcie, czerwona strona prądu przemiennego jest homologiczna z boku a'c '.

Wyjaśnienie

Z wyżej wymienionych wynika z tego, że homologiczne strony to te, które zajmują tę samą względną pozycję w postaci w ten sam sposób. Na poprzednim obrazie zastosowano dwa identyczne trójkąty do pokazania pomysłu, ale może to łatwo uogólnić inne płaskie liczby geometryczne, utworzone przez kolejne strony, które zamykają.

Te liczby są nazywane wielokąty. Na przykład trójkąty i czworobok to wielokąty odpowiednio 3 i 4.

Koncepcja boków homologicznych jest ważna, ponieważ pozwala na zdefiniowanie kryteriów podobieństwa między wielokątami, co będzie widać wkrótce. Podobne postacie mają dokładnie ten sam kształt i zachowują identyczną proporcję między swoimi bokami, nawet jeśli nie mają tego samego rozmiaru.

I chociaż do tej pory odniesiono tylko płaskie postacie, istnieją również podobne liczby w trzech wymiarach. Można je łatwo obserwować na półkach w supermarkecie, gdy ten sam produkt jest sprzedawany w identycznych pojemnikach, ale o innym rozmiarze.

Może ci służyć: logika matematyczna

Innymi słowami, które są używane zamiennie w geometrii w odniesieniu do homologicznych stron w rysunkach geometrycznych, to: odpowiednie strony, odpowiednie strony i równoważne strony.

Homologiczne wierzchołki i kąty

Podobnie jak w przypadku boków, definiowane są również homologiczne wierzchołki, które łączą pary homologicznych stron. Na przykład wierzchołki a i „z poprzedniej figury są homologiczne. Podobnie pary wierzchołków B i B 'i C i C' są homologiczne.

Wreszcie, homologiczne kąty zajmują tę samą względną pozycję na liczbach. Wierzchołki kątów homologicznych są z kolei homologiczne.

Aby zilustrować ten pomysł, weź kąt między niebieskimi i fioletowymi stronami lewego trójkąta, który można oznaczyć jako ∠ABC. Ten kąt ma swój odpowiednik pod kątem ∠A'B'C ', od trójkąta do prawej.

Wierzchołek tego kąta jest B, który, jak wskazano wcześniej, jest odpowiednikiem z B ', a pozostałe dwie pary homologicznych kątów pokazanych trójkątów to:

• ∠BCA i ∠B'C'a '
• ∠CAB i ∠C'A'B '

Podobieństwo wielokątów

Aby dowolne dwa wielokąty były podobne, należy spełnić następujące warunki:

• Wszystkie pary homologicznych kątów mają tę samą miarę
• Jego pary homologicznych stron są proporcjonalne.

Dwa warunki muszą być spełnione jednocześnie, aby zapewnić podobieństwo. Natychmiast obserwuje się, dlaczego.

Na poniższym rysunku istnieją dwa czworobok, które oczywiście nie są podobne. Wynika to z faktu, że pierwszy status tygodnia jest spełniony, ale drugi nie:

Dwa czworokątne, które nie są podobne, chociaż ich homologiczne kąty mają równą miarę. Źródło: f. Zapata.

Podczas gdy na liczbach ich pary homologicznych kąty mają tę samą miarę, ponieważ wszystkie są prostymi kątami (mierzą 90º), liczby nie są podobne, ponieważ ich pary boków nie są proporcjonalne.

Może ci służyć: funkcja iniekcyjna: z czego składa się, do czego jest i przykłady

Z drugiej strony te dwa czworobory mają homologiczne strony o równej miarę, ale homologiczne kąty nie mierzą tego samego. Dlatego liczby nie są podobne.

Dwa czworobok z homologicznymi stronami tej samej miary, ale z różnymi kątami wewnętrznymi, dlatego nie są to podobne liczby. Źródło: f. Zapata.

Powód podobieństwa

Jeśli dwie liczby są podobne, iloraz między homologicznymi stronami jest taki sam i jest nazywany Powód podobieństwa.

Oznaczając boki jednej z postaci, takich jak A, B, C, D ... i odpowiednie z drugiej postaci, takie jak A ', B', C ', D

Obwody i obszary o podobnych postaciach

Wskaźnik podobieństwa pozwala na uzyskanie zależności między obwodami, obszarami i objętościami dwóch podobnych liczb.

Przyczyna obwodu dwóch podobnych liczb

Obwód P wielokąta jest zdefiniowany jako suma wszystkich jego stron. Jeśli masz figurę, której boki to „, b ', c', d '..., jej obwód p' to:

P '= a' + b ' + c' + d '.. .

Jeśli inny wielokąt jest podobny do tego, a jego boki to A, B, C, D ..., spełniło się, że:

I dlatego:

A = r ∙ a '

Możesz potwierdzić to samo dla innych stron tej liczby. Tak więc obwód P jest wyrażany jako:

P = A + B + C + D .. . = r ∙ a ' + r ∙ b' + r ∙ c ' + r ∙ d' +…

Ponieważ „R” jest wspólnym czynnikiem dla wszystkich uzależnionych, związek między P i P 'wynosi:

P = r ∙ p '

Oznacza to, że przyczyna obwodów między dwoma podobnymi wielokątami jest równa przyczyna podobieństwa.

Powód obszarów dwóch podobnych liczb

Jeśli dwie podobne liczby mają odpowiednio obszary a i a ', są one powiązane przez:

Może ci służyć: ćwiczenia prześwitu formuły

A = r²∙ A '

Gdzie „r” jest przyczyną podobieństwa figur.

Współczynnik objętości dwóch podobnych liczb

Są to dwie podobne trzy wymiarowe postacie, których objętości są odpowiednio V i V '. Relacja między nimi, poprzez „R” to:

V = r³∙ V '

Przykłady

Plany

Części ziemi, zakład budynku, a nawet odzieży, na mniejszą skalę na arkuszu papieru można reprezentować. Plany mają tę zaletę, że można zabrać ze sobą i łatwo dokonywać odpowiednich modyfikacji.

Mapy

Są to zwykle reprezentacje w płaszczyźnie dużego obszaru ziemi, od wioski po kontynenty. Są również wytwarzane na określoną skalę.

Mają wiele aplikacji i istnieje wiele rodzajów. Na przykład za pośrednictwem mapy teren można opisać, a gdy znajduje się on w określonym punkcie, ustalona jest najlepsza trasa do tego punktu do drugiego.

Modele

Są to trzy -wymiarowe reprezentacje w skali obiektów, takich jak samochody, budynki i konstrukcje w ogóle.

Ćwiczenie rozwiązane

Następujące wartości odpowiadają bokom kilku podobnych trójkątów. Znajdź powód podobieństwa i wartości „x” i „y”:

Trójkąt 1: 5, 8, 10

Trójkąt 2: 150, x, y

Rozwiązanie

Powodem podobieństwa jest iloraz:

R = 150/5 = 30

Dlatego:

x = 30 × 8 = 240

y = 10 × 30 = 300