Matematyka

Interpolacja liniowa

Wyjaśniamy, jakie jest interpocja liniowa, jej wzory, jak je robić, z ustalonymi przykładami i ćwiczeniami

Co to jest interpolacja liniowa?

Interpolacja liniowa Polega na oszacowaniu lokalizacji punktu w przedziale numerycznym, zakładając, że ekstremalne wartości wspomnianego przedziału są zjednoczone przez linię. Znana równanie tej linii można zlokalizować nieznany punkt.

Pomysł jest schematyzowany na poniższym rysunku, który pokazuje podejście do wykresu funkcji między punktami A i B. Zakładając, że punkty te są bliskie, możliwe jest przybliżenie krzywej, która łączy je przez linię, a tym samym znajdowanie punktów pośrednich.

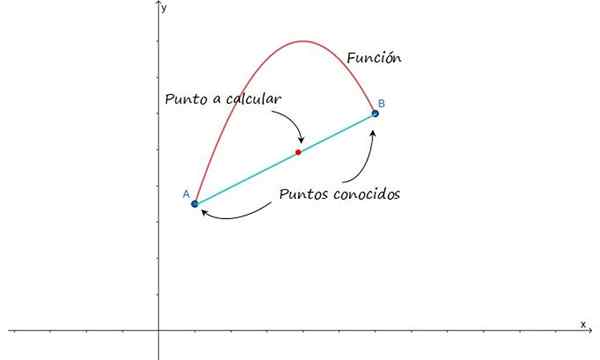Rysunek 1.- Aby dokonać liniowej interpolacji między punktami A i B, należy założyć, że są one połączone linią . Źródło: f. Zapata.

Możesz także przybliżyć krzywą, która łączy punkty podane za pomocą funkcji kwadratowej lub innej wielomianowej. Jednak linia ma tę zaletę, że jego matematyczna prostota, więc jest łatwa w obsłudze, chociaż jest najprostszą interpolacją ze wszystkich, możliwe jest, że wynik nie jest tak precyzyjny, jak ten uzyskany przy użyciu innych funkcji.

Formuły

Istnieją dwa punkty współrzędnych [x_albo, f (x_albo)] i [x₁, f (x₁)] wśród których jest punkt [x, g (x)], którego współrzędne są pożądane.

Pierwszy krok polega na dołączeniu do znanych punktów przez segment linii, na którym można znaleźć współrzędne punktu A.

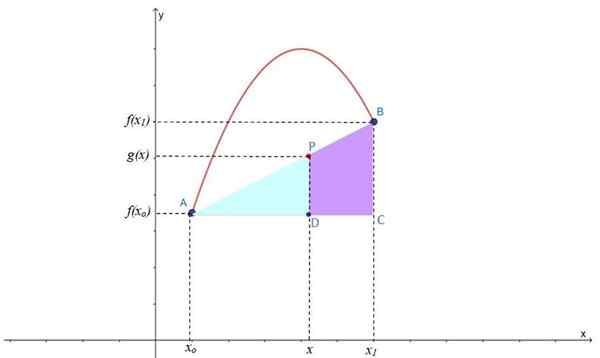Rysunek 2.- Interpolacja liniowa w celu znalezienia punktu P na linii interpoczencyjnej G (x), znajdującej się między punktami A i B F (x). Źródło: f. Zapata.

Jak widać, powstają dwa prostokąty: ABC i APD, które mają również ostry kąt, więc są to podobne trójkąty, do których można zastosować twierdzenie Thales:

Może ci służyć: geometria analityczna

$\fracADAC=\fracAPAB=\fracPDBC$ Zastępując miarę segmentów zgodnie z wykresem, uzyskuje się następującą zależność:

$\fracx-x_ox_1-x_o=\fracg(x)-f(x_o)f(x_1)-f(x_o)$ Stamtąd przechodzimy do wyczyszczenia G (x):

$g(x)=f(x_o)+\left [\fracf(x_1)-f(x_o)x_1-x_o \right ]\left ( x-x_o \right )$ Powołanie:

F₁(X₁) = y₁ ; F_albo(X_albo) = y_albo; g (x) = y

Górne równanie jest przekształcane w:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

Zakres błędów

Gdy funkcja zbliża się z tą metodą, poziom błędu jest podawany przez wartość bezwzględną różnicy między funkcją F (x) a linią interpolacyjną G (x):

Błąd = │f (x) - g (x) │

Jak dokonać interpolacji liniowej?

Przeprowadzenie interpolacji liniowej jest bardzo proste, wystarczy wykonać te kroki:

Krok 1

Określ nieznany punkt P (x, y).

Krok 2

Ustal dwa punkty, które ograniczają przedział, w którym znajduje się wartość do obliczania, to znaczy punktów (x x_albo,I_albo) i (x₁, I₁).

Krok 3

Wymień wszystkie wartości w równaniu:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

I oblicz wynik.

Przykłady interpolacji liniowej

Przykład 1

Chcesz znaleźć przybliżoną wartość LN 3 do interpolacji liniowej, biorąc pod uwagę następujące wartości:

LN 2 = 0.693147 i LN 4 = 1.386294

Porównaj wynik z wartością LN 3 uzyskaną przez kalkulator i określ popełniony margines.

Krok 1

Aby znaleźć przybliżoną wartość LN 3, musisz kontynuować sposób: Po pierwsze, nieznane jest ustalone, czyli y = ln 3, obok odpowiedniej wartości „x”: x = 3. To jest punkt, który chcesz obliczyć: (3, LN 3).

Krok 2

Następnie musisz ustalić punkty graniczne interwału ze znanymi wartościami. Poproszono o to z kolejnymi kilkoma punktami:

Dolny limit: [x_albo = 2; I_albo = ln 2 = 0.693147]
Górny limit: [x₁ = 4; I₁ = ln 4 = 1.386294]
Krok 3

Wartości określone w krokach 1 i 2 są starannie zastępowane w równaniu, aby wygenerować wynik podejścia do LN 3:

Może ci służyć: ile rozwiązań ma równanie kwadratowe?

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln\: 2+\left [\fracln4-ln24-2 \right ]\left (3-2 \right )$
$ln\: 3= 0.693147+\left [\frac1.386294-0.6931474-2 \right ]\left (3-2 \right )=1.039721$ Prawdziwa wartość LN 3 uzyskana przez kalkulator to:

LN 3 = 1.098612

A margines błędu wynosi:

Błąd = │1.098612 - 1.03971 │ = 0.059

Procentowy błąd interpolacji jest obliczany poprzez podzielenie błędu między rzeczywistą wartością LN3 i mnożeniem przez 100 %:

Błąd procentowy = (prawdziwy błąd/wartość) × 100 = (0.059/1.098612) × 100% = 5.4%

Przykład 2

Teraz chcesz znaleźć przybliżoną wartość LN 3 przez interpolację liniową, znane te dwie wartości:

LN 2.5 = 0.916291 i LN 3.5 = 1.252763

Określ także odpowiedni błąd i porównaj z wynikami poprzedniego przykładu.

Krok 1

Znowu nieznany punkt to:

y = ln 3, x = 3

Krok 2
Dolny limit: [x_albo = 2.5; I_albo = y_albo = ln 2.5 = 0.916291]
Górny limit: [x₁ = 3.5; I₁ = ln 3.5 = 1.252763]
Krok 3

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln \: 2.5+\left [\fracln\: 3.5-ln \: 2.53.5-2.5 \right ]\left (3-2.5 \right )=1.084527$ Badanie wartości oferowanej przez kalkulator:

LN 3 = 1.098612

Poziom błędu jest określany w tym przypadku, co wynika:

Błąd = │1.098612 - 1.084527 │ = 0.014

Błąd procentowy w tym przypadku wynosi ≈ 1.3 %. W porównaniu z poziomem błędu przykładu 1, nowa wartość jest bardziej precyzyjna, ponieważ przedział wybrany na interpolarne jest niższe.

Rozwiązane ćwiczenia

Ćwiczenie 1

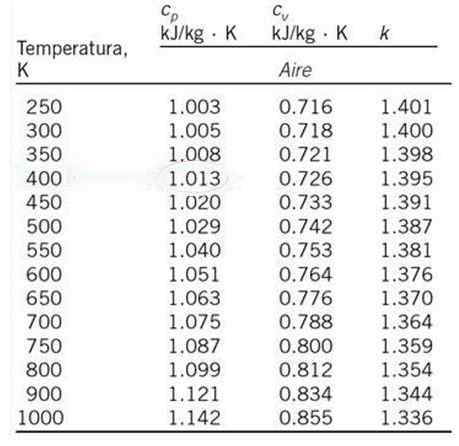
Oblicz, przez interpolację liniową, ciepło właściwe powietrza przy stałym ciśnieniu C_P i temperatura 530 K, zaczynając od tabeli wartości pokazanych poniżej.

Rozwiązanie

W rozwiązywaniu wielu problemów często poszukiwana wartość nie wydaje. Alternatywą jest wybranie wartości najbliższej pożądanej, ale wiele razy interpolacja liniowa wystarczy, aby znaleźć znacznie lepsze podejście.

Może ci służyć: oznaki grupowania

Wartość C_P 530 K nie pojawia się w dołączonym tabeli, ale interpolacja liniowa może być wykonana z odpowiednimi cieplami właściwymi przy 500 K i 550 K, które są temperaturami najbliższymi 530 K i których ciepło specyficzne pojawiają się w pokazanym tabeli.

Odpowiednie ciepło właściwe dla tych temperatur to:

T_albo = 500 K; C_PO = 1.029 kJ /kg ∙ k

T₁ = 550 K; C_P1 = 1.040 kJ /kg ∙ k

A nieznany jest punkt (500k, c_P)

Zastąpienie wzoru liniowego interpolacji podanej powyżej, z t na scenie zmiennej „x” i c_P Zamiast „y” masz:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$c_p= c_po+\left [\fracc_p1-c_poT_1-T_o \right ]\left (T-T_o \right )$

$c_p= 1.029+\left [\frac1.040-1.029550-500 \right ]\left (530-500 \right )\frackJkg\cdot K=1.03536\frackJkg\cdot K$

Ćwiczenie 2

Obciążenie zastosowane do sprężyny (w Kilopondios) wytwarza następujące wydłużenia (w milimetrach) zgodnie z pokazaną tabelą:

Oblicz wydłużenie, gdy obciążenie wynosi 12.6 kp.

Rozwiązanie

Niech i wartość wydłużenia poszukiwanego, gdy obciążenie wynosi c = 12.6 kp. Nieznany punkt jest (12.6, y), który jest jednym z punktów:

C_albo = 10 kp; I_albo = 105 mm

C₁ = 15 kp; I₁ = 172 mm

Pozostaje tylko na zastąpienie wartości w równaniu:

$C= 105+\left [\frac172-10515-10 \right ]\left (12.6-10 \right )\: mm=139.84\: mm$ Proponowane ćwiczenie

Oblicz ciepło właściwe do stałej objętości dla temperatury 727 K, przy użyciu interpolacji liniowej i tabeli papierów wartościowych ćwiczeń rozstrzygniętych 1.

Bibliografia

Akademia Rafa Vilchez. Jak przeprowadzić interpolację liniową. Odzyskane z: Acadraafavilchez.com
Chapra, s. 2007. Metody numeryczne dla inżynierów. 5. Wydanie. McGraw Hill.
Khan academy. Matematyka interpolacji liniowej. Odzyskane z: Khanacademy.org.
Życie edukacyjne. Liniowy wzór interpolacji. Odzyskane z: TheeducationLife.com
X-inżynier. Interpolacja liniowa i ekstrapolacja za pomocą kalkulatora. Odzyskany z: X-inżynier.org.

Interpolacja liniowa

Co to jest interpolacja liniowa?

Formuły

Zakres błędów