Równość matematyczna

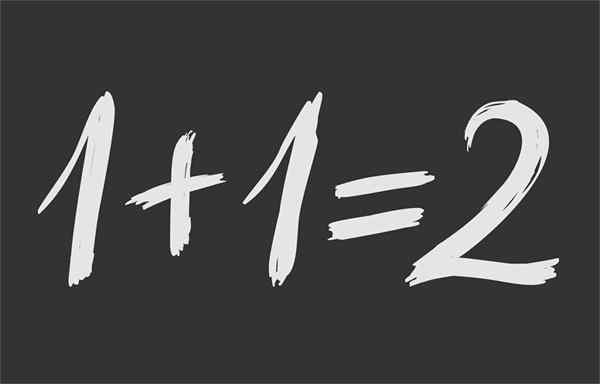Rysunek 1.- Równość matematyczna zapewnia, że ​​1 + 1 jest tym samym 2

Co to jest równość matematyczna?

Matematyczna równość zapewnia, że ​​dwa wyrażenia są takie same lub różne, są one całkowicie równoważne. Te wyrażenia mogą być różnorodną naturą, na przykład liczbami, literami, które symbolizują ilości lub wielkości, kombinacje liczb i liter, macierzy i inne.

Symbol użyty do oznaczenia równości w języku matematycznym jest symbol dwóch linii równoległych i poziomych, które w drukowanym tekście jest dobrze znanym symbolem „=”. Na przykład, jeśli masz trzy jabłka, możesz napisać następującą równość:

Liczba jabłek = 3

Wyrażenie „Liczba jabłek” jest członkiem lewej, a numer 3 jest członkiem po prawej stronie równości.

Ponieważ możliwe jest pisanie ilości liczbowych na różne sposoby, równość jest używana do ich oznaczenia. Biorąc konkretny przypadek, aby zilustrować ten punkt, istnieje kilka sposobów napisania numeru 4, oprócz najbardziej oczywistych, jakie to 4 = 4, następujące można zapisać, poprzez równość matematyczną:

2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
2² = 4

Pokazana tutaj równość jest prawdziwa, ale równość może nie być, na przykład 10 + 5 = 20 jest fałszywa, ponieważ 10 + 5 = 15.

Z pewnością czytelnik zna inne sposoby napisania numeru 4. Zauważ, że wyrażenia po każdej stronie równości mogą być liczbami, słowami, literami symbolizującymi ilości lub inne symbole, na przykład:

x + 1 = 7
Do²B - 1 = xy
f (x) = 2x²

Matematycy nie zawsze używali symbolu równości, więc stare traktaty matematyczne były bardzo obszerne.

Jest przypisywany matematykowi i doktorowi Robertowi Remember (1510-1558), urodzonym w Walii, stworzeniu symbolu równości „=”, tak znanego dziś wszystkim. Pamiętaj, najwyraźniej zmęczony pisaniem przez cały czas wyrażenia „jak” w jednym ze swoich traktatów matematycznych, postanowił skrócić na swoim miejscu, krewne równoległe paski.

Może ci służyć: Pentagonowy pryzmat: Charakterystyka, części, wierzchołki, krawędzie, objętość

Właściwości równości matematycznej

Poniższe właściwości pozwalają poprawnie działać z równością matematyczną. Są aksjomatyczne, więc nie wymagają demonstracji:

1.- Właściwość refleksyjna

Ta nieruchomość stwierdza, że ​​każda kwota jest równa sobie. W szczególności, ponieważ dowolna liczba jest równa sobie, można zapisać równe:

5 = 5

36.35 = 36.35

Jeśli kwota jest dosłowna lub jest to połączenie liter i liczb, jest również równa sobie:

3x = 3x

Do²pne^-1 = a²pne^-1

2.- Własność symetrii

Kwoty lub członkowie po obu stronach równości można wymieniać bez utraconej ważności. To znaczy, jeśli to, co jest po lewej stronie symbolu „=”, jest napisane po twojej prawej stronie, a to, co jest po prawej stronie, jest umieszczone po lewej, jest to ta sama równość.

Na przykład wyrażenie 5 + 2 = 7 jest równoważne z tym: 7 = 5 + 2. W ten sam sposób:

12 + 8 = 20; 20 = 12 + 8

x + 1 = 3; 3 = x + 1

x - z = y; y = x - z

3.- Przejazna własność

Ta właściwość odnosi się do równoważności równości. Jeśli dwie równości mają wspólnego członka, są one również takie same, ponieważ ogólnie:

Jeśli „x = y” i „y = z”, to x = z

Aby zilustrować tę właściwość, rozważ te dwie równości numeryczne: 2 + 2 = 4 i 6 - 2 = 4. Ponieważ oba są równe 4 (mają wspólnego członka), wówczas można zapisać następujące, bez utraty ważności:

2 + 2 = 6 - 2

Kolejny przykład, tym razem z literami:

Tak x + 1 = 5

I

A - B = 5

Więc:

x+1 = a - b

4.- Nieruchomość anulowania

Równość nie jest zmieniana, jeśli u obu członków istnieje taka sama kwota, która dodaje (lub odejmuje) i postanawia to wyeliminować lub anulować. To jest właściwość anulowania sumy.

Weźmy jako przykład następującą równość liczbową, w której 10 pojawia się zarówno w członku prawej, jak i w tym po lewej:

Może ci służyć: funkcje trygonometryczne: podstawowy, w płaszczyźnie kartezjańskim, przykłady, ćwiczenia

2 + 2 + 10 = 6 - 2 + 10

Liczba 10 może zostać anulowana bez utraty równości, pozostawiając kolejną krótszą równość i równoważność poprzedniej:

2 + 2 = 6 - 2

W równości (10 ÷ 2) - 3 = 5 - 3 liczba całkowita - 3 należy do obu członków równości i pojawia się jako dodanie, dlatego można je anulować, uzyskując:

10 ÷ 2 = 5

Dzieje się tak również z dosłownymi ilościami, na przykład:

Tak x + 2y + z = −a + b + z

Następnie „Z” można anulować, ponieważ znajduje się po obu stronach równości jako dodawanie (i z tym samym znakiem).

Czyniąc to, powoduje:

x + 2y = −a + b

Może również zdefiniować właściwość anulowania mnożenia. Jeśli ta sama kwota C pomnoże oba członki równości, ta kwota może zostać anulowana, na przykład:

Cx = Cy

Następnie C można anulować, aby uzyskać po prostu:

x = y

5.- Własność jednorodności

Równość pozostaje niezmienna poprzez dodanie, odejmowanie, mnożenie lub dzielenie przez tę samą ilość po obu stronach tego samego.

Na przykład ma 8 + 5 = 13, jeśli obaj członkowie mnożą się przez pewną dowolną liczbę c = 2, równość pozostaje:

(8+5) × 2 = 13 × 2

13 × 2 = 26

Matematyczne równe klasy

Istnieją różne rodzaje równości matematycznej, więc są one klasyfikowane dla ich najlepszego zrozumienia w:

-Tożsamości, Są równością, w której obaj członkowie są identyczni:

2 = 2
x = x
2x = x + x

i tak dalej.

-Równania, Są to równości, w których pojawiają się jedna lub więcej niewiadomych i jest prawdziwe w przypadku niektórych wartości, to znaczy równość nie jest spełniona dla żadnej dowolnej wartości, więc są one również znane jako znane jako również jako znane jako Warunkowe równości. Przykłady:

x + 1 = 5

X³ = 27

A + B = 40

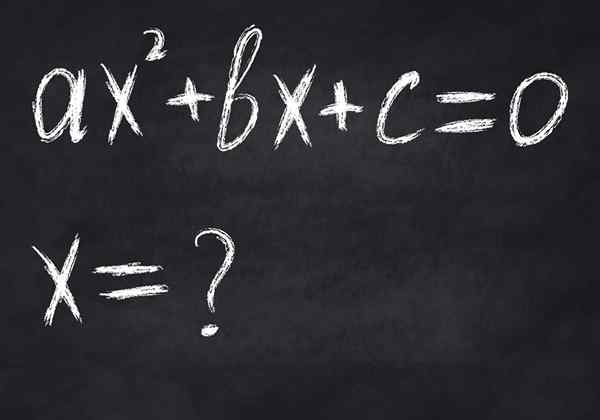Rysunek 2.- Równanie jest warunkową równością matematyczną, ponieważ jest spełnione tylko dla niektórych wartości zmiennych. Obraz pokazuje równanie drugiego stopnia, które najwyżej ma dwa prawdziwe rozwiązania

-Równoważniki, W nich członek lewicy jest równoważny z tym po prawej, nawet jeśli nie są one równe, na przykład w: 2³ = 8.

Może ci służyć: zasada addytywna

-Formuły, Jest to równość, która jest zawsze wypełniona dla wartości zmiennej niezależnej, jak w dobrze znanej wzorze dla odległości D w zależności od czasu T telefonu komórkowego z jednolitym ruchem prostoliniowym: D = v ∙ t

Rozwiązane ćwiczenia

Ćwiczenie 1

Napisz liczbę od 10 do czterech różnych i równoważnych równości.

Rozwiązanie

Wszystkie te równość wyrażają numer 10, ale na różne sposoby:

5 × 2 = 10

11-1 = 10

10¹= 10

20 ÷ 2 = 10

Ćwiczenie 2

Jaka jest wartość x, która spełnia równość x + 1 = 3?

Rozwiązanie

Ta równość jest równaniem, ponieważ wartość x jest nieznana. Za pomocą właściwości 5, jeśli dodano wyrażenie x + 1 = 3 (-1) po obu stronach symbolu „=”, równość pozostaje:

x + 1 + (−1) = 3 + ( - 1)

Podczas dodawania (−1) do członka lewej i operacji jest rozwiązane, „x” jest sam po lewej stronie równości, ta procedura jest wywoływana luz:

x + 1 - 1 = 3–1

x = 2

Dlatego wartość spełniająca tę równość wynosi x = 2.

Ćwiczenie 3

Jeśli telefon z jednolitym ruchem prostoliniowym ma prędkość 2.5 m/s, jaka jest odległość, która działa po 3 sekundach?

Rozwiązanie

Stosowany jest formuła widoczna w poprzedniej sekcji, D = v ∙ t, w którym wymieniono wartość V:

D = 2.5 ∙ t

Wyrażenie staje się równością, gdy t = 3 sekundy, a operacja jest rozwiązana:

D = 2.5 ∙ 3 m = 7.5m

Co powoduje równość:

D = 7.5m

Bibliografia

1. Barnett, r. 2000. Wstępne sculpture. 4. Wydanie. McGraw Hill.
2. Larson, r. 2012. Wstępne sculpture. 8. Wydanie. Cengage Learning.
3. Pérez, v. Właściwości równości algebraicznej. Odzyskane z: matematyki.Laguia2000.com.
4. Właściwości równości. Źródło: PPS.K12.Lub.nas.
5. Stewart, J. 2007. Kalkulacja wstępna: matematyka do obliczeń. 5. Wydanie. Cengage Learning.