ICOSONO

Co to jest icogon?

A ICOSONO lub ISODECAGON Jest to wielokąt, który ma 20 stron. Wielokąt jest płaską postacią utworzoną przez skończoną sekwencję segmentów linii (więcej niż dwa), które obejmują region płaszczyzny.

Każdy segment linii nazywa się bokiem, a przecięcie każdej pary boków nazywa się wierzchołkiem. Zgodnie z liczbą boków wielokąty otrzymują określone nazwy.

Najczęstsze są trójkąt, czworoboczny, pentagon i sześciokąt, które mają odpowiednio 3, 4, 5 i 6.

Charakterystyka iCogon

Poniżej znajdują się cechy wielokątów i ich zastosowania w icogon.

1- Klasyfikacja

Icosgono, będąc wielokątem, można klasyfikować jako regularne i nieregularne, gdzie zwykłe słowo odnosi się do faktu, że wszystkie strony mają taką samą długość i kąty wewnętrzne, które mają tak samo; W przeciwnym razie mówi się, że wyścig (wielokąta) jest nieregularny.

2- ISODECAGON

Regularny icosgon jest również nazywany zwykłym izodogonem, ponieważ aby uzyskać zwykły iCosgon -Gauge to, co należy zrobić, to bisecar (podziel na dwie równe części) z każdej strony zwykłego decagonu (10 stron wielokąta).

3- obwód

Aby obliczyć obwód „P” zwykłego wielokąta, liczba boków jest mnożona przez długość każdej strony.

W konkretnym przypadku iCogon obwód jest równy 20xl, gdzie „L” jest długością każdej strony.

Na przykład, jeśli masz regularny wycios po stronie 3 cm, jego obwód jest równy 20 x 3 cm = 60 cm.

Oczywiste jest, że jeśli izokagon jest nieregularny, nie można zastosować poprzedniej formuły.

W takim przypadku 20 stron musi być dodawane osobno, aby uzyskać obwód, to znaczy obwód „p” jest równy ∑li, z i = 1,2,…, 20.

4- Piagonal

Liczba przekątnych „D” o wielokątach jest równa n (n-3)/2, gdzie n reprezentuje liczbę stron.

W przypadku icogon musi to być d = 20x (17)/2 = 170 przekątnych.

5- suma kątów wewnętrznych

Istnieje formuła, która pomaga obliczyć sumę wewnętrznych kątów zwykłego wielokąta, które można zastosować do zwykłego icosgonu.

Wzór polega na odejmowaniu 2 do liczby boków wielokąta, a następnie pomnożenia tej liczby przez 180º.

Otrzymuje się ten wzór, że możemy podzielić wielokąt po bokach na trójkąty N-2, a przy użyciu faktu, że suma kątów wewnętrznych trójkąta wynosi 180º Wzór jest uzyskiwany.

Na poniższym obrazie zilustrowano formułę dla engona zwykłego (wielokąta 9.

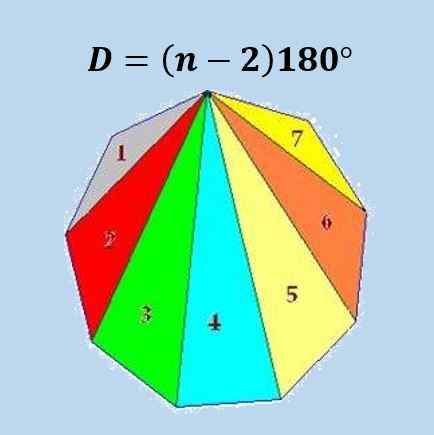
Za pomocą wzoru przedniej, uzyskuje się, że suma wewnętrznych kątów dowolnego wynosi 18 × 180º = 3240º lub 18π.

Obszar 6

Aby obliczyć obszar zwykłego wielokąta, bardzo przydatne jest znanie koncepcji apotemu. ApotheMe to linia prostopadła, która przechodzi od środka zwykłego wielokąta do punktu środkowego dowolnej strony.

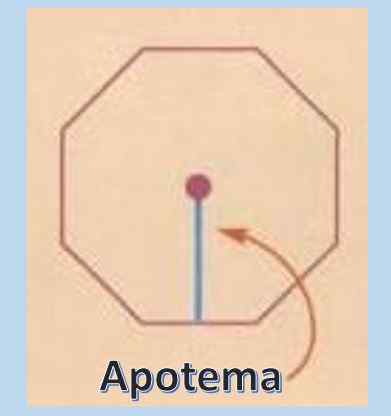
Po znaniu długości apotemu obszar zwykłego wielokąta wynosi a = pxa/2, gdzie „p” reprezentuje obwód i „a” apotem.

W przypadku zwykłego podjazdu masz do swojego obszaru, jest a = 20xlxa/2 = 10xlxa, gdzie „l” jest długością każdej strony i „a” jego apoteme.

Z drugiej strony, jeśli masz nieregularny wielokąt po bokach, aby obliczyć jego obszar, wielokąt jest podzielony na znane trójkąty N-2, wówczas obliczany jest obszar każdego z tych trójkątów N-2 są dodanymi obszarami.

Metoda opisana powyżej jest znana jako triangulacja wielokąta.

Bibliografia

1. Elementy geometrii: z licznymi ćwiczeniami i geometrią kompasu. University of Medellin.
2. Iger. (S.F.). Matematyka pierwszy semestr Tacaná. Iger.