Historia trygonometrii z jej początków

Historia trygonometrii Odnosi się do zestawu faktów i postępów, które miały miejsce wokół tej gałęzi matematyki od jej początków do najnowszych wydarzeń.

Podczas krótkiej podróży przez swoją historię jest oczywiste, że nauka ta urodziła się w odpowiedzi na problemy, przed którymi stoją starożytni astronomowie i nawigatorzy w celu przeanalizowania przemieszczenia gwiazd na niebie.

Termin ten pojawia się po raz pierwszy w książce Trigonometriae Libri Quinque, napisany przez niemieckiego matematyka i naukowca Pitiscusa Bartolomé (1561-1613). Via Wikimedia Commons.

Podobnie słowo trygonometria wynika z składu dwóch greckich słów: Trigonon (trójkąt) i Metron (zakres). Termin ten pojawia się po raz pierwszy w książce Trigonometriae libri quinque, Napisane przez niemieckiego matematyka i naukowca Pitiscusa Bartolomé (1561-1613).

W ten sposób etymologia tego słowa pokazuje, że trygonometria jest badaniem związków między kątami trójkąta a segmentami lub liniami, które go tworzą.

[TOC]

Początki trygonometrii

Pierwsze kroki trygonometrii zostały wykonane przez człowieka, gdy jest promowana przez potrzebę poznania i analizy ruchu gwiazd.

Oznacza to, że opracowany przez człowieka trygonometrię, ponieważ znaleziono w sytuacjach, w których niemożliwe było bezpośrednio dokonywać pomiarów, ponieważ aby obliczyć gwiazdy, wymagane były bardziej złożone narzędzia matematyczne.

- Studia w Babilonie

Tabela błotna napisana przez Babilończyków o nazwie Plimpton 322. Via: Wikimedia Commons

Badania pokazują, że ponad 3 temu.000 lat Babilończycy już poradzili sobie z koncepcją kątów i powodów trygonometrycznych, to znaczy byli w stanie ustanowić relacje między bokami i kątami trójkątów.

Na przykład stół błotny - napisany przez Babilończyków - o nazwie Plimpton 322 (1800 a. C.) pokazuje kolejność kolumn i wierszy zawierających liczby w pisaniu klinowym. Według badań przeprowadzonych przez niektórych ekspertów, tablet ten reprezentuje serię funkcji trygonometrycznych.

Może ci służyć: jakie są wytyczne? (Geometria)

Babilończycy znali koncepcje, które dały powstanie twierdzenia Pitagorasa (569-474 A.C) i rozumieli swoją zasadę.

W ten sam sposób znali również twierdzenie przypisane Thales of Miletus (695-546.C), co wskazuje, że każda prosta, narysowana równolegle do boku trójkąta, tworzy się z pozostałymi dwoma stronami kolejnego trójkąta, który jest podobny do początkowego trójkąta.

- Starożytni Egipcjanie

Starożytnym Egipcjanom udało się utrzymać stok jednolicie na każdej z piramid. Via: Pixabay

Chociaż nie należy mówić o trygonometrii w ogólnej sferze egipskiej matematyki, nie ma wątpliwości, że ta cywilizacja zajmowała się niektórymi koncepcjami trygonometrycznymi.

Dzieje się tak, ponieważ rozważając wielkie budynki wykonane przez Egipcjan, takie jak piramidy, można stwierdzić, że mieli wiedzę na temat trygonometrii.

Podstawowa trudność inżynierska, z jakimi borykają się Egipcjanie - i to rozwiązało niesamowite.

W tym celu zastosowali koncepcję, którą nazywali „seqt”, co jest to równoważne z tym, co dziś rozumiemy jako nachylenie nachylonej płaskiej powierzchni.

Ponadto Egipcjanie dokonali pomiarów na pionowych powierzchniach używanych jako jednostka „łokcie” i w poziomie „ręka”, która odpowiadała 1/7 łokcia. W ten sposób obliczyli SEQT lub w toku w różnych budynkach. Na przykład w piramidzie jufú (Queope) SEQT ma 5 1/2 rąk na łokieć.

- Starożytna Grecja i tabela strunowa

Cała wiedza Babilończyków i starożytnych Egipcjan przeszła do Grecji, gdzie podkreślono matematyk i astronom Nicei (190-120 (190-120. C), który jest uważany za ojca trygonometrii. Hiparco stworzył tabele „Strings”, z którymi udało się rozwiązać problemy płaskich trójkątów.

Nicea Hiparco - Źródło: przeniesione z.Wikipedia do Commons autorstwa Maksima - w ramach domeny publicznej

Aby je wykonać, zastosował obwód o określonym promieniu (promień jest odległością między środkiem koła i dowolnym punktem obwodu).

Może ci służyć: prawdopodobieństwo warunkowe: wzór i równania, właściwości, przykłady

Następnie wypierało promień, aby zdefiniować różne kąty; Podczas tego działania wskazywało w tabeli długość linii, która była wyznaczona po bokach kąta i obwodu.

Te „struny” okazały się prekursorami tabel funkcji trygonometrycznych, których używamy dzisiaj.

- Wkład w Indiach

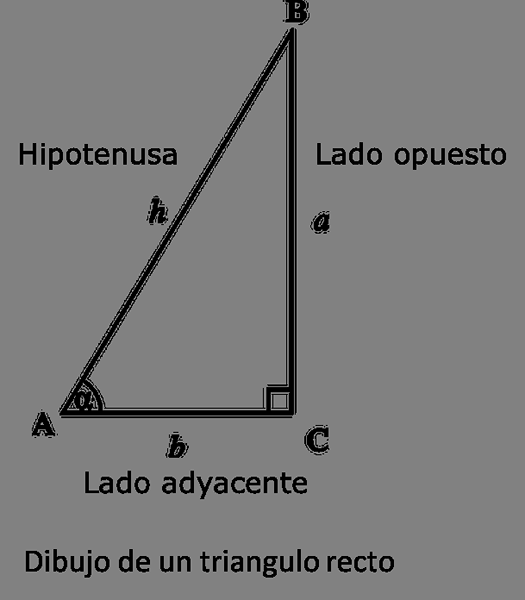Rysunek prawego trójkąta.

Podobnie jak Grecja Uczeni, astronomowie Indii opracowali również system trygonometryczny, ale w przeciwieństwie do Greków, ci astronomowie oparli swoją analizę na funkcji „sinus” zamiast używania strun.

Jednak funkcja „sinus” wyrażona przez tych astronomów nie jest dziś używana; Ta funkcja nie była proporcją (jak dziś używana), ale długość przeciwnej strony do kąta trójkąta prostokąta, którego znana jest hipotencja.

- Arabia i funkcje trygonometryczne

Pod koniec ósmego wieku arabscy ​​astronomowie, pod wpływem badań trygonometrii przeprowadzonych przez narody Grecji i Indii, rozpoczęli ważne badania dotyczące relacji między kątami a ich stronami.

W ten sposób, pod koniec XII wieku, podnieśli dobrze znane funkcje piersi, cosinusa, stycznej, cotangent, suszenia i kombajnu.

Odkryli także i zweryfikowały pierwotne twierdzenia trygonometrii, które są używane w analizie płaskich i sferycznych trójkątów. Ponadto arabscy ​​matematycy zasugerowali użycie jednej wartości („1”) dla radia (r = 1), co dało powstanie nowoczesnych wartości funkcji trygonometrycznych.

- Wkład z Zachodu

Johann Müller znany jako Regiomontanus (1436-1476). Osiągnięta systematyzacja i uogólnienie metod trygonometrycznych stosowanych w obszarze geometrii. Via: Wikimedia Commons

Matematyka Zachodu, szczególnie między dwunastym a piętnastym wiekiem, silnie wpłynęły postulaty starożytnej Grecji, Indii i Arabów.

Może ci służyć: chi-kwadrat (χ²): rozkład, jak jest obliczany, przykłady

W tym czasie decydują się na obszar trygonometrii-wkład Johanna Müllera, znany również jako Regiomontanus (1436-1476). Ten matematyk osiągnął systematyzację i uogólnienie metod trygonometrycznych stosowanych w obszarze geometrii.

Regiomontanus opracował i opublikował traktat, który zadzwonił Triangulis omnimodis libri quinque, który składał się z pięciu książek i w sumie 131 stron.

W tej książce regulował wszystkie koncepcje płaskiej i sferycznej trygonometrii, które następnie były używane przez ważnych astronomów, takich jak: Nicolás Kopernik.

- Trygonometria XVII i XVIII wieku

W XVII wieku badania obliczeń trygonometrycznych prosperowały dzięki wkładowi matematyków, takich jak szkocka John Napier (1550-1617), którzy podniosły różne metody rozwiązywania sferycznych trójkątów.

John Napier. Źródło: przez Encard autorstwa Samuela Freemana (1773–1857) [domena publiczna], przez Wikimedia Common

Później, w XVIII wieku, wkład szwajcarskiego matematyka Leonharda Eulera (1707-1783) był decydujący, ponieważ jego badania położyły podstawy nowoczesnej trygonometrii, wprowadzając notację, która jest obecnie używana do funkcji trygonometrycznych.

Ponadto Euler udało się zdefiniować funkcję wykładniczą i odkrył swój związek z funkcjami trygonometrycznymi, co pozwoliło mu opisać cechy trygonometrii.

Następnie Sir Isaac Newton (1643-1727), poprzez wynalezienie rachunku różnicowego i integralnego, ułatwił reprezentację dużej liczby funkcji matematycznych, w tym trygonometryczne. W ten sposób trygonometria stała się częścią analizy matematycznej, w której dziś odgrywa podstawową rolę.

Ilustracja Sir Isaac Newton

Bibliografia

1. Mansfield, Daniel. Wildberger, n. (2017). Plimpton 322 to Babilońska dokładna trygonometria seksualna. Pobrano 20 maja 2020 r. Z: Scientedirect.com
2. Jimenez s. (2017). Historia trygonometrii i jej zastosowań. Pobrano 23 maja 2020 r. Deedu
3. Pérez, v. (2010). Historia trygonometrii. Pobrano 22 maja 2020 r. Z: Laguia2000.com
4. S.DO. (S.F.) Trygonometria. Pobrano 23 maja 2020 r. Z: Blogspot.com
5. Merlet, Jean-Pierre (2004). Uwaga na temat historii funkcji trygonometrycznych. Pobrano 22 maja 2020 z: netto
6. Adamek, t., Penkalski, k., Valentine, g. (2005). Historia trygonometrii. Pobrano 23 maja 2020 r. Z: Citseseerx.Ist.PSU.Edu/