Matematyka

Geometria euklidyjska

Geometria euklidyjska

Wyjaśniamy, jaka jest geometria euklidyjska, jej historia, elementy i podajemy kilka przykładów

Euclid z Aleksandrii i jej elementów, autorstwa Jusepe de Ribera, obok, dwie nierównoległe linie i linia, która je przecina, ilustrując piąty postulat. Źródło: Wikimedia Commons.

Co to jest geometria euklidyjska?

Geometria euklidyjska Jest to ten, który rządzą postulatami przez Euclida de Alejandría, greckiego geometru, który żył w kierunku 300.C, na którego cześć nazywana jest ta dyscyplina, ponieważ jako pierwsza ją usystematyzowała.

Ta gałąź matematyki bada właściwości linii, samolotów, kątów i postaci geometrycznych, takich jak wielokąty, obwody i inne stożki. Stąd jego znaczenie w nauce i inżynierii, których rozwój znacznie skłonił.

Z drugiej strony geometria euklidesowa była pierwszą nauką ścisłą, ponieważ wraz z nią rozpoczęła się ścieżka systematyzacji nauki, a także użycie logiki do wykazania, z kilku aksjomatów, licznych propozycji zwanych twierdzeniami, w celu opisania właściwości obiektów geometrycznych.

Historia

Geometria ma długą historię, ponieważ zainteresowanie ludzkości jest bardzo stare, a ośrodkowa oś geometrii euklidesowej jest dziełem Rzeczy, mądrego euclida w Aleksandrii, miasta położonym w Egipcie i który żył w czwartym wieku.C.

W tym czasie znane były najważniejsze właściwości wielu liczb i ciał geometrycznych. Była obszerna wiedza na temat geometrii, ale wszystko było empiryczne i brakowało systematyzacji.

Następnie król Egiptu Ptolemeusz i powierzył już znanego nauczyciela Euclida, którego szkoła była w Aleksandrii, aby zorganizować całą dostępną wiedzę matematyczną i geometryczną, w tym twierdzenia i nieruchomości.

Euclides zaczął pracować, a obok swoich uczniów napisał swoje elementy pracy, które podzielił na trzynaście książek, jako rozdziały. Ta praca stałaby się odniesieniem do geometrii dla przyszłych pokoleń.

Może ci służyć: kolejne pochodne

Elementy Euclida

Treść elementów jest zorganizowana w następujący sposób:

  • W książkach I do IV rozwija się płaska geometria.
  • W książkach V i widzieliśmy teorię proporcji.
  • Książki IX są poświęcone arytmetyce.
  • W książce x pojawia się w książce x,
  • Geometria przestrzeni w książkach XI do XIII.

Geometria euklidesowa była podstawą wielu tylnych rozwoju geometrycznego i obecnie jest uczy się we wszystkich szkołach na świecie.

Ma również zalety bycia pierwszą pracą obejmującą staranne demonstracje oparte na logicznym rozumowaniu, a także w zakresie spójności wobec ciała geometrycznej i matematycznej w tamtych czasach.

Podstawowe elementy geometrii euklidesowej

Geometria euklidesowa jest zbudowana wokół czterech podstawowych elementów, opisanych w Księdze I elementów:

  1. Miejsce
  2. Prosty
  3. Płaski
  4. Przestrzeń

1. Miejsce

A miejsce Brakuje wymiarów lub części i odróżnia się od innego punktu po prostu swoim lokalizacją. Jeśli dwa punkty A i B są różne, to dlatego, że mają różne pozycje, które są wskazane przez dobrze znane współrzędne kartezjańskie (x, y), jeśli punkt jest w płaszczyźnie lub współrzędnych (x, y, z) Jeśli jest w kosmosie.

Warto zauważyć, że system kartezjański nie jest częścią Rzeczy euclida, ale pojawił się znacznie później w ciągu 1600 lat i jest spowodowany René Descartes.

2. Prosty

prosty Jest to nieskończona zbiór punktów i ma tylko długość, a nie szerokość. Część jest zwykle rysowana, a strzałki w obu wskazuje, że linia trwa w nieskończoność.

3. Płaski

A płaski Jest nieograniczoną powierzchnią, więc ma dwa wymiary i których część jest reprezentowana, za pomocą kwadratu lub prostokąta.

Tam, w płaszczyźnie, istnieje wiele postaci geometrycznych, takich jak linie, otwarte i zamknięte krzywe i wielokąty,.

Może ci służyć: ogólne równanie linii, której nachylenie jest równe 2/3

4. Przestrzeń

Wreszcie jest przestrzeń Z trzema wymiarami, zdolnymi do obarwania wszystkich punktów. Zawiera płaszczyzny i ciała geometryczne charakteryzujące się ich objętością, takimi jak wielościan, kule i inne.

Można je uznać za podstawowe definicje geometrii euklidesowej, ale oprócz nich Euklides oferuje około 150 różnorodnych definicji w ich pracy.

Powszechne pojęcia

Składają się one z oczywistych i intuicyjnych faktów, które nie należą odpowiednio do zakresu geometrii i są wykorzystywane w miarę rozwoju koncepcji. Odnoszą się do „rzeczy” w bardzo szerokim kontekście:

  1. Rzeczy takie same z czymś innym, są takie same ze sobą.
  2. Jeśli sprawy są dodawane do innego zestawu rzeczy, a wszystkie są takie same, jakie wyniki są takie same.
  3. Jeśli równe rzeczy zostaną skradzione, pozostałe.
  4. Kiedy wszystko się ze sobą pokrywają, dzieje się tak, ponieważ są takie same.
  5. Cała jest zawsze większa niż strony, przyjmowane osobno.

Postulaty geometrii euklidesowej

Postulaty lub aksjomaty są prostymi stwierdzeniami, które są uważane za prawdziwe i oczywiste, więc nie wymagają demonstracji.

Stanowią one podstawę geometrii euklidów i euklidów ustanawia pięć w swojej książce I:

  1. Być dwoma różnymi punktami do i b, przechodzi tylko jedna linia, to znaczy dwa punkty określają linię.
  2. Każdy segment prostoliniowy można rozszerzyć w nieskończoność, aby stanowić linię, dlatego każdy segment należy do linii.
  3. Jeśli masz dwa różne punkty lub a, zawsze możesz narysować okrąg ze środkiem w O i promieniu równym segmentowi OA.
  4. Wszystkie proste kąty są ze sobą przystające.
  5. Biorąc pod uwagę linię i punkt P, który do niej nie należy, zawsze jest to możliwe.

Ostatni postulat, szczególnie w swojej oryginalnej wersji, nie wygląda tak prosto, jak inne. Twierdzi, że:

Może ci służyć: heptagon

„Jeśli linia prosta, która spadnie na dwóch innych liniach, produkuje dwa kąty wewnętrzne po tej samej stronie mniej niż dwa proste kąty, powiedziane linie proste, powszechne w nieskończoność, są (przecinające się) z boku, po których drobne kąty są takie dwa proste kąty ”.

To znaczy pierwotnie postulat 5 ustanawia ten warunek, aby dwie linie nie były równoległe. Ale jest to wyraźniejsze, gdy jest napisane w taki sposób, że ilustruje odwrotnie, to znaczy równoległość linii.

Przykłady geometrii euklidesowej

Przykład 1

Istnieją trzy różne punkty, oznaczone literami A, B i C.

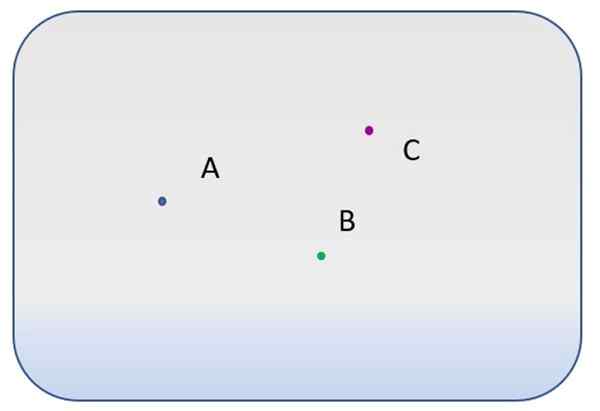
  1. Ile różnych linii przechodzi przez punkt A?
  2. I ile można narysować między punktami A i B? I między A i C?
  3. Czy można narysować linię, do której punkty A, B i C?

Odpowiedz

Według Postulatu I, nieskończone linie proste można rysować przez A, ponieważ wymagane są dwa punkty do ustalenia linii.

Odpowiedź b

Entre A i B można narysować tylko linię. I między A i C.

Odpowiedź c

Nie jest możliwe jednocześnie zawieranie linii, B i C.

Przykład 2

Poproszono o zbudowanie krok po kroku trójkąt równoboczny (wszystkie jego boki są równe), znając jedną z jego stron, która jest segmentem AB i wskazując na każdym etapie postulat lub powszechne pojęcie zastosowane w budownictwie w konstrukcji w konstrukcji w.

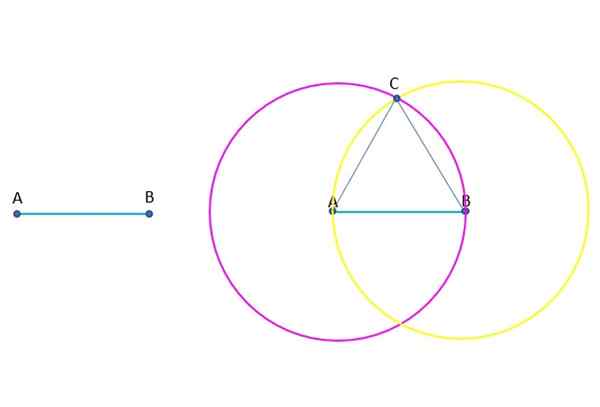Budowa trójkąta równobocznego ABC. Źródło: f. Zapata.

Odpowiedź

Krok 1

Narysowany jest okrąg z centrum A i Radio AB. Jest to zawsze możliwe, według Postulatu III.

Krok 2

Narysowany jest kolejny obwód z środkiem w B i Radio AB, a postulat III jest ponownie stosowany.

Krok 3

Oba obwody, które mają ten sam promień, są cięte w punkcie C. Teraz możesz rysować segmenty, które jednoczą C z odpowiednio A i B, zgodnie z Postulatem I.

Segmenty te są radiom o obwodzie, a zatem miary AC i BC są równe miarom AB, zgodnie ze wspólnym pojęciem 1. Następnie trójkąt ABC jest równoboczny.