Podstawowe funkcje trygonometryczne, w płaszczyźnie kartezjańskiej, przykłady, ćwiczenia

funkcje trygonometryczne Zmiennej rzeczywistych odpowiadają dowolnym kątowi (wyrażonym w radianach), trygonometrycznym rozumowi, który może być sinusoidalny, cosinus, styczna, cotangent, sekunda i harowanie.

W ten sposób mamy sześć funkcji trygonometrycznych: zatok, cosinus, styczna, kombajn, suszenie i cotangent.

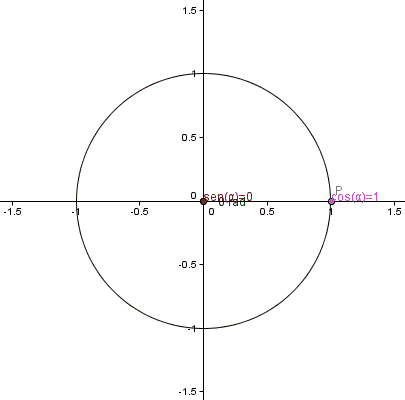Rysunek 1. Animacja kręgu trygonometrycznego. Źródło: Wikimedia Commons.

Funkcje trygonometryczne dla kątów między 0 a 2π są zdefiniowane za pomocą jednolitego obwodu, radia 1 i którego centrum pokrywa się z pochodzeniem układu współrzędnych kartezjańskich: punkt (0,0).

Możemy zlokalizować dowolny punkt P współrzędnych (x, y) na tym obwodzie.

Segment, który łączy pochodzenie z P, wraz z odpowiednimi segmentami łączącymi projekcje P na osiach współrzędnych, tworzą trójkąt prostokąta, którego przyczyny trygonometryczne są znane jako iloraz między bokami trójkąta. Więc:

• sin θ = przeciwny /hipotenusa cateto
• cos θ = sąsiadujący /hipotenusa cateto
• tg θ = przeciwne cateto /sąsiednie cateto

A teraz powody, które są odwrotnością powyższych:

• sec θ = hipotenusa /sąsiadujący Cateto
• Szkoda θ = hipotenusa /cateto przeciwieństwo
• CTG θ = sąsiadujący Cateto /przeciwny Cateto

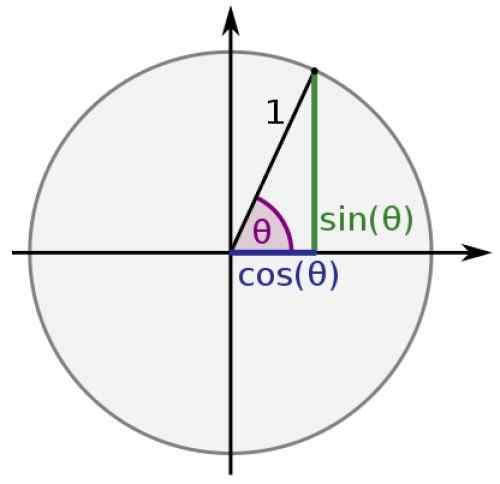
W jednolitym kręgu hipotencja dowolnego trójkąta jest równa 1, a kategorie są warte x i y, zatem:

sin θ = y

cos θ = x

Rysunek 2. Prawy trójkąt w okręgu jednostkowym. Źródło: Wikimedia Commons.

W ten sposób funkcje sinusoidalne i cosinus zawsze nabierają wartości między -1 do 1, podczas gdy pozostałe:

tg θ = y/x

szkoda θ = 1/y

Sec θ = 1/x

Nie są zdefiniowane, kiedy X albo I Są warte 0.

[TOC]

Funkcje trygonometryczne w płaszczyźnie kartezjańskiej

Jak zobaczymy poniżej, funkcje trygonometryczne charakteryzują się okresem. Dlatego nie są biustonose, z wyjątkiem ograniczonej domeny.

Funkcja f (x) = sin x

Zaczynając w kręgu trygonometrycznym w punkcie P (1.0), kąt wynosi 0 radianów. Następnie promień obraca się w sensie antyhorarycznym, a funkcja Sen X rośnie stopniowo, aż osiągnie radiany π/2 (90º), co odpowiada 1.Około 571 radian.

Może ci służyć: kąty uzupełniające: co to są, obliczenia, przykłady, ćwiczenia

Tam osiąga wartość y = 1, a następnie maleje, aż osiągnie zero w π radian (180 °). Następnie zmniejsza się jeszcze bardziej, ponieważ wartość staje się ujemna do osiągnięcia −1, gdy kąt wynosi 3π/2 radian (270 °).

Wreszcie, wzrasta ponownie, aż powróci do zera w 360 °, gdzie wszystko zaczyna się od nowa. To sprawia, że ​​y = sin x a funkcja okresowa z okresu 2π, więc funkcja zatok nie jest biornica.

Ponadto wykres jest symetryczny w odniesieniu do punktu (0,0), dlatego funkcja jest dziwna.

Następnie wykres y = Sen x:

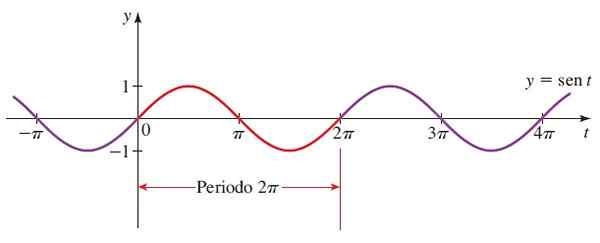Rysunek 3. Wykres funkcji f (x) = sin x. Źródło: Stewart, J. Prefrecculment: Mathematics for the University.

Czerwona sekcja to pierwszy okres. Rozważane są również kąty ujemne, ponieważ promień koła trygonometrycznego może obracać się w harmonogramie.

Domena Sen X = Wszystkie prawdziwe.

Sen x Range lub trasa = [-1,1]

Funkcja f (x) = cos x

W punkcie P (1.0) Funkcja Coseno jest warta 1 i stamtąd maleje, osiągając 0, gdy kąt wynosi π/2. Kontynuuj zmniejszanie się i przyjmuje wartości ujemne, aż osiągnie -1 pod kątem π.

Następnie zaczyna rosnąć stopniowo, aż osiągnie 0 w 3π/2 i ponowne przyjmuje wartość, gdy promień obróci pełny obrót. Stamtąd cykl jest powtarzany, ponieważ cos x jest okresowy i jest również moment obrotowy (symetryczny wokół osi pionowej).

Forma funkcji cosinus jest taka sama jak forma zatoki, chyba że są one przesunięte π/2 w odniesieniu do drugiej.

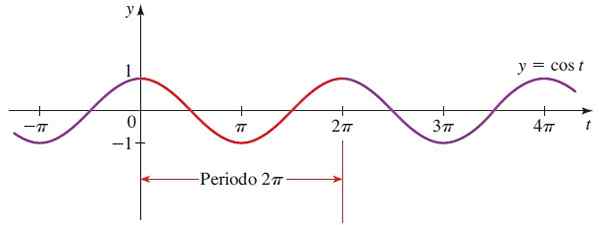Rysunek 4. Wykres funkcji f (x) = sin x. Źródło: Stewart, J. Prefrecculment: Mathematics for the University.

Domena cos x = Wszystkie prawdziwe.

Może ci służyć: punktualne oszacowanie

Zakres lub trasa cos x = [-1,1]

Nieciągłe funkcje trygonometryczne

Funkcje tg x, ctg x, sec x i hars. Ponieważ są one warte 0 pod niektórymi kątami, kiedy pojawiają się w mianowniku, sprawiają, że funkcja nie była.

A ponieważ zatok i cosinus są funkcjami okresowymi, funkcje tg x, ctg x, sec x, szkodę x są również.

Funkcja styczna f (x) = tg x

Dla funkcji stycznej wartości nieciągłości wynoszą: ± π/2, ± 3π/2, ± 5π/2 ... Funkcja ma bardzo duże lub bardzo małe wartości. Zasadniczo zdarza się to dla wszystkich wielokrotności π formy (2n+1) π/2, zarówno dodatnie, jak i ujemne, z n = 0, 1, 2 ..

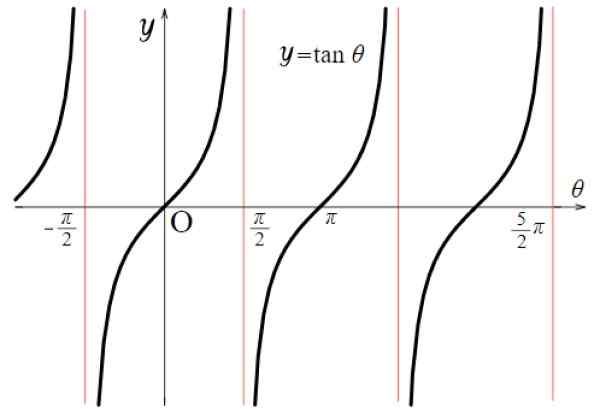Rysunek 5. Wykres funkcji f (x) = tg x. Źródło: Wikimedia Commons.

Dlatego:

Domena TG x: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Ranga lub TG X Tour: Wszystkie prawdziwe.

Zauważ, że funkcja f (x) = tg x jest powtarzana między - π/2 i + π/2, dlatego jej okres wynosi π. Ponadto jest symetryczny w odniesieniu do pochodzenia.

Funkcja Cotangent f (x) = ctg x

Dla tej funkcji wartości nieciągłości występują w 0, ± π, ± 2π…, to znaczy całe wielokrotności π π.

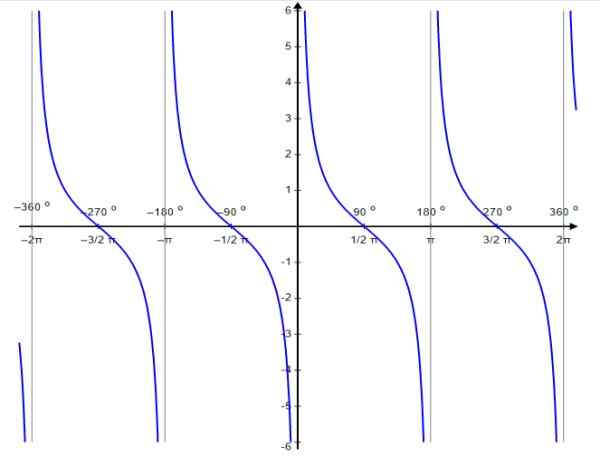Rysunek 6. Wykres funkcji F (x) = COTG x. Źródło: Wikimedia Commons.

Podobnie jak funkcja styczna, funkcja Cotangent jest okres okresowy π. Dla niej jest spełnione:

Domena CTG x: D = x ∈ R / x ≠ n π; n ∈ Z

CTG X lub trasa: Wszystkie prawdziwe.

Funkcja suszenia f (x) = sec x

Funkcja Sec X ma punkty nieciągłości w ± π/2, ± 3π/2, ± 5π/2… gdzie cos x = 0. Jest to również okres okresowy π i obserwuje się również wykres, że funkcja nigdy nie przyjmuje wartości w przedziale (-1,1)

Może ci służyć: liczby całkowitym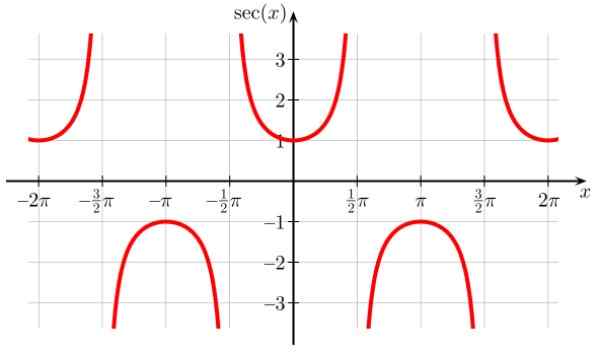 Rysunek 7. Wykres funkcji f (x) = sec x. Źródło: Wikimedia Commons.

Doma of Sec x: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Sec X zakres lub trasa: Wszystkie reais z wyjątkiem (-1,1)

Funkcja zbioru f (x) = szkoda x

Jest podobny do funkcji suszenia, chociaż jest przesunięte w prawo, dlatego punkty nieciągłości wynoszą 0, ± π, ± 2π i wszystkie całe mnożniki π. Jest to również okresowe.

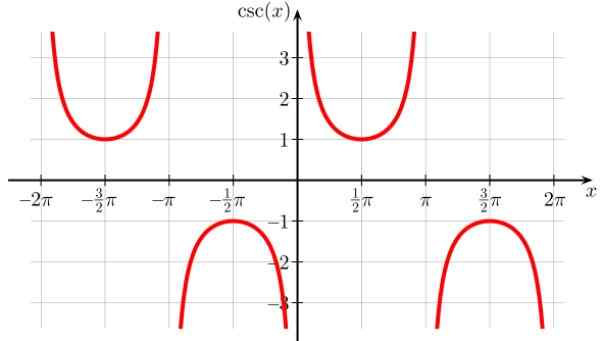Cyfra 8. Wykres funkcji f (x) = szkoda x. Źródło: Wikimedia Commons. Geek3/cc by-SA (https: // creativeCommons.Org/licencje/nabrzeże/4.0)

Domena Harm X: D = x ∈ R / x ≠ n π; n ∈ Z

Zakres lub trasa harmonii: Wszystkie reais z wyjątkiem (-1,1)

Ćwiczenie rozwiązane

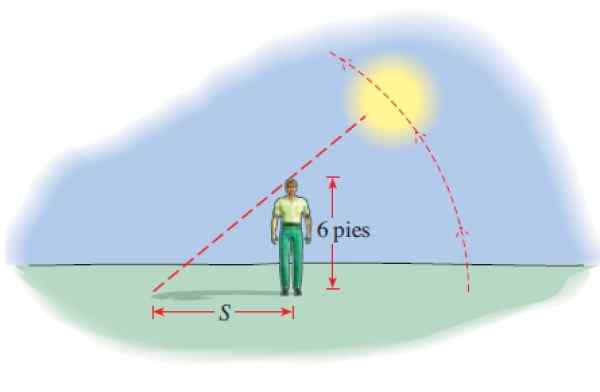
6 -stóp wysoki mężczyzna projektuje cień, którego długość jest podana przez:

S (t) = 6 │Cot (π.T/12) │

Z S u stóp i liczba godzin po 6 rano. Ile wynosi cień o 8 rano, o godzinie 12 m, o godz?

Rozwiązanie

Musimy ocenić funkcję dla każdej z podanych wartości, należy zauważyć, że wartość bezwzględna musi podjąć, ponieważ długość cienia jest dodatnia:

-O 8 rano upłynęły 2 godziny od 6 rano, dlatego t = 2 i s (t) to:

S (2) = 6 │Cot (π.2/12) │Pies = 6 │COT (π/6) │Pies = 10.39 stóp.

-Kiedy ma 12 N, t = 6 godzin upłynęło, zatem:

S (6) = 6 │Cot (π.6/12) │Pies = 6 │Cot (π/2) │Pies = 0 stóp. (W tym czasie słońce spada pionowo na głowie osoby).

-O 14.00 spędzili t = 8 godzin:

S (8) = 6 │Cot (π.8/12) │Pies = 6 │Cot (2π /3) │Pies = 3.46 stóp.

-Kiedy jest 17:45, 11 minęło 11.75 godzin od 6 rano:

S (11.75) = 6 │Cot (π x 11.75/12) │pies = 91.54 stóp. W tej chwili cienie stają się dłuższe.

Czy czytelnik może obliczyć czas, w którym cień osoby jest równa jej wysokości?

Bibliografia

1. Carena, m. 2019. Podręcznik matematyki przednicznicy. National University of the Coast.
2. Figuera, J. 1999. Matematyka. 1st. Urozmaicony. Bolivarian Collegiate Editions.
3. Hoffman, J. Wybór problemów z matematyką. Tom 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.