Funkcje matematyczne

Funkcja matematyczna to związek między dwoma wielkościami, gdy pierwszy zależy od drugiego. Shuttersock

Jakie są funkcje matematyczne?

Funkcje matematyczne Są wyrażeniem w języku matematycznym relacji między dwiema zmiennymi, a wartość pierwszej zmiennych zależy od drugiego. Zwykle zmienne te są symbolizowane z literami X i Y.  Zmienna X nazywana jest domeną lub zmienną niezależną; oraz do Y, Codominium lub zmiennej zależnej.

Spójrzmy na przykład. Mamy dwie zmienne lub wielkości: dolar i centy. Wiemy, że 100 centów jest równoważne do dolara. Dlatego centy (x) to domena, a dolar (y) odpowiada kodominium. Związek ten można wyrazić za pomocą następującej funkcji (f):

F (x) = y / 100

Jeśli mam 143 centów w moim banku Piggy i chcę wiedzieć, ile zaoszczędziłem, stosuję tylko tę funkcję:

F (x) = 143 /100

Dlatego mam 1,43 USD.

Możemy również wyrazić odwrotną relację, to znaczy, że dolar jest równoważny 100 centów. W konsekwencji inwestowane są kategorie zmiennych: dolar (x) staje się domeną, podczas gdy centy jest kodominium. Wyrażamy to w ten sposób:

F (x) = x x 100

Jeśli mam 1,43 $ w moim banku Piggy, ale chcę wiedzieć, ile centów ta liczba jest równoważna, wystarczy zastosować tę drugą funkcję.

F (x): 1,43 x 100

Wynik powraca do moich 143 oryginalnych centów.

Zmienne funkcji matematycznych

Zmienna to po prostu symbol (x, y, z), który reprezentuje różnorodne elementy.

W poprzednim przykładzie zmienne x i y symbolizowały dolara i grosza dolara. Ale te same symbole (x i y) mogą być używane do reprezentowania nieskończoności pierwiastków, takich jak: wiek osoby i ich waga; liczba lotów do określonego miejsca docelowego i okres (tygodniowo, miesięcznie, rocznie) itp.

Może ci służyć: podział syntetyczny

Zmienne można podzielić na wiele typów, ale najważniejsze dla funkcji matematycznych są następujące:

• Zmienna zależna: ci, których wartość zależy od wartości przypisanej do innych zmiennych w ramach funkcji.
• Zmienna niezależna: Zmiany tego rodzaju zmiennej wpływają na wartości reszty zmiennych funkcji.
• Zmienna ilościowa: Jest wyrażany przez określone kwoty numeryczne. Mogą to być liczby całościowe lub dziesiętne.

Charakterystyka funkcji matematycznych

1- Związek między zmiennymi wyraża się w kategoriach równoważności.

2- Dla każdej wartości zmiennej x jest a tylko równoważny zmiennej i. I odwrotnie: dla pewnej wartości y jest i tylko wynik zmiennej x.

3- Mogą być reprezentowane graficznie na płaszczyźnie kartezjańskiej, co pozwala przewidzieć zachowanie jednej z zmiennych z drugiej.

4- Współczesna definicja funkcji matematycznej wynika z niemieckiego matematyka Petera Dirichleta (1805–1859), który opublikował ją w 1837 roku.

Rodzaje funkcji matematycznych

Funkcje matematyczne można klasyfikować zgodnie z różnymi kryteriami, takimi jak związek ustalony między zmiennymi x i y o zachowanie matematyczne funkcji.

Wśród głównych typów są następujące:

Funkcje algebraiczne

Charakteryzują się ustanowieniem związku między składnikami wyrażanymi przez monomianów lub wielomian. Związek ten można określić za pomocą prostych operacji matematycznych, takich jak odejmowanie, mnożenie, podział, suma, wzmocnienie lub nadawanie.

Funkcje liniowe

Gdy są reprezentowane na płaszczyźnie kartezjańskiej, pojawiają się w kształcie linii prostej, która przecina oś współrzędnej w określonym punkcie. Stąd ich nazwa, chociaż są również znane jako funkcje pierwszego stopnia.

Może ci służyć: wspólny czynnik: cechy, przykłady, ćwiczenia

Funkcje na kawałki

W tym typu wartość Codominium i zmienia zachowanie funkcji. Istnieją zatem dwa interwały o różnych zachowaniach w odniesieniu do wartości domeny.

Funkcje transcendentne

Są to bardzo złożone funkcje. Wspólne operacje algebraiczne nie są wystarczające (odejmowanie, mnożenie, podział, suma, wzmocnienie lub promieniowanie) w celu ustalenia związku między zmiennymi, więc należy użyć innych narzędzi matematycznych, takich jak pochodne, całki lub logarytm.

Funkcje trygonometryczne

Ten typ funkcji pokazuje związek liczbowy, który istnieje między różnymi elementami trójkąta i innymi postaciami geometrycznymi, szczególnie wśród jego kąta. Formuły dla piersi, cosinus, styczna, sekunda i harmonte są przykładami tego rodzaju funkcji.

Funkcje iniekcyjne

Funkcje tego typu charakteryzują się specyfiką związku między domeną a kodominium. Do każdej z wartości tych ostatnich tylko jednej wartości domeny odpowiada. Może się również zdarzyć, że wartość domeny nie ma żadnej odpowiedniej wartości w kodominium.

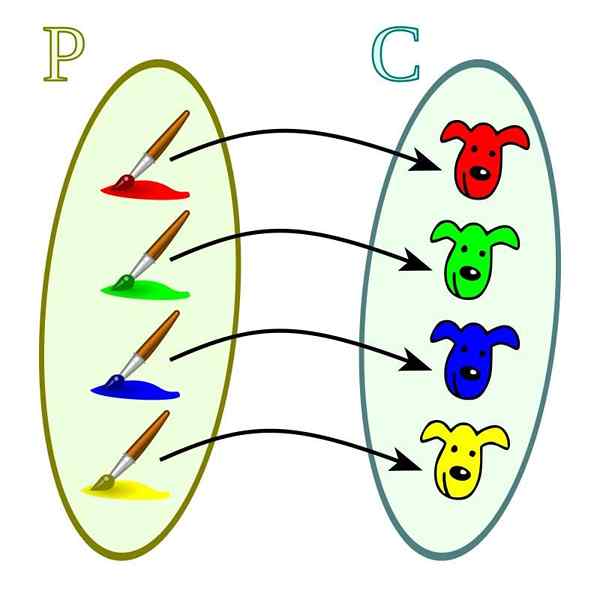Funkcja iniekcyjna. Źródło: Wikimedia Commons

Funkcje onjective

W takim przypadku każda z wielkości kodominium jest związana z co najmniej jedną z wartości domeny. Odróżniają się od funkcji iniekcyjnych, w których wartości Codominium mogą być powiązane z więcej niż jedną z wartości domeny.

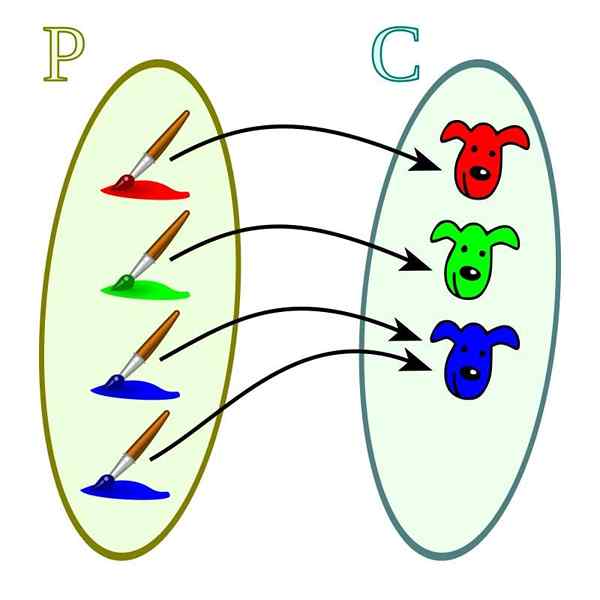Funkcja zatrzymująca. Źródło: Wikimedia Commons

Funkcje biejcive

Ten typ funkcji przedstawia właściwości zarówno iniekcyjne, jak i zatwierdzające.

Do czego są funkcje matematyczne?

Funkcje są szeroko stosowane we wszystkich naukach, które mają matematykę jako naukę pomocniczą. Tak jest w przypadku fizyki, inżynierii, medycyny, finansów, statystyki, między innymi.

Może ci służyć: Rozkład częstotliwości: jak zrobić tabelę, przykład, ćwiczenie

W codziennym życiu

Możemy jednak być również przydatne do rozwiązywania prostszych problemów z codziennymi.

Wyobraź sobie, że twój dziadek dał ci 10 monet, które wydasz na czekoladę. W kiosku podałeś 10 monet na utrzymanie, mówiąc mu, aby dał ci wszystkie czekoladki, które można kupić za pomocą takiej walut. Dali ci 5 czekoladek. Jaka jest cena każdego?

Proponujemy problem: jeśli 5 czekoladek jest równa 10 monet, to ile monet jest równoważne jednej czekoladzie?

Nasza niezależna zmienna (x) to ilość czekoladek (5), podczas gdy zmienna zależna (y) odpowiada liczbie walut, to znaczy 10.

Wyrażamy funkcję w następujący sposób:

F (x) = 2x/x

F (x) = 2 (5)/5

F (x) = 10/5

F (x) = 2

I mamy już odpowiedź: każda czekolada kosztuje 2 monety.

Bibliografia

1. (s/f). Funkcje podstawowe. Witryna funkcji matematycznych. Zaczerpnięte z funkcji.Wolfram.com.
2. (s/f). Co to jest funkcja? Zaczerpnięte z MathSisfun.com.