Funkcje stopnia większe niż dwa (przykłady)

A (wielomianowy) klasy większy niż dwa ma ogólną formę:

f (x) = a₀ + Do₁x +a₂X² +.. .Do_NX^N

Z n = 3, 4, 5,…, nienegatywną liczbą całkowitą i współczynnikami_albo, Do₁… Do_N, które zwykle są liczbami rzeczywistymi.

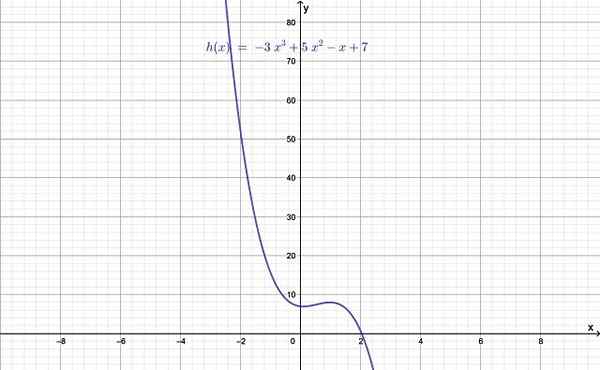Rysunek 1.- Wykres funkcji stopnia większego niż 2. Źródło: f. Zapata.

Stopień funkcji jest podany przez wartość n, największą z wykładników, a z kolei jest większy niż 2. Gdy n = 0 jest funkcją stałą, jeśli n = 1 jest funkcją liniową, a na koniec z n = 2 jest funkcją kwadratową.

Przykłady funkcji większych niż dwie, w zmiennej „x”, są następujące:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

Funkcja f (x) = x³ Jest to najprostsze ze wszystkich funkcji większych niż dwie, a jego stopień to 3. Stopień 3 jest również znany jako funkcja sześcienna. Ze swojej części g (x) to klasa 4, ponieważ jest 4 maksymalnym wykładnikiem.

Wartość n jest bardzo ważna, ponieważ określa ogólną formę wykres. Rzeczywiście, funkcja 3 -negatywna dotknie osi poziomej co najwyżej 3 punkty, jeden z klasy 4 zrobi to co najwyżej w 4 punktach i tak dalej.

Co do niezależnego terminu, w funkcji wielomianowej dowolnego stopnia wskazuje na przecięcie funkcji z osą pionową.

Charakterystyka funkcji wielomianowych większych niż dwa

Domena

Domena funkcji jest zestaw wartości, które pozwalają obliczyć wartości y = f (x). W przypadku funkcji wielomianowych ten zestaw to rzeczywiste liczby N lub zestaw liczb złożonych, jeśli to konieczne, aby rozszerzyć domenę.

Może ci służyć: limity trygonometryczne: jak je rozwiązać, rozwiązane ćwiczenia

Oznacza, że ​​biorąc pod uwagę funkcję wielomianową f (x) = a₀ + Do₁x +a₂X² +.. .Do_NX^N, Zawsze możesz wymienić dowolną liczbę rzeczywistą, przeprowadzić wskazane operacje i uzyskać w rezultacie wartość rzeczywistej y = f (x) real.

Zakres

Jest to zestaw utworzony przez wszystkie uzyskane wartości f (x), to znaczy obrazy, które każda wartość x ma poprzez funkcję f (x). W przypadku funkcji wielomianowych większych niż 2, ten zestaw jest liczb rzeczywistych.

Korzenie funkcji

Są wartościami x, dla których jest wypełnione, że f (x) = 0. Jak wskazano powyżej, stopień funkcji wskazuje maksymalną liczbę korzeni, które może mieć, chociaż nie wszystkie z nich są koniecznie prawdziwe.

Gdy współczynniki funkcji są liczbami rzeczywistymi, rzeczywiste korzenie odpowiadają przecięciom funkcji z osą x.

Przykład 1

Racjonalne korzenie funkcji f (x) = 2x³ - 9x² + 7x + 6 można znaleźć w następującym twierdzeniu:

Jeśli korzeń f (x) = a₀ + Do₁x +a₂X² +.. .Do_NX^N Jest to forma B/C, więc możliwe wartości B są czynnikami a_albo a możliwe wartości C są czynnikami_N.

Dla funkcji przykładu już uproszczone kombinacje to: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Teraz każdy jest testowany na przykład w procedurze podziału syntetycznego. Gdy pozostałość oddziału wynosi 0, sprawdzona wartość jest korzeniem:

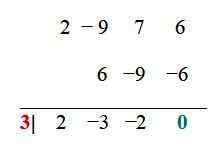
Wartość x₁ = 3 jest korzeniem lub zero funkcji, dlatego (x - 3) jest wspólnym czynnikiem f (x) i można to zapisać jako:

Może ci służyć: jednolite okrąg: funkcje trygonometryczne i aplikacje

f (x) = (x - 3) ∙ (2x² −3x −2)

Pozostałe dwa korzenie to wartości spełniające równanie 2x² −3x −2 = 0. To równanie można rozwiązać poprzez ogólny wzór, kalkulator naukowy lub powtarzanie poprzedniego procesu Tanteo.

Te korzenie to x₂ = 2 i x₃ = - ½, a teraz f (x) można zapisać jako iloczyn trzech czynników:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

Przecięcia f (x) z osą x są punktami: p₁ (3.0), str₂(2.0) i P₃(−½, 0). Wykres funkcji, uzyskany z Geogebra, pokazuje jej skrzyżowania z osą X:

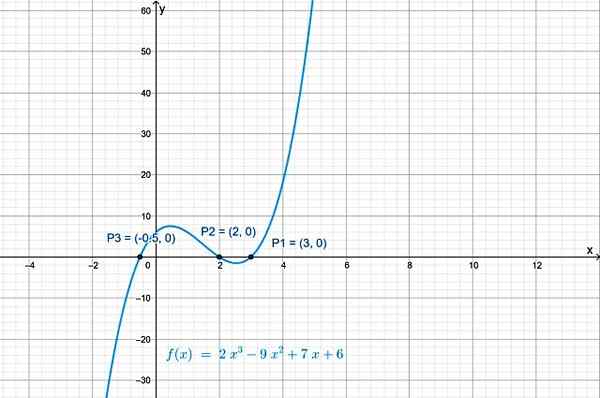Rysunek 2.- Funkcja wielomianowa klasy 3 ma trzy skrzyżowania z osą poziomą. Źródło: f. Zapata.

Skrzyżowanie z osą pionową

Aby znaleźć przecięcie funkcji z osą pionową, musisz znaleźć f (0), co jest po prostu₀.

Przykład 2

Znajdź przecięcie f (x) = 2x³ - 9x² + 7x + 6 Z osą pionową jest bardzo prosty, przy tworzeniu x = 0 w f (x) jest uzyskiwane:

f (x) = 6

A punkt przecięcia funkcji z osą pionową jest P₄(0,6).

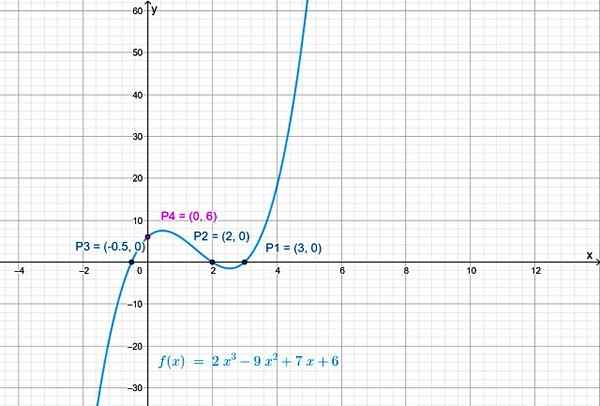Rysunek 3. Przecięcie krzywej z osą pionową powoduje x = 0 w f (x). Źródło: f. Zapata.

Ciągłość

Funkcje wieloparomiczne w ogóle, a w szczególności funkcje wyższych niż 2 są funkcjami ciągłymi w całej ich dziedzinie, oznacza to, że nie mają one skoków, kroków, otworów ani wartości, dla których nie są zdefiniowane. Nie mają też asymptotów, które są pionowe, poziome lub skośne prosto, do których zbliża się funkcja bez ich przekraczania.

Te cechy miękkości i ciągłości są doceniane na wykresach pokazanych powyżej.

Wykres funkcji wyższych niż 2

Wykresy funkcji wyższych niż 2 są ciągłe i miękkie, a ich kształt zależy od stopnia wielomianu.

Może ci służyć: permutacje bez powtórzeń: formuły, demonstracja, ćwiczenia, przykłady

Na przykład, te z ryki klasy 3 ma ujemny znak w terminie o najwyższym stopniu).

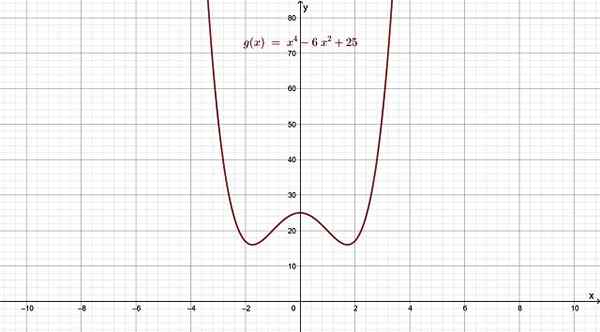Rysunek 4. Funkcja poliinomiczna klasy 4, której wykres przypomina literę w. Źródło: f. Zapata.

W przypadku wartości x od x = 0, zarówno lewej, jak i prawej, funkcja zachowuje się, jak zrobiłby to termin największego stopnia, ponieważ panuje nad innymi, gdy x staje się bardzo duże lub bardzo małe.

Na obrazie, który podąża za funkcją f (x) = 2x³ - 9x² + 7x + 6 z funkcją r (x) = x³ I docenia się, że kształt obu krzywych jest podobny do wartości x, które są daleko od x = 0.

W przypadku dużych wartości x funkcja szybko rośnie, dążąc do +∞, podczas gdy dla ujemnych wartości x funkcja szybko maleje i ma tendencję do ace.

Rysunek 5.- Wszystkie funkcje klasy N zachowują się podobnie, gdy odchodzą od x = 0, zarówno w lewo, jak i w prawo. Źródło: f. Zapata.

Porównując krzywe uregulatora momentu obrotowego (ryc. 4) ze stopniem nieparzystym (ryc. 2), o ile współczynnik towarzyszący najwyższemu terminowi ma ten sam znak, obserwuje się, że krzywe nieparzystego stopnia zaczynają się od „y” ujemnych i ujemnych i ujemnych rosnąć, podczas gdy te o klasie docelowej zaczynają się w „y” pozytywnie i zmniejszają.

Bibliografia

1. Barnett, r. 2000. Pretriculment: Funkcje i grafika. 4. Wydanie. McGraw Hill.
2. Obliczenie.DC. Funkcje wieloparomiczne. Odzyskane z: Obliczanie.DC.
3. Larson, r. 2012. Przedłużanie. 8. Wydanie. Cengage Learning.
4. Stewart, J. 2007. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
5. Varsity Tutorrs. Wykresy funkcji wielomianowych. Źródło: WarsityTorm.com.