Prawdziwa funkcja zmiennej rzeczywistej i jej graficzna reprezentacja

A prawdziwa funkcja zmiennej Weź liczbę należącą do zestawu liczb rzeczywistych i kojarzy go z inną wartością, również prawdziwą, poprzez unikalną zasadę korespondencji. Oznacza to, że liczba rzeczywista, dzięki tej regule, unikalny obraz.

Numeryczne zmienne odlotu są zwykle oznaczone literą X, podczas gdy ich wizerunkiem jest litera i. Z drugiej strony do zasady korespondencji, która je łączy, jest również wywoływana z inną literą alfabetu, taką jak funkcja „F”, chociaż inna można użyć.  W notacji kompaktowej jest napisane:

f: x → y = f (x)

Rysunek 1. Wykres prawdziwej funkcji wielomianowej

Do zmiennej  X nazywa się Zmienna niezależna, podczas I To jest zmienna zależna. Funkcję można wyrazić na kilka sposobów, na przykład poprzez takie stwierdzenie matematyczne:

• f (x) = 2x −3
• H (x) = −3x²
• 

Inną formą wyrażenia jest wykres, który jest bardzo przydatny, ponieważ pozwala docenić zachowanie funkcji jednego spojrzenia. Budowanie wykresu jest bardzo proste przy użyciu kartezjańskiego systemu współrzędnych, w którym rówieśnicy [x, f (x)] są reprezentowani jako punkty w płaszczyźnie. Następnie łączą linię miękką i ciągłą, możesz zobaczyć, jak jest funkcja.

Przykłady

Aby zbudować wykres, możesz uciekać się do tabeli wartości, w których umieszczane są punkty do wykresu. W przypadku zmiennych x wartości należą do domeny funkcji, to znaczy tych, które po wymianie w formule, z kolei pokazują liczby rzeczywiste.

Po wybraniu wartości x określa się jego obraz y = f (x) i w ten sposób uzyskuje się pary punktów [x, f (x)], które będą graficzne.

Może ci służyć: funkcja homograficzna: jak wykres, rozwiązane ćwiczenia

Istnieją pewne punkty, które są ważne i powinny być zawarte w tabeli: te, w których wykres przecina osie współrzędnych, że jeśli istnieją, ponieważ nie wszystkie funkcje je przecinają.

Aby je obliczyć, postępuj w następujący sposób:

-Skrzyżowanie z osą i: x = 0 jest wykonany w wzorze funkcji i obliczana jest odpowiednia wartość.

-Przecięcie z osi x: Y = 0 jest wykonywane, a równanie f (x) = 0 jest rozwiązane.

Następnie rysowany jest system współrzędnych kartezjański i każdy z punktów jest wykreślany, które są następnie połączone miękką i ciągłą linią, jeśli to możliwe.

Przykład 1

Zbuduj tabelę wartości i wykres następującej funkcji:

f (x) = x² −4

Przed rozpoczęciem musisz znaleźć domenę funkcji, która jest zestawem wartości rzeczywistych, dla których funkcja istnieje. Ponieważ jest to funkcja kwadratowa, każda wartość x należąca do liczb rzeczywistych ma prawdziwy obraz, zgodnie z F (x).

Następnie tabelę można zbudować, wybierając dowolną wartość X, a najprostszą rzeczą jest rozpoczęcie od skrzyżowań wykresu z osiami, jeśli tak. Po ich znalezieniu, inne punkty mają na celu ukończenie tabeli.

Dla x = 0

f (0) = -4

Dlatego pierwszym punktem w tabeli jest (0, -4). To jest przecięcie wykresu z osą i.

Dla y = 0

Następnie Y = 0 jest wykonywane i równanie, które wyniki jest rozwiązane:

X² −4 = 0

X² = 4

Rozwiązania tego równania to: x₁= 2 i x₂= -2. Dlatego istnieją dwa skrzyżowania z osą x, które są punktami: (-2,0) i (2.0).

Może ci służyć: Idealne liczby: Jak je zidentyfikować i przykłady

Teraz możesz znaleźć więcej punktów do dodania do tabeli wartości:

Dla x = 1

f (1) = (1)² - 4 = −3

Dla x = - 1

f (−1) = (−1)² - 4 = −3

Dla x =  3

f (3) = (3)² - 4 = 5

Dla x =  -3

f (−3) = (−3)² - 4 = 5

Tabela wartości

Poniższa tabela pokazuje uzyskane punkty, które będą służyć do zbudowania wykresu F (x):

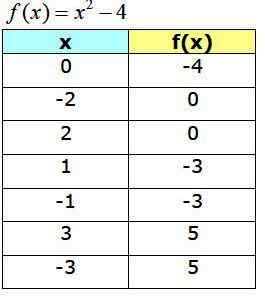Wykres funkcji f (x) = x² −4

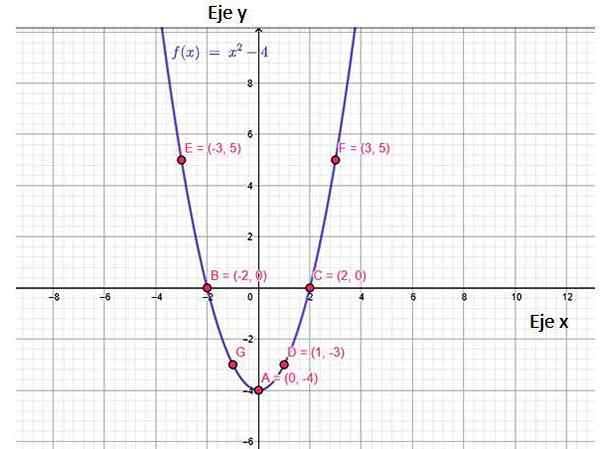Rysunek 2. Funkcja F (x) Wykres funkcji, pokazujący niektóre punkty, które do niego należą, w tym skrzyżowania z osiami. Źródło: f. Zapata, przez Geogebra.

Wykres tej funkcji jest przypowieścią, która otwiera się i ma co najmniej punkt, nazywany wierzchołek, współrzędnych (0, −4). Warto zauważyć, że wartości f (x) zaczynają się od y = -4 do ∞. To jest Zakres funkcji.

Wykresu można stwierdzić, że funkcja jest ciągła, maleje w przedziale (∞∞, 0) i stamtąd wzrasta.

Przykład 2

Posiadanie wykresu funkcji można poznać jej domenę, jej zakres, przecięcia, które ma z osiami i wizualizować jej ogólne zachowanie (wzrost i spadek).

Poniżej znajduje się wykres funkcji wielomianowej:

f (x) = - x⁴+4x²+1

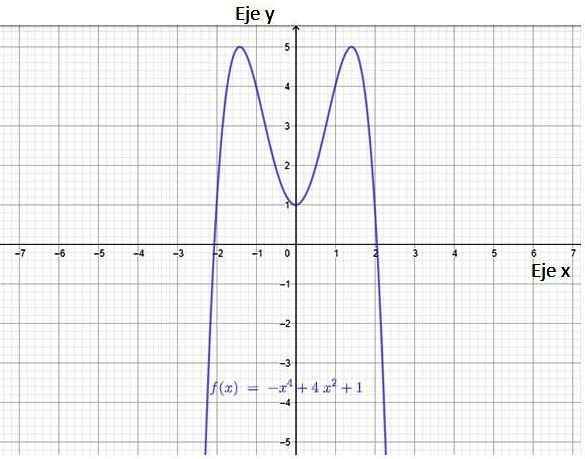Rysunek 3. Wykres funkcji wielomianowej. Źródło: f. Zapata przez Geogebra.

Z obrazu wynika, że ​​funkcja ma dwa skrzyżowania z osą x, punkty (-2,0) i (2.0). Ma również skrzyżowanie z osą y, punkt (0,1).

Domena funkcji wielomianowej jest pełny zestaw liczb rzeczywistych, ostrzega również, że funkcja jest ciągła i ma symetrię wokół osi pionowej. Rzeczywiście można zweryfikować, że ta funkcja jest Symetria dla. Funkcja jest nawet jeśli się spotyka:

Może ci służyć: zielone twierdzenie, demonstracja, aplikacje i ćwiczenia

f (x) = f (-x)

Czytnik może sprawdzić, że zastępując -x w funkcji, nie jest zmieniany.

Istnieją dwa interesujące punkty, które są na wysokości y = 5, to maksymalne wartości funkcji. Zakres tej funkcji, to znaczy zbiór wartości, które zmienna przyjmuje i rozciąga się od -∞ do y = 5 precyzyjnie.

Aby poznać wartości x, którego obraz to y = 5, wartość ta jest zastąpiona w funkcji:

5 = - x⁴+4x²+1

I to równanie jest uzyskiwane:

- X⁴ + 4x² - 4 = 0

Którego roztwory to √2 i + √2. Cóż, funkcja to:

-Rozwój Od x -∞ do x = √2

-Zmniejszenie Od x = √2 do x = 0

-Rozwój Od x = 0 do x = + √2

-Zmniejszenie Od x = + √2 dalej.

Ćwiczenie rozwiązane

Zbuduj wykres następującej funkcji:

f (x) = √ (x-5)

Rozwiązanie

Najpierw musisz określić domenę funkcji, aby wiedzieć, które wartości x można wybrać do zbudowania tabeli. W przypadku proponowanej funkcji kwota w korzeniu musi być zawsze dodatnia lub równa 0, dlatego:

x - 5 ≥ 0

x ≥ 5

Dlatego dla tabeli można wybrać tylko wartości większe lub równe 5. Jeśli chodzi o przecięcia z osi współrzędnych, jedyną możliwością jest robienie y = 0, a następnie x = 5.

Bezużyteczne jest robienie x = 0 dla tej funkcji, ponieważ ta wartość nie należy do domeny.

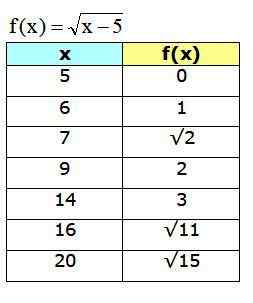
Uzyskany wykres to:

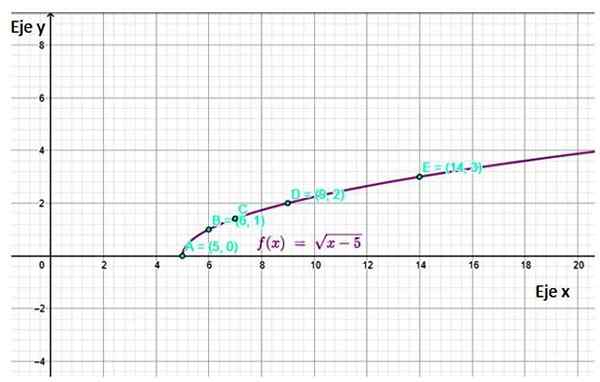Rysunek 4. Wykres funkcji F (x) pokazujący niektóre punkty obliczone w tabeli. Źródło: f. Zapata przez Geogebra.

Bibliografia

1. Strefa e-matem. Rodzaje funkcji. Odzyskany z: Emathzone.com.
2. Hoffman, J.G. Wybór problemów z matematyką. Wyd. SPPHINX.
3. Matematyka jest zabawna. Odniesienie funkcji Commons. Odzyskany z: Mathisfun.com.
4. Requena, ur. Formuły wszechświata. Rodzaje funkcji. Odzyskane z: Universoformulas.com.
5. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.