Funkcja homograficzna Jak wykres, rozwiązane ćwiczenia

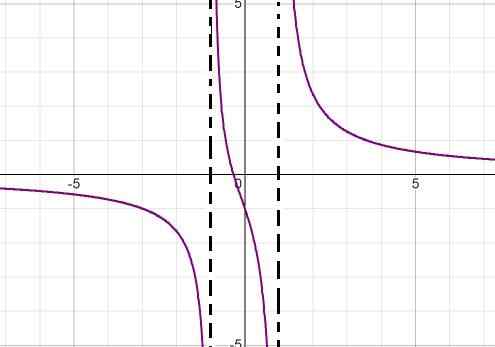
funkcjonowaćHomograficzny lub racjonalny Ón Jest to rodzaj funkcji matematycznej złożonej z podziału dwóch elementów wielomianowych. Posiada formę p (x)/q (x), gdzie q (x) nie może przybierać zerowego kształtu.

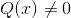
Na przykład wyrażenie (2x - 1)/(x + 3) odpowiada funkcji homograficznej z p (x) = 2x - 1 y q (x) = x + 3.

Źródło: Pixabay.com

Funkcje homograficzne stanowią sekcję badań funkcji analitycznych, traktowanych z podejścia graficznego oraz z badania domeny i zakresu. Wynika to z ograniczeń i fundamentów, które należy zastosować do ich rezolucji.

[TOC]

Co to jest funkcja homograficzna?

Są to racjonalne wyrażenia unikalnej zmiennej, chociaż nie oznacza to, że nie ma podobnego wyrażenia dla dwóch lub więcej zmiennych, gdzie byłoby to już w obecności ciał w przestrzeni, które są posłuszne tych samych wzorców, co funkcja homograficzna na poziomie.

W niektórych przypadkach mają prawdziwe korzenie, ale istnienie asymptotów pionowych i poziomych jest zawsze utrzymywane, a także odstępy wzrostu i zmniejszania. Zwykle występuje tylko jeden z tych trendów, ale istnieją wyrażenia zdolne do pokazania obu w ich rozwoju.

Jego domena jest ograniczona przez korzenie mianownika, ponieważ nie ma podziału między zero liczb rzeczywistych.

Mieszana funkcja homograficzna

Są one bardzo częste w obliczeniach, zwłaszcza różnicowych i kompleksowych, które są konieczne do uzyskania i anty -angel w określonych formułach. Niektóre z najczęstszych są sklasyfikowane poniżej.

N -tyma funkcji homograficznej

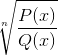
Wyklucza wszystkie elementy domeny, które czynią argument negatywny. Korzenie obecne w każdym wielomianie pokazują wartości zerowe po ocenie.

Wartości te są akceptowane przez radykalne, chociaż należy rozważyć podstawowe ograniczenie funkcji homograficznej. Gdzie Q (x) nie może odbierać wartości zerowych.

Może ci służyć: funkcje transcendentne: typy, definicja, właściwości, przykłady

Rozwiązania interwałowe należy przechwycić:

Aby osiągnąć przecięcia, można zastosować metodę znaku, między innymi.

Logarytm funkcji homograficznej

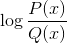
Wyklucza wartości domeny, które rzucają negatywne odstępy i zera. Ponieważ zera są już wykluczone z mianownika, rozwiązania: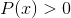

Powszechne jest również znalezienie obu wyrażeń w jednym, między innymi możliwymi kombinacjami.

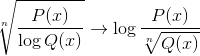
Jak wykreślić funkcję homograficzną?

Funkcje homograficzne odpowiadają graficznie z hiperbolą w płaszczyźnie. Które są transportowane poziomo i pionowo zgodnie z wartościami definiującymi wielomiany.

Istnieje kilka elementów, które musimy zdefiniować, aby wykresować funkcję racjonalną lub homograficzną.

Nieruchomość

Pierwszym będą korzenie lub zera funkcji p i q.

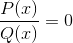
Osiągnięte wartości zostaną oznaczone na osi x grafiki. Wskazując przecięcia wykresu z osą.

Pionowa asymptota

Odpowiadają linkom pionowym, które wyznaczają wykres zgodnie z obecnymi trendami. Dotykają osi x w wartościach, które powodują zero mianownika i nigdy nie będą dotknięte wykresem funkcji homograficznej.

Asymptota pozioma

Reprezentowany przez poziomą linię ściegów, wyznaczył limit, dla którego funkcja nie zostanie zdefiniowana w dokładnym punkcie. Trendy będą obserwowane przed i po tej linii.

Aby go obliczyć, musimy zastosować metodę podobną do metody L'Hopital, stosowanej do rozwiązywania limitów funkcji racjonalnych, które mają tendencję do nieskończoności. Należy pobrać współczynniki najwyższych mocy w licznikach i mianownik funkcji.

Na przykład następujące wyrażenie ma poziomą asymptotkę przy y = 2/1 = 2.

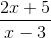
Odstęp wzrostu

Wartości uporządkowanego będą miały trendy oznaczone na wykresie z powodu asymptotów. W przypadku wzrostu funkcja wzrośnie z wartości, gdy elementy domeny od lewej do prawej są oceniane.

Może ci służyć: 60 dzielników

Zmniejszanie interwału

Uporządkowane wartości spadną w miarę oceny elementów domeny od lewej do prawej.

Skoki znalezione w wartościach nie będą brane pod uwagę w miarę wzrostu lub zmniejszenia. Dzieje się tak, gdy wykres jest blisko pionowego lub poziomego.

Przecięcie z y

Powodując zero wartość x, to przecięcie z osą rzędnych. Jest to bardzo przydatny fakt do uzyskania wykresu funkcji racjonalnej.

Przykłady

Zdefiniuj wykres następujących wyrażeń, znajdź jego korzenie, pionowe i poziome asymptoty, wzrost i zmniejszenie odstępów i przecięcia z osą uporządkowanej.

Ćwiczenie 1

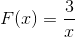
W wyrażeniu brakuje korzeni, ponieważ ma stałą wartość w licznikach. Ograniczenie do zastosowania będzie x różni się od zera. Z poziomą asymptotem przy y = 0 i asymptotto pionowym przy x = 0. Nie ma punktów przecięcia z osą i.

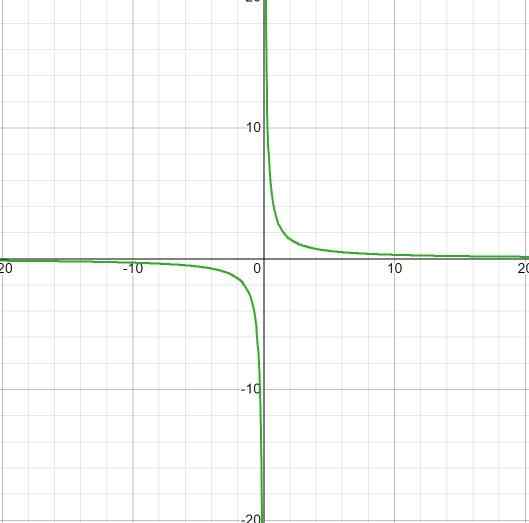
Obserwuje się, że nie ma przedziałów wzrostu, nawet przy skoku z mniej do bardziej nieskończonego w x = 0.

Przedział zmniejszania wynosi

Id: (-∞; o) u (0, ∞)

Ćwiczenie 1.2

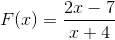
2 wielomiany są obserwowane jak w początkowej definicji, więc postępujemy zgodnie z ustalonymi krokami.

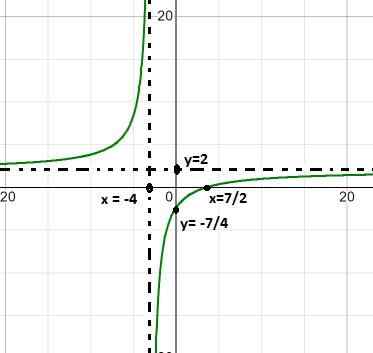
Znaleziony root to x = 7/2, który wynika z wyrównania funkcji.

Pionowa asymptota jest przy x = - 4, która jest wartością wykluczoną z domeny ze względu na warunek funkcji racjonalnej.

Asymptota pozioma jest w y = 2, po podzieleniu 2/1, współczynniki zmiennych klasy 1.

Ma skrzyżowanie z uporządkowanymi w Y = - 7/4. Wartość znaleziona po wyrównaniu x do zera.

Może ci służyć: ułamek równoważny 3/5 (rozwiązanie i wyjaśnienie)

Funkcja stale rośnie, ze skokiem z większej do mniej nieskończonej wokół korzenia x = -4.

Jego przedział wzrostu wynosi (-∞, - 4) u ( - 4, ∞).

Gdy wartość x jest zbliżona do mniej nieskończonej, funkcja pobiera wartości bliskie 2. To samo dzieje się, gdy X zbliża się do bardziej nieskończonych.

Ekspresja zbliża się do bardziej nieskończonego, gdy oceniono w - 4 po lewej i mniej nieskończonej, gdy oceniono w - 4 po prawej stronie.

Ćwiczenie 2

Obserwuje się wykres następującej funkcji homograficznej:

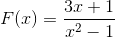
Opisz ich zachowanie, korzenie, pionowe i poziome asymptoty, przedziały wzrostu i zmniejszania oraz przecięcie z uporządkowaną osą.

Mianownik ekspresji wskazuje poprzez uwzględnienie różnicy kwadratów (x + 1) (x - 1) wartości korzeni. W ten sposób oba pionowe asymptoty można zdefiniować jako:

x = -1 i x = 1

Asymptota pozioma odpowiada osi odciętej, ponieważ główną moc jest w mianowniku.

Jego jedyny korzeń jest zdefiniowany przez x = -1/3.

Wyrażenie zawsze maleje od lewej do prawej. Zbliża się do zera, gdy ma tendencję do nieskończoności. Mniej nieskończenie, gdy zbliża się do -1 po lewej stronie. Bardziej nieskończone, gdy zbliża się do -1 po prawej stronie. Mniej nieskończone, gdy zbliża się do 1 po lewej i bardziej nieskończoności, zbliżając się do 1 po prawej stronie.

Bibliografia

1. Przybliżenie za pomocą funkcji racjonalnych. Donald J. Nowego człowieka. American Mathematical Soc., 31 grudnia. 1979
2. Funkcje oceny ortogonalnej. University of La Laguna Teneryfe Adhemar Bultheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav NJstad. Cambridge University Press, 13 lutego. 1999
3. Przybliżenie oceny rzeczywistych funkcji. P. P. Petreshev, Vasil Atanasov Popov. Cambridge University Press, 3 marca. 2011
4. Funkcje algebraiczne. Gilbert Ames Bliss. Couer Corporation, 1 stycznia. 2004
5. Hiszpański magazyn Towarzystwa Matematycznego, 5-6 tomów. Hiszpańskie Towarzystwo Matematyczne, Madryt 1916