Złapane charakterystyka funkcji, przykłady, ćwiczenia

Funkcja rozłożona y = s (x) jest funkcją zdefiniowaną w kawałkach lub przez części, tak że w skończonym odstępie [a, b] ma skończoną liczbę nieciągłości, które nazwiemy x₀ < x₁ < x₂ <… . x_N.  W każdym otwartym przedziale (x_Siema , X_I+1) i ma stałą wartość s_Siema, Z nieciągłości -Saltos- w punktach x_Siema.

Wykres wynikający z takiej funkcji składa się z kroków lub kroków. Spójrzmy na przykład poniżej:

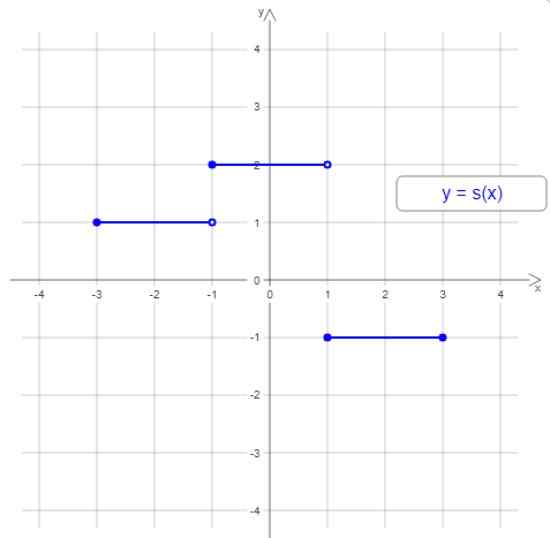
Rysunek 1. Przykład funkcji rozłożonej. Źródło: Wikimedia Commons.

Wykres tej stopniowej funkcji ma trzy kroki lub rozłożone odstępy, ale ogólnie rzecz biorąc. Szerokość kroków może być inna, a schody nie zawsze rosną lub maleją.

Złożona funkcja przykładu można zapisać, określając szerokość i wysokość każdego kroku, jak ten:

[TOC]

Charakterystyka stopniowej funkcji

-Funkcja odbiera swoją nazwę przez wykres w postaci kroków, podanych przez segmenty, które ją komponują. Każdy segment ma część domeny funkcji, aw każdej z niej funkcja jest stała.

-Domena funkcji zatoczonej są wartości, które należą do interwału, dla którego jest zdefiniowana: [a, b], podczas gdy zakres jest składany przez wartości s_Siema wysokości kroków.

W przykładzie na rycinie 1 domena jest przedział [-3,3], a zakres to wartości -1, 1 i 2.

-Funkcja rozłożona jest ciągła, z wyjątkiem wartości, które wyznaczają każdy krok, punkty x_Siema.

-Funkcje escalonada można dodać i mnożyć, aby spowodować nowe funkcje stopniowe.

-Jego pochodna wynosi 0 dla punktów, w których jest zdefiniowana, ponieważ w nich funkcja jest stała. Ze swojej strony pochodna nie istnieje w nieciągłości.

-Całka stopniowej funkcji s (x) między Do I B Istnieje i odpowiada sumie obszarów prostokątów szerokości x_Siema- X_I-1 i wysokość s_k, równe krokowi.

Może ci służyć: niezależne wydarzenia: demonstracja, przykłady, ćwiczenia

Ponieważ obszar prostokąta jest produktem podstawy według wysokości, musimy:

Przykłady rozłożonych funkcji

W ramach rozłożonych funkcji istnieje kilka rodzajów, na przykład funkcje Cała część i funkcja Jednostki krok, a także różne rozłożone funkcje opisujące wspólne sytuacje, takie jak stawki wielu usług. Spójrzmy na kilka przykładów:

- Przykład 1: Całe strony

Funkcja całej części często używa podwójnego wspornika:

f (x) = [[x]]

I jest zdefiniowany jako funkcja, która przypisuje się do każdej liczby rzeczywistej najbliższej lub mniejszej liczby całkowitej, ignorując każdą dziesiętną liczbę. Jak to możliwe, mamy:

Funkcja dachu lub nieba

Przypisuje się do każdej wartości domeny najbliższą liczbą całkowitą przez nadmiar. Na przykład:

[[+2.56]] = 3

Część dziesiętna, która jest 0, jest ignorowana.56 i przypisana jest najbliższa liczba całkowita, która jest większa niż 2.

Inny przykład:

[[-4.2]]= -3

Ponownie część dziesiętna 0 jest pomijana.2 i najwyższa największa liczba całkowita bliżej -4 jest traktowana jako wartość funkcji, która wynosi -3.

Na poniższym rysunku znajduje się wykres funkcji sufitu, zauważ, że krok jest ograniczony przez małe puste okrąg po lewej stronie i jeden pełny w prawo, ponieważ dowolna liczba przedziałów, największa liczba całkowita jest przypisana między końcami między końcami między końcami między kończy się między końcami interwału.

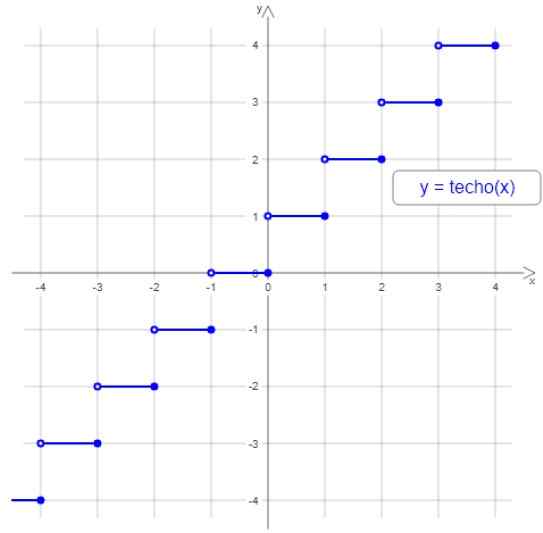Rysunek 2. Funkcja dachu lub nieba. Źródło: Wikimedia Commons.

Na przykład wszystkie wartości między 3 a 4 przypisane są całe 4, które są między -2 i -1, są przypisane -1 i tak dalej.

Funkcja podłogi lub gleby

Przypisuje się do każdej wartości domeny, domyślnie najbliższy numer całkowitą. Przykładami tej funkcji to:

Może ci służyć: ile dziesiątych jest w jednostce?

[[+3.7]] = 3

[[-1.5]] = -2

[[π]] = 3

Obie funkcje są ciągłe, z wyjątkiem liczb całkowitych, w których prezentowane są skoki i są stałe dla wartości między liczbami całkowitych K i K+1.

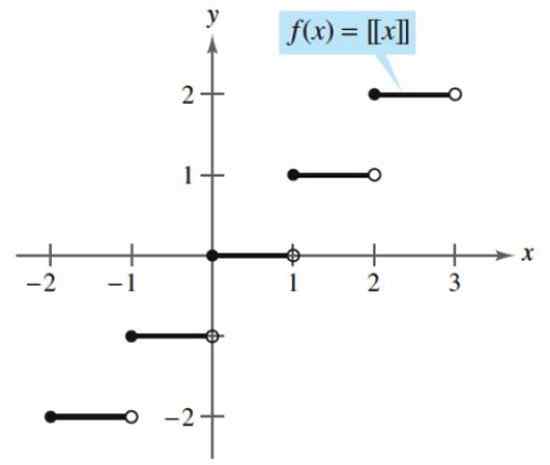Rysunek 3. Funkcja podłogi lub gleby. Źródło: Larson, r. Obliczanie zmiennej.

- Przykład 2

W mieście taksówka wynosi 3.65 USD za pierwsze 100 m. I na każde 100 m to 0.18 USD, będąc limitem na trasę 50 km.

Pożądane jest ustalenie funkcji, która odnosi trasę w metrach z kosztem usługi przez $, która musi mieć ten formularz:

f (x) = 3.65 + 0.18. [[x /100]] $

Gdzie funkcja całej części może być funkcja nieba, do której dodawana jest szybkość podstawowa 3.65 USD. Na przykład, jeśli chcemy wiedzieć, ile zostanie zapłacone za podróż 6.25 km = 6250 m, będziemy mieli:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 15.65 USD

Jeśli taksówki wybierze funkcję podłogową, klient zapłaciłby nieco mniej za podróż:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 14.65 USD

Rozwiązane ćwiczenia

- Ćwiczenie 1

Połączenia na duże odległości między miastami A i B Koszt 0.40 10 minut. Po tym okresie frakcja lub dodatkowa minuta jest warta 0.05 $.

Wyraź koszt C (t) połączenia, które trwa określoną ilość minut.

Rozwiązanie

Możemy wyrazić tę funkcję, jeśli przeanalizujemy, co dzieje się z każdą opcją na czas trwania połączenia:

Przez t ≤ 10 minut

Kiedy t, który jest czasem, w którym połączenie trwa, jest mniejsze lub równe 10 minut, otrzymuje zapłatę 0.40 USD.

Może ci służyć: 2 -Digit Dywizje rozwiązane

Dlatego:

f (t) = 0.40 USD za t w zestawie od 0 do 10 minut.

Mamy już część funkcji.

Przez t> 10 minut

Entero T. Case

Zobaczmy teraz, co się stanie, gdy przekroczony jest czas t = 10 minut: może się zdarzyć, że nadmiar jest liczbą całkowitą, na przykład, że rozmowa trwa dokładnie 11, 12, 13, 14 minut lub więcej. W takim przypadku kwota połączenia będzie:

f (t) = 0.40 + 0.05 (T-10) $, dla t ponad 10 minut, z całkowitym t.

To znaczy, że w tym przypadku: t = 11, 12, 13, 14, 15 ... minuty.

Załóżmy na przykład, że rozmowa trwa dokładnie 15 minut, koszt będzie:

f (15) = 0.40 + 0.05 (15-10) $ = 0.65 USD

Przypadek dziesiętna

Na koniec rozważ przypadek, w którym połączenie trwa przez pewien czas z częścią dziesiętną. Załóżmy na przykład, że połączenie trwa 15 minut i 45 sekund, co wynosiłoby dziesiętne 15 lat.75 minut.

Możemy to wyrazić w kategoriach całej części typu podłogi, zakładając, że firma chce przynieść więcej korzyści klientowi lub niebo:

f (t) = 0.40 + 0.05 ⋅ [[T-9]] $

Zobaczmy, co klient zapłaciłby, gdyby to była funkcja podłogowa:

F (15.75) = 0.40 + 0.05 ⋅ [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 6 $ = 0.70 USD.

Lub jako funkcja nieba, w takim przypadku koszt byłby:

F (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 7 $ = 0.75 $.

Funkcja i grafika

Jako funkcja zdefiniowana przez części to:

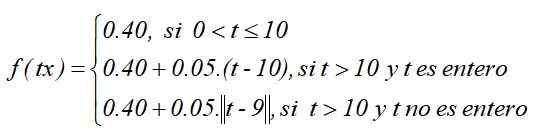
Wykres funkcji byłby taki, zakładając, że wybrano całą funkcję typu sufitu:

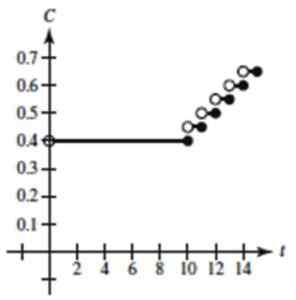Rysunek 4. Wykres stopniowej funkcji ćwiczenia rozwiązanego 1. Źródło: Larson, r. Obliczanie zmiennej.

- Ćwiczenie 2

Oblicz całkę ∫s (x) dx między -3 i 3 stopniowej funkcji:

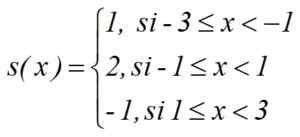
Rozwiązanie

Zastosujemy definicję całki funkcji zatoczonej:

Dlatego integralną poszukiwaną jest:

I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1] = 2+4-2 = 4

Bibliografia

1. Jiménez, r. 2006.Funkcje matematyczne. Edukacja Pearsona.
2. Larson, r. 2010. Obliczanie zmiennej. 9na. Wydanie. McGraw Hill.
3. Matematyka IV. Funkcje. Odzyskane z: COBAQROO.Edu.MX.
4. Wikipedia. Cała część funkcji. Odzyskane z: jest.Wikipedia.org.
5. Wikipedia. Funkcja rozłożona. Odzyskane z: jest.Wikipedia.org.