Wynikowa siła, w jaki sposób obliczone i rozwiązane ćwiczenia

siła wynikły Jest to suma wszystkich sił, które działają na tym samym ciele. Gdy ciało lub obiekt podlega działaniu kilku sił jednocześnie, występuje efekt. Działające siły można zastąpić jedną siłą, która wytwarza ten sam efekt. Ta unikalna siła jest wynikową siłą znaną również jako siła netto i jest reprezentowana z symbolem F_R .

Efekt, jaki wytwarza F_R Będzie zależeć od jego wielkości, kierunku i znaczenia. Fizyczne wielkości, które mają kierunek i znaczenie to wielkości wektorowe.

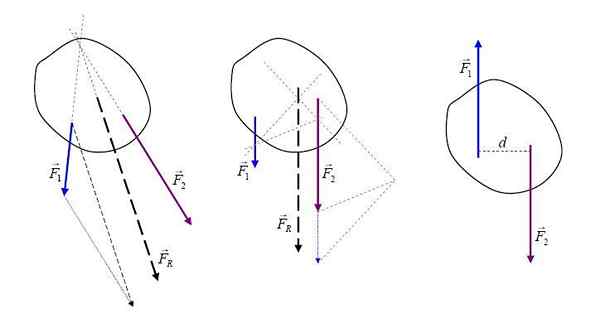Powstałe siły. Przez Ilevanat (https: // commons.Wikimedia.org/wiki/plik: rejultanta.JPG), z Wikimedia Commons

Będąc siłami, które działają na wielkości ciała i wektora, wynikowa siła F_R  Jest to suma wektorowa wszystkich sił i może być reprezentowana graficznie ze strzałką, która wskazuje na jego kierunek i znaczenie.

Przy powstałej sile problem ciała dotkniętych kilkoma siłami jest uproszczony poprzez zmniejszenie go do jednej siły działającej.

[TOC]

Formuła

Matematyczna reprezentacja powstałej siły jest wektorem letnim sił.

 F_R= ∑F          (1)

 ∑F = f₁+ F₂+ F₃+.. F_N           (2)

F_R= Wynikowa siła

∑F = Suma sił

N= Liczba sił

Powstała siła może być również reprezentowana z równaniem drugiego prawa Newtona.

   F_R= m.Do          (3)

M= Masa ciała

a = przyspieszenie ciała

Jeśli równanie (1) zostanie zastąpione w równaniu (3) Uzyskuje się następujące równania:

∑F = m.Do          (4)

F₁+ F₂+ F₃+.. F_{N =} M.Do          (5)

Wyrażenia matematyczne (4) i (5) dostarczają informacji o statusie ciała poprzez uzyskanie przyspieszenia wektora Do.

Jak obliczana jest siła wynikowa?

Powstała siła uzyskuje się przy stosowaniu drugiego prawa Newtona, które ustanawia następujące:

Może ci służyć: siły odległości

Siła netto działająca na ciało jest równa iloczynowi jego masy przez przyspieszenie, które nabywa. (Równanie (3))

Przyspieszenie ciała będzie miało kierunek przyłożonej siły netto. Jeśli wszystkie siły działające w ciele są znane, wystarczy, aby dodać je wektorowo, aby uzyskać wynikową siłę. Podobnie, jeśli powstała siła jest znana, wówczas podzieliłaby ją przez ciało ciała, aby uzyskać jego przyspieszenie.

Jeśli powstała siła jest nieważna, ciało jest w spoczynku lub stałej prędkości. Jeśli powstała siła działa na ciało, pojedyncza siła jest równa tej siła F_R=F.

Gdy kilka sił działa na tym samym ciele, należy wziąć pod uwagę elementy wektorowe siły, a jeśli siły te są równoległe, czy nie.

Na przykład, jeśli poziomo przesuniemy książkę umieszczoną na stole. Siły w kierunku poziomym są jedynymi, które zapewniają przyspieszenie ciała. Pionowa siła netto na książce wynosi zero.

Jeśli przyłożona siła na książce ma skłonność do poziomej płaszczyzny tabeli, siła jest pisana na podstawie elementów pionowych i poziomych.

Wynikły sił równoległych 

Równoległe siły, które działają na ciele, to siły, które działają w tym samym kierunku. Mogą mieć dwa rodzaje równego sensu lub w przeciwnym kierunku.

Gdy siły działające na ciele mają ten sam kierunek i ten sam sens lub są w przeciwnym kierunku, uzyskana siła jest uzyskiwana przez wykonanie suma algebraiczna wartości liczbowych sił.

Może ci służyć: przepływ pola elektrycznego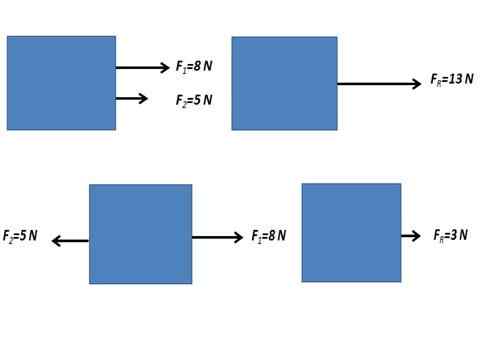Siła wynikająca z dwóch sił równoległych.

Siły nierównoległe

Gdy siły nierównoległe zostaną przyłożone do ciała, powstałe siły będą miały prostokątne i pionowe elementy. Wyrażenie matematyczne do obliczenia siły netto jest:

F_R²= (∑ f_X)²+(∑ f_I)²            (6)

Więc θ_X= ∑ f_I / ∑ f_X         (7)

∑ f_X  i ∑ f_X= Suma algebraiczna komponentów X I I sił stosowanych

θ_X= kąt, który tworzy wynikową siłę F_R Z osą X

Należy zauważyć, że siła wynikająca z wyrażenia (6) nie jest podświetlona w odważnej liście i dzieje się tak, ponieważ wyraża tylko wartość numeryczną. Adres jest określony przez kąt θ_X.

Wyrażenie (6) jest ważne dla sił działających w tej samej płaszczyźnie. Gdy siły działają w przestrzeni, komponent jest brany pod uwagę z siły, jeśli praca z prostokątnymi komponentami.

Rozwiązane ćwiczenia

1. Określ siły wynikające z ciała, które podlega następującym siłom pokazanym na obrazie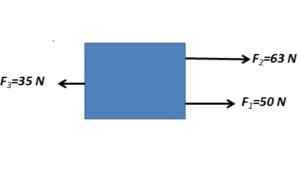

Siły równoległe są dodawane w tym samym sensie i odejmują siłą równoległą w przeciwnym kierunku

F_R= 63 N + 50 N - 35 N = 78N

Powstała siła ma wielkość 78N z kierunkiem poziomym.

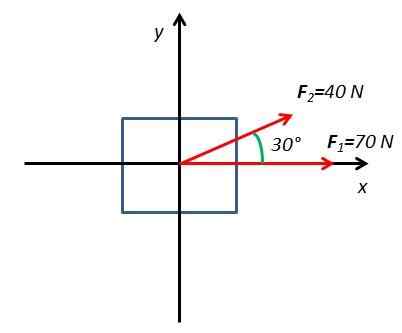
2.Obliczyć siłę wynikającą z ciała pod wpływem dwóch sił F_{1 I} F₂. Siła F₁ Ma wielkość 70N i jest stosowany poziomo. Siła F₂ Ma wielkość 40N i jest stosowany pod kątem 30 ° w odniesieniu do płaszczyzny poziomej.

Aby rozwiązać to ćwiczenie, narysowany jest schemat wolnego ciała z osi współrzędnych X I I

Wszystkie komponenty są określone X I I sił działających na ciele. Siła F₁ Ma tylko poziom poziomy na osi X. Siła F₂ Ma dwa komponenty F_2x  i f_{2 i} które są uzyskiwane z funkcji sinusoidalnych i cosinusowych kąta 30.

Może ci służyć: tarcie: typy, współczynnik, obliczenia, ćwiczenia

F_1x = F₁=70n

F_2x = F₂ Cos 30 ° = 40 n.Cos 30 ° = 34,64N

F_1Y = 0

F_{2 i}= F₂ bez 30 ° = 40 bez 30 ° = 20n

∑ f_X =70N+34,64N = 104,64N

∑ f_I=20n+0 = 20n

Po ustaleniu powstałych sił na osi X I I Uzyskuje się wartość liczbową siły powstałej.

F_R²= (∑ f_X)²+(∑ f_I)²

Powstała siła to pierwiastek kwadratowy letniej suma składników sił

F_R= √ (104,64N)²+(20n)²

F_R= 106,53N

Kąt, który tworzy wynikową siłę F_R Jest to uzyskiwane z następującego wyrażenia:

θ_X= Tan^-1(∑ f_I / ∑ f_X)

θ_X= Więc^-1(20n / 104,64N) = 10,82 °

Powstała siła F_R Ma wielkość 106,53N i ma kierunek określony przez kąt 10,82 °.

Bibliografia

1. Dola, G, Duffy, M i percival. Fizyka. Hiszpania: Heinemann, 2003.
2. Avison, J H. Świat fizyki. Indie: Thomas Nelson and Sons, 1989.
3. Pinsent, m. Proces fizyczny. Wielka Brytania: Nelson Thomas, 2002.
4. Yadav, s k. Mechanika inżynieryjna. Delhi: Discovery Publishing House, 2006.
5. Serway, r a i klejnot, j w. Fizyka dla naukowców i inżynierów. Kalifornia, USA: Brooks/Cole, 2010.