Siła elastyczna to, co polega na formułach i ćwiczeniach

siła elastyczna Jest to siła, którą obiekt wywiera, aby oprzeć się zmianie swojej formy. Objawia się w obiekcie, który ma tendencję do odzyskiwania swojej formy, gdy jest pod działaniem siły deformacji.

Siła sprężystość jest również nazywana siłą odbudowującą, ponieważ sprzeciwia się deformacji, aby zwrócić obiekty do pozycji równowagi. Przeniesienie siły sprężystej odbywa się przez cząstki, które integrują obiekty.

Elastyczna siła wiosny

Na przykład, gdy metaliczna sprężyna jest ściśnięta, siła, która popycha cząsteczki sprężyny, wywiera się poprzez zmniejszenie separacji między nimi, jednocześnie, odporność na pchanie cząstek wywiera siłę sprzeczną z kompresją.

Jeśli zamiast ściskają sprężynę, jest wyrzucany, rozciąganie, cząstki, które ją integrują, są bardziej oddzielone. Podobnie cząstki odporne na oddzielenie siły sprzecznej z rozciąganiem.

Obiekty, które mają właściwość odzyskiwania pierwotnej formy przez przeciwną siłę deformacji, nazywane są obiektami sprężystymi. Sprężyny, gumy sprężyste i elastyczne sznurki są przykładami elastycznych obiektów.

[TOC]

Jaka jest siła elastyczna?

Siła elastyczna (F_k) Jest to siła, którą obiekt wywiera na odzyskanie stanu naturalnej równowagi, ponieważ dotknęła to siła zewnętrzna.

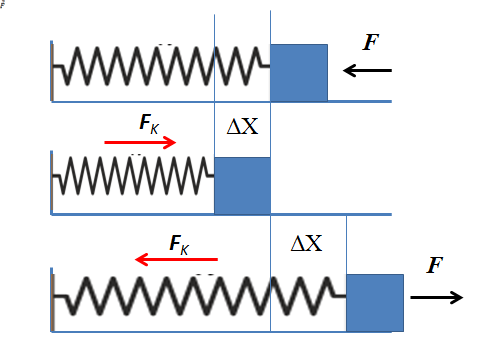
Aby przeanalizować siłę sprężystą, zostanie uwzględniony idealny system masy sprężyny, który składa się z poziomej sprężyny z zastrzeżeniem jednego końca na ścianie, a na drugim końcu bloku nikczemnej masy. Inne siły działające w systemie, takie jak tarcie lub siła grawitacji.

Może ci służyć: Druga równowaga Warunek: wyjaśnienie, przykłady, ćwiczenia

Jeśli na cieście wykonywana jest siła pozioma, skierowana w kierunku ściany, jest ona przenoszona do sprężyny ściskającej. Sprężyna przesuwa się z pozycji równowagi w kierunku nowej pozycji. Ponieważ obiekt ma tendencję do zachowania równowagi, siła sprężystej przejawia się wiosną, która sprzeciwia się przyłożonej sile.

Przemieszczenie wskazuje, jak bardzo odkształcona sprężyna i siła sprężysta jest proporcjonalna do tego przemieszczenia. Gdy sprężyna jest ściśnięta, zmienność pozycji rośnie, a tym samym zwiększa siłę sprężystą.

Im bardziej sprężyna jest ściśnięta, tym większa siła opozycyjna wywiera się, aż osiągnie punkt, w którym przyłożona siła i siła sprężystości są zrównoważone, w konsekwencji system masy sprężyny przestaje się poruszać. Przestań stosować siłę, jedyną siłą działającą jest siła sprężysta. Siła ta przyspiesza sprężynę w kierunku sprzecznym z odkształceniem, aż do odzyskania stanu równowagi.

W ten sam sposób, w jaki występuje podczas rozciągania wiosny obserwując ciasto poziomo. Sprężyna jest rozciągana i natychmiast wywiera siłę proporcjonalną do przemieszczenia przeciwnego rozciągania.

Formuły

Formuła siły sprężystej wyraża prawo Hooke. Prawo to określa, że ​​liniowa siła sprężysty wywierana przez obiekt jest proporcjonalna do przemieszczenia.

F_k = -K.ΔS         [1]

F_k = Siła elastyczna

k = Stała proporcjonalności

ΔS = Przemieszczenie

Gdy obiekt porusza się poziomo, jak w przypadku sprężyny podlegającej ścianie, przemieszczenie jest ΔX, Wyrażenie prawa Hooke'a jest napisane:

F_k = -K.ΔX        [2]

Może ci służyć: zbieżne obiektyw: cechy, typy i ćwiczenia rozwiązane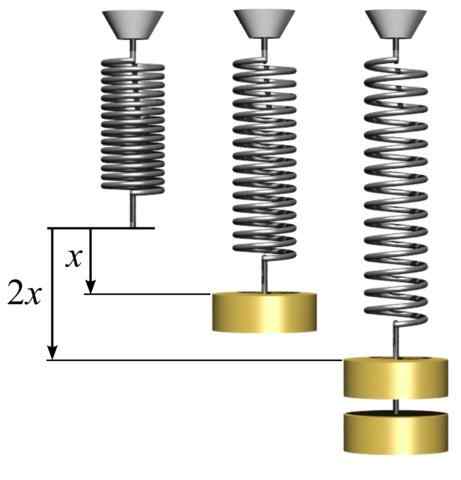Prawo Hooke. Siła elastyczna proporcjonalna do rozciągania. [Przez svjo (https: // commons.Wikimedia.org/wiki/plik: Hookes-Law-Springs.Png)]

Znak ujemny w równaniu wskazuje, że siła sprężysty sprężyny znajduje się w przeciwnym kierunku do siły, która spowodowała przemieszczenie. Stała proporcjonalności k Jest to stała, która zależy od rodzaju materiału, do którego utworzona jest sprężyna. Jedność stałej k Jest N/m.

Obiekty sprężyste mają granicę elastyczności, która będzie zależeć od stałej deformacji. Jeśli rozciąga się poza limit sprężystości, odkształci się na stałe.

Równanie [1] i [2] dotyczy małych przemieszczeń sprężyny. Gdy przemieszczenia są większe, terminy są dodawane o większej mocy ΔX.

Energia kinetyczna i energia potencjalna odnosiły się do siły sprężystej

Siła sprężysta działa na sprężynie, przesuwając ją w kierunku pozycji równowagi. Podczas tego procesu wzrasta energia potencjalnej masy sprężynowej. Energia potencjalna spowodowana pracą wykonaną przez siłę sprężystą wyraża się w równaniu [3].

U = ½ k .  Δx²[3]

Energia potencjalna jest wyrażana w dżuli (J).

Przestań stosując siłę deformacji, sprężyna przyspiesza do pozycji równowagi poprzez zmniejszenie energii potencjalnej i zwiększenie energii kinetycznej.

Energia kinetyczna układu masy sprężynowej, gdy pozycja równowagi osiąga równanie [4].

I_k= ½ m.v²[4]

M = masa

v = Sprężyna

Aby rozwiązać system masy sprężynowej, nakłada się drugie prawo Newtona, biorąc pod uwagę, że siła sprężysta jest siłą zmienną.

Praktyczne ćwiczenia przykładów

Uzyskanie siły odkształcenia

Ile siły jest konieczne, aby zastosować do sprężyny do rozciągania 5 cm, jeśli stała sprężyna wynosi 35N/m?

Może ci służyć: przyspieszenie grawitacji: co to jest, jak jest mierzone i ćwiczy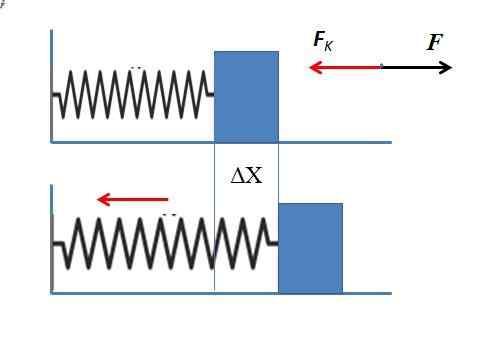Elastyczna siła sprężyny, która rozciąga się na 5 cm

Ponieważ ustalana jest siła zastosowania do siły sprężystej F_k Zakładając, że sprężyna jest rozciągnięta poziomo. Wynik nie wymaga znaku ujemnego, ponieważ siła aplikacyjna jest potrzebna tylko.

Prawo Hooke

F_k = -K.Δx       

Stała k wiosny 35N/m.

Δx = 5 cm = 0,05 m

F_k = -35n/m . 0,05 m

F_k = - 1,75N = - F

Potrzebne 1,75 n siły do ​​deformowania sprężyny 5 cm.

Uzyskanie stałej deformacji

Jaka jest stała deformacji sprężyny, która się rozciąga 20 cm przez działanie siły 60n?

Δx =20 cm = 0,2 m

F = 60n

F_k = -60n = - f

K = - F_k / Δx

  = -(-60n)/0,2 m

K = 300 N/m

Stała sprężyna jest 300N/m

Uzyskanie energii potencjalnej

Jaka jest energia potencjalna, której celem jest praca wykonana przez elastyczną siłę sprężyny sprężonej 10 cm A jego stała deformacji jest 20n/m?

ΔX =10 cm = 0,1 m

K = 20 N/m

F_k = -20n/m . 0,1M

F_k = -200N

Siła sprężystej wiosny jest -200n.

Siła ta działa na sprężynie, aby przesunąć ją w kierunku pozycji równowagi. Podczas wykonywania tej pracy wzrasta energia potencjalna systemu.

Energia potencjalna jest obliczana za pomocą równania [3]

U = ½ k .  Δx²

U = ½ (20n/m) . (0,1 m)²

U = 0,1 Joules

Bibliografia

1. Kittel, C, Knight, W D i Ruderman, M A. Mechanika. US: MC Graw Hill, 1973, t. Siema.
2. Rama Reddy, K, Badami, S B i Balasubramanian, V. Oscylamenty i fale. Indie: University Press, 1994.
3. Murphy, J. Fizyka: ustalenie właściwości materii i energii. New York: Britannica Educational Publishing, 2015.
4. Giordano, n j. Fizyka uczelni: rozumowanie i relacje. Kanada: Brooks/Cole, 2009.
5. Walker, J, Halliday, D i Resnick, R. Podstawy fizyki. US: Wiley, 2014.