Współczynnik i przykłady tarcia lepkiego (siły)

lepkie tarcie Powstaje, gdy stały obiekt porusza się na środku gazu płynu -und lub cieczy-. Można go modelować jako siłę proporcjonalną do ujemnej prędkości obiektu lub kwadratowego.

Zastosowanie jednego lub drugiego modelu zależy od określonych warunków, takich jak rodzaj płynu, w którym obiekt jest przenoszony i czy jest bardzo szybki. Pierwszy model jest znany jako Opór liniowy, i w nim wielkość lepkiego tarcia f_dotykać Jest podany przez:

F_dotykać = ΓV

Rysunek 1. Paracharidystów doświadczają siły lepkiej podczas pochodzenia, ponieważ powietrze oferuje opór. Źródło: Pixabay.

Tutaj γ jest stałą proporcjonalności lub współczynnika lepkiego tarcia, a v jest szybkością obiektu. Dotyczy ciał, które poruszają się przy niskich prędkościach płynów z reżimem laminarnym.

W drugim modelu, znanym jako Opór kwadratowy O prawa Rayleight, wielkość siły tarcia jest obliczana zgodnie z:

F_dotykać = ½ ρ.DO.C_D.v²

Gdzie ρ jest gęstością płynu, a jest obszarem krzyżowym obiektu i c_D Jest to aerodynamiczny współczynnik oporności.

Produkt ½ ρ.DO.C_D  Jest to ciągła aerodynamika zwana D, której jednostkami są kg/m, dlatego:

F_dotykać = DV²

Ten model jest bardziej odpowiedni, gdy prędkość obiektów jest średnia lub wysoka, ponieważ ruch wytwarza turbulencje lub wiruje na swojej ścieżce w płynie.

Poruszająca się piłka tenisowa i samochody na autostradzie to przykłady obiektów, w których ten model działa całkiem dobrze.

Siła wiskozowa powstaje, ponieważ ciało stałe musi przyjmować warstwy płynów, aby móc się przez nią poruszać. Istnienie kilku modeli wynika z tego, że siła ta zależy od wielu czynników, takich jak lepkość płynu, prędkość i kształt obiektu.

Może ci służyć: jaka jest względna przepuszczalność?

Istnieje więcej obiektów aerodynamicznych niż inne, a wiele z nich jest dokładnie zaprojektowanych, aby opór środka zmniejszył jego prędkość do minimum.

[TOC]

Przykłady tarcia wiskozowego

Każda osoba lub przedmiot, który porusza się w płynie, koniecznie doświadcza oporu ze strony środowiska, ale wiele razy te efekty są pogardzane za proste zastosowania, takie jak wolny upadek.

W oświadczeniach prawie wszystkich problemów z wolnym upadkiem zauważa się, że skutki oporu powietrza gardzą się. Dzieje się tak, ponieważ powietrze jest raczej „cienkim” płynem i dlatego mamy nadzieję, że tarcie, które oferuje nie znaczące.

Ale istnieją inne ruchy, w których lepkie tarcie ma bardziej decydujący wpływ, zobaczmy kilka przykładów:

Kamienie, które wpadają w ziarenę wody i pyłku

-Skała, która wpada pionowo do rurki pełnej oleju, doświadcza siły, która sprzeciwia się jej zejściu, dzięki odporności na płyn.

-Ziarna pyłku są bardzo małe, więc dla nich odporność powietrza nie jest nieistotna, ponieważ dzięki tej sile udaje się pozostać na powierzchni przez długi czas, powodując sezonowe alergie.

Rysunek 2. Ziarna pyłku są wystarczająco małe, aby odporność na powietrze miała znaczący efekt. Źródło: Pikrepo.

Pływacy i rowerzyści

-W przypadku pływaków używają kapelusza i ogolą się całkowicie, aby odporność wody nie odejmowała prędkości.

-Podobnie jak pływacy, rowerzyści w kontrreloJ doświadczają odporności na powietrze, w konsekwencji hełmy mają projekty aerodynamiczne w celu poprawy wydajności.

Również pozycja rowerzysty w grupie w konkurencji jest istotna. Ten, który kieruje marszem, najwyraźniej otrzymuje największy opór powietrza, podczas gdy dla tych, którzy zamykają marsz, jest to prawie zerowe.

Może ci służyć: Druga równowaga Warunek: wyjaśnienie, przykłady, ćwiczenia

Paracharidystów

-Po otwarciu spadochronu, jest on narażony na lepkie tarcie powietrza, będąc najbardziej odpowiednim modelem, który ma kwadrat prędkości. W ten sposób zmniejsza swoją prędkość, a w miarę upadku pocierania się osiąga stałą wartość graniczną.

Samochody

-W przypadku samochodów współczynnik oporności aerodynamicznej, stała, która jest określona eksperymentalnie i powierzchnia, którą przedstawia przeciwko wiatrowi, są czynnikami decydującymi o zmniejszeniu odporności na powietrze i zmniejszenia zużycia zużycia. Dlatego są one zaprojektowane z nachylonymi szybami.

Eksperyment z kroplami oleju Millikan

-W eksperymencie z kropli olejowej Millikan fizyk Robert Millikan zbadał ruch kropli oleju na środku jednolitego pola elektrycznego, stwierdzając, że dowolny ładunek elektryczny jest wielokrotnym obciążenia elektronem.

W tym celu konieczne było znanie promienia kropli, którego nie można było określić za pomocą bezpośredniej miary, biorąc pod uwagę jego niewielki rozmiar. Ale w tym przypadku lepkie tarcia było znaczące, a krople zakończyły się hamowaniem. Fakt ten pozwolił na określenie promienia kropli, a następnie jego ładunek elektryczny.

Ćwiczenia

- Ćwiczenie 1

W równaniu lepkiej siły tarcia z niską prędkością:

F_dotykać = ΓV

a) Jakie wymiary powinien mieć lepki współczynnik tarcia γ?

b) Jakie są jednostki γ w międzynarodowym systemie jednostek?

Rozwiązanie

W przeciwieństwie do statycznych lub kinetycznych współczynników tarcia, lepki współczynnik tarcia ma wymiary, które muszą być:

Może ci służyć: adhezja fizyczna: co to jest i przykłady

Siła / prędkość

Siła ma wymiary masy x długość /czas², podczas gdy prędkości są długość/czas. Oznaczając je w następujący sposób:

-Masa: m

-Długość: l

-Czas: t

Wymiary lepkiego współczynnika tarcia γ to:

[M.L /t²] / [L / t] = [m.L.T / l.T²] = M/t

Rozwiązanie b

W SI jednostki γ to kg/s

- Ćwiczenie 2

Biorąc pod uwagę odporność, że woda się sprzeciwia, znajdując wyrażenie prędkości końcowej metalowej sferki, która w przypadkach upada pionowo do rurki pełnej oleju:

a) Niska prędkość

b) duża prędkość

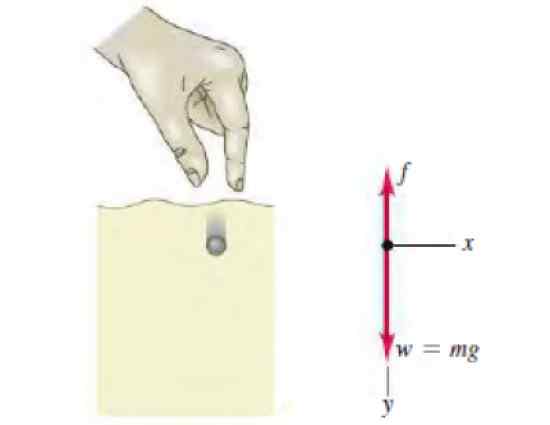Rysunek 3. Schemat wolnego ciała sfertu, który schodzi w płynie. Źródło: Sears, Z. Fizyka uniwersytecka z nowoczesną fizyką.

Rozwiązanie

Na rysunku pojawia się schemat wolnego ciała, pokazujący dwie siły, które działają na sferytu: ciężar w dół i odporność płynu, proporcjonalna do prędkości, w górę. Drugie prawo Newtona dla tego ruchu określa:

γV_T - mg = 0

Gdzie v_T Jest to prędkość końcowa, podana przez:

v_T = mg / γ

Rozwiązanie b

Jeśli przypuszczamy, że średnia przy dużych prędkościach, odpowiednim modelem jest ten z prędkością kwadratową:

F_dotykać = ½ ρ.DO.C_D.v²

Więc:

½ ρ.DO.C_D.v² - mg = 0

D.v² - mg = 0

v = √ [mg / d]

W obu sytuacjach, im większa masa obiektu, tym większa jest jego prędkość końcowa.

Bibliografia

1. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.
2. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.
3. Tipler, str. (2006) Physics for Science and Technology. Ed. Tom 1. Redakcja Reverted.
4. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. McGraw Hill
5. Uniwersytet Sevilla. Siły tarcia. Odzyskany z: Laplace.nas.Jest.