Wspólny czynnik grupowania warunków, ćwiczenia

On Wspólny czynnik grupowania warunków Jest to procedura algebraiczna, która umożliwia pisanie niektórych wyrażeń algebraicznych w postaci czynników. Aby osiągnąć ten cel, wyrażenie musi najpierw wygodnie grupować i obserwować, że każda w ten sposób utworzona grupa ma w efekcie wspólny czynnik.

Prawidłowe zastosowanie techniki wymaga pewnej praktyki, ale w krótkim czasie można zdominować. Spójrzmy najpierw ilustrujący przykład opisany krok po kroku. Następnie czytelnik może zastosować to, czego się nauczył w każdym z ćwiczeń, które pojawią się później.

Rysunek 1. Usuń wspólny czynnik grupowania terminów ułatwia pracę z wyrażeniami algebraicznymi. Źródło: Pixabay.

Załóżmy na przykład, że musisz uwzględnić następujące wyrażenie:

2x² + 2xy - 3zx - 3zy

Ta ekspresja algebraiczna składa się z 4 monomialnych lub terminów, oddzielonych znakami + i -, a mianowicie:

2x², 2xy, -3zx, -3zy

Obserwując ostrożnie, X jest wspólne dla pierwszych trzech, ale nie ostatniego, podczas gdy i jest wspólny dla drugiego i czwartego, a Z jest wspólny dla trzeciego i czwartego.

Zasadniczo nie ma wspólnego czynnika dla czterech terminów jednocześnie, ale jeśli są one zgrupowane, ponieważ zostaną wyświetlone w poniższej sekcji, można pomóc napisać wyrażenie jako iloczyn dwóch lub więcej czynników.

[TOC]

Przykłady

Uwzględnić wyrażenie: 2x² + 2xy - 3zx - 3zy

Krok 1: Grupa

2x² + 2xy - 3zx - 3zy = (2x² + 2xy) + (-3zx - 3zy)

Krok 2: Usuń wspólny współczynnik z każdej grupy

2x² + 2xy - 3zx - 3zy =

= (2x² + 2xy) - (3zx + 3zy) =

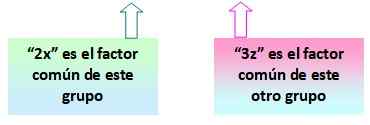
= 2x (x+y) - 3z (x+y)

SiemaMportante: Znak ujemny jest również wspólnym czynnikiem, który należy wziąć pod uwagę.

Może ci służyć: przestrzeń wektorowa: podstawa i wymiar, aksjomaty, właściwości

Teraz zauważ, że nawias (x+y) jest powtarzany w dwóch terminach uzyskanych podczas grupowania. To jest wspólny czynnik, którego szukał.

Krok 3: Faktorizuj wszystkie wyrażenie

2x² + 2xy - 3zx - 3zy = (x+y) (2x - 3z)

Wraz z poprzednim wynikiem osiągnięto cel faktoryzacji, co jest niczym innym jak przekształceniem wyrażenia algebraicznego opartego na sumach i odejmowaniu terminów, w ilocie dwóch lub więcej czynników, w naszym przykładzie: (x+ y) i (2x - 3z).

Ważne kwestie dotyczące wspólnego czynnika grupowego

Pytanie 1: Jak wiedzieć, że wynik jest prawidłowy?

Odpowiedź: Własność dystrybucyjna jest stosowana do uzyskanego wyniku, a po zmniejszeniu i uproszczeniu wyrażenie osiągnięte w ten sposób musi pokryć się z oryginałem, jeśli nie, wystąpił błąd.

W poprzednim przykładzie działa odwrotnie z wynikiem, aby sprawdzić, czy jest w porządku:

(x+y) (2x - 3z) = 2x² -3ZX +2xy - 3zy

Ponieważ kolejność dodatków nie zmienia sumy, po zastosowaniu właściwości dystrybucyjnej, wszystkie oryginalne warunki, zawierają objawy, dlatego faktoryzacja jest poprawna.

Pytanie 2: Czy mógłbyś pogrupować w inny sposób?

Odpowiedź: Istnieją wyrażenia algebraiczne, które przyznają więcej niż jedną formę grupowania i inne, które tego nie robią. W wybranym przykładzie czytelnik może wypróbować inne możliwości, na przykład grupowanie:

2x² + 2xy - 3zx - 3zy = (2x²- 3ZX) + (2xy - 3zy)

I widać, że wynik jest taki sam, jak tutaj uzyskany. Znalezienie optymalnej grupy to kwestia praktyki.

Może ci służyć: Cotangent Donived: obliczanie, demonstracja, ćwiczenia

Pytanie 3: Dlaczego konieczne jest uzyskanie wspólnego czynnika z wyrażenia algebraicznego?

Odpowiedź: Ponieważ istnieją zastosowania, w których czynnikowe wyrażenie ułatwia obliczenia. Załóżmy na przykład, że chcesz zrobić 2x² + 2xy - 3zx - 3zy równy 0. Jakie byłyby możliwości?

Aby odpowiedzieć na ten problem, wersja faktoryzowana jest znacznie bardziej przydatna niż oryginalny rozwój pod względem. Występuje tak:

(x+y) (2x - 3z) = 0

Jedną z możliwości, że wyrażenie jest warte 0, jest to, że x = -y, niezależnie od wartości z. A drugim jest to, że x = (3/2) z, bez znaczenia wartości y.

Ćwiczenia

- Ćwiczenie 1

Uzyskaj wspólny czynnik następującego wyrażenia poprzez grupowanie terminów:

ax+ay+bx+przez

Rozwiązanie

Pierwsze dwa są pogrupowane, z wspólnym czynnikiem „A” i dwoma ostatnimi z wspólnym czynnikiem „B”:

ax+ay+bx+by = a (x+y)+b (x+y)

Po zakończeniu ujawniono nowy wspólny czynnik, który jest (x+y), aby:

ax+ay+bx+by = a (x+y)+b (x+y) = (x+y) (a+b)

Inny sposób na grupowanie

To wyrażenie przyznaje inny sposób grupowania. Zobaczmy, co się stanie, jeśli terminy zostaną poddane i wykonane jest grupa, z którą zawierają X i inna z tymi, które zawierają i:

ax +ay +bx +przez = ax +bx +ay +by = x (a +b) +y (a +b)

W ten sposób nowym wspólnym czynnikiem jest (A+B):

ax+ay+bx+przez = ax+bx+ay+by = x (a+b)+y (a+b) = (x+y) (a+b)

To prowadzi do tego samego wyniku pierwszego sposobu grupowania, który został przetestowany.

- Ćwiczenie 2

Wymagane jest napisanie następującego wyrażenia algebraicznego, ponieważ dwa czynniki produktu:

3³ - 3²B+9AB²-Do²+AB-3B²

Może ci służyć: Koplanares Punkty: Równanie, przykład i rozwiązane ćwiczenia

Rozwiązanie

To wyrażenie zawiera 6 terminów. Spróbujmy grupować pierwszy i czwarty, drugi i trzeci, a na koniec piąty i szósty:

3³ - 3²B+9AB²-Do²+AB-3B² = (3³ -Do²) + (- 3²B+9AB²) + (AB-3B²)

Teraz każdy nawias jest czynnikiem:

= (3³ -Do²) + (- 3²B+9AB²) + (Ab -3b²) = a² (3a -1) + 3AB (3b -a) + B (a -3b)

Na pierwszy rzut oka wydaje się, że sytuacja była skomplikowana, ale czytelnikowi nie należy zniechęcić, ponieważ zamierzamy przepisać ostatni termin:

Do² (3a -1) + 3ab (3b -a) + b (a -3b) = a² (3a - 1) + 3ab (3b -a) - b (3b -a)

Ostatnie dwa terminy mają teraz wspólny czynnik, który jest (3b-A), więc można je rozmiarkować. Bardzo ważne jest, aby nie stracić z oczu pierwszego terminu² (3a - 1), który musi nadal towarzyszyć wszystkim jako dodanie, więc nie pracujesz z nim:

Do² (3a - 1) + 3ab (3b -a) - b (3b -a) = a² (3a-1) + (3b-a) (3AB-B)

Wyrażenie zostało zredukowane do dwóch terminów, a nowy wspólny czynnik został odkryty w ostatnim, czyli „B”. Teraz pozostaje:

Do² (3a-1) + (3b-a) (3AB-B) = a² (3a-1) +B (3b-A) (3a-1)

Kolejnym wspólnym czynnikiem występującym jest 3–1: 1:

Do² (3a - 1) +B (3b -a) (3a -1) = (3a - 1) [a² + B (3B-A)]

Lub jeśli wolisz bez kwadratowych nawiasów:

(3 - 1) [a² + B (3b -a)] = (3a - 1) (a² -AB + 3B²)

Czy czytelnik może znaleźć inny sposób grupowania, który prowadzi do tego samego wyniku?

Rysunek 2. Proponowane ćwiczenia czynnikowe. Źródło: f. Zapata.

Bibliografia

1. Baldor, a. 1974. Algebra podstawowa. Wenezuelski kulturalny s.DO.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Główne przypadki faktoryzacji. Odzyskany z: Julioprofe.internet.
4. Unam. Podstawowa matematyka: czynnikowanie poprzez grupowanie warunków. Wydział rachunkowości i administracji.
5. Zill, d. 1984. Algebra i trygonometria. MacGraw Hill.