Przestrzeń wektora bazowego i wymiaru, aksjomaty, właściwości

A Przestrzeń wektorowa To jest nieopustowany zestaw V= Lub, v, W,…, którego elementy są wektorami. Wraz z nimi przeprowadzane są ważne operacje, wśród których wyróżniają się następujące:

- Suma między dwoma wektorami u + v w rezultacie z, który należy do całości V.

- Mnożenie liczby rzeczywistej α przez wektor v: α v To daje inny wektor I który należy do V.

Artystyczna wizja przestrzeni wektorowej. Źródło: Pixabay

Aby oznaczyć wektor, używamy Bold (v Jest wektorem), a dla skalariuszy lub liczb greckich (α to liczba).

[TOC]

Aksjomaty i właściwości

Aby być przestrzenią wektorową, kolejne osiem aksjomatów musi zostać spełnione:

1-konstrukcyjny: Lub +v = v +Lub

2-Transitivity: (Lub + v) + W = Lub + ( v + W)

3-istnienie wektora zerowego 0 tak, że 0 + v = v

4-istnienie przeciwnego: przeciwieństwo v Jest (-v) , jeśli się uwzględni v + (-v) = 0

Dystrybucja 5 produktów w odniesieniu do sumy wektora: α ( Lub + v ) = αLub +αv

Dystrybucja 6 produktów w odniesieniu do sumy skalarnej: (α + β)v = αv +βv

7-asocjacyjność produktu skalarnego: α (β v) = (α β)v

8-liczba 1 Jest to neutralny element od: 1v = v

Przykłady przestrzeni wektorowych

Przykład 1

Wektory w płaszczyźnie (R²) są przykładem przestrzeni wektorowej. Wektor w płaszczyźnie jest obiektem geometrycznym, który ma wielkość i kierunek. Jest reprezentowany przez zorientowany segment, który należy do wspomnianej płaszczyzny i o wielkości proporcjonalnym do jego wielkości.

Suma dwóch wektorów w płaszczyźnie można zdefiniować jako operację geometryczną drugiego wektora po pierwszym. Rezultatem suma jest zorientowany segment, który zaczyna się od pochodzenia pierwszego i dociera do końca drugiego.

Na rysunku można zauważyć, że suma w R² jest przemienna.

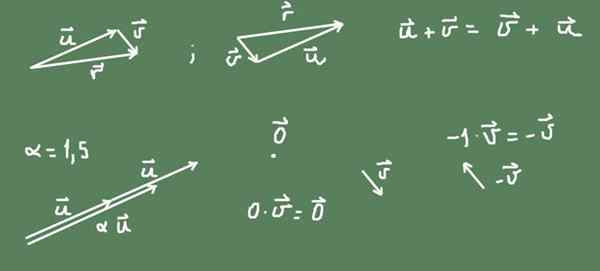Rysunek 2. Wektory w płaszczyźnie tworzą przestrzeń wektorową. Źródło: Self Made.

Produkt liczby α jest również zdefiniowany przez wektor. Jeśli liczba jest dodatnia, oryginalny adres wektorowy jest utrzymywany, a rozmiar jest α razy większy niż oryginalny wektor. Jeśli liczba jest ujemna, adres jest odwrotny, a wynikowy rozmiar wektora jest wartością bezwzględną liczby.

Wektor przeciwny wektora v Jest -v = (-1) v.

Wektor zerowy jest punktem w płaszczyźnie R², a liczba zerowa przez wektor powoduje wektor zerowy.

Wszystkie powiedziane jest ilustrowane na rycinie 2.

Przykład 2

Ustawić P Spośród wszystkich wielomianów mniejszych lub równych dwóch, w tym klasy zerowej, tworzą zestaw, który spełnia wszystkie aksjomaty przestrzeni wektorowej.

Może ci służyć: wzajemnie wykluczające się wydarzenia: właściwości i przykłady

Być wielomianowym p (x) = a x² + b x + c y q (x) = d x² + e x + f

Suma dwóch wielomianów jest zdefiniowana: p (x) + q (x) = (a + d) x² + (b + e) ​​x + (c + f)

Suma wielomianów należących do całości P Jest ono przemienne i przechodnie.

Zerowy wielomian należący do całości P Jest to taki, który ma wszystkie swoje współczynniki równe zero:

0 (x) = 0 x² + 0 x + 0

Suma skalara α jest definiowana przez wielomian, taki jak: α p (x) = α ∙ a x² + α ∙ b x + α ∙ c

Przeciwny wielomian p (x) to -p (x) = (-1) p (x).

Z wszystkich powyższych wynika, że ​​zestaw P Spośród wszystkich wielomianów mniejszych lub równych dwóch, jest to przestrzeń wektorowa.

Przykład 3

Ustawić M spośród wszystkich macierzy m wierszy x n kolumn, których elementy są liczbami rzeczywistymi tworzą rzeczywistą przestrzeń wektorową, w odniesieniu do suma macierzy i produktu liczby według macierzy.

Przykład 4

Zestaw F ciągłych funkcji zmiennej rzeczywistej, tworzą przestrzeń wektorową, ponieważ suma dwóch funkcji można zdefiniować, pomnożenie skalaru przez funkcję, funkcję zerową i funkcję symetryczną. Wypełniają również aksjomaty, które charakteryzują przestrzeń wektorową.

Podstawa i wymiar przestrzeni wektorowej

Baza

Zestaw liniowo niezależnych wektorów jest definiowany jako podstawa przestrzeni wektorowej, tak że z ich liniowej kombinacji można wygenerować dowolny wektor tego wektora.

Liniowo łączenie dwóch lub więcej wektorów polega na pomnożaniu wektorów przez jakiś skalar, a następnie dodawanie ich wektorowo.

Na przykład w przestrzeni wektorowej wektora w trzech wymiarach utworzonych przez R³ zasady kanoniczne zdefiniowane przez wektory jednostkowe (wielkości 1) stosuje się (wielkości 1) Siema, J, k.

Gdzie Siema = (1, 0, 0); J = (0, 1, 0); k = (0, 0, 1). Są to wektory kartezjańskie lub kanoniczne.

Dowolny wektor V należący do R³ jest napisane jako V = a Siema + B J + C k, który jest liniową kombinacją wektorów podstawowych Siema, J, k. Skalary lub liczby a, b, c są znane jako komponenty kartezjańskie V.

Mówi się również, że wektory podstawowe przestrzeni wektorowej tworzą zestaw przestrzeni wektorowej.

Wymiar

Wymiar przestrzeni wektorowej to kardynalna liczba podstaw wektorowej dla wspomnianej przestrzeni; to znaczy liczba wektorów, które składają się na wspomnianą bazę.

Ten kardynał to maksymalna liczba liniowo niezależnych wektorów tej przestrzeni wektorowej, a jednocześnie minimalna liczba wektorów, które tworzą generujący zestaw wspomnianej przestrzeni.

Może ci służyć: populacja statystyczna: koncepcja, typy, przykłady

Podstawy przestrzeni wektorowej nie są unikalne, ale wszystkie podstawy tej samej przestrzeni wektorowej mają ten sam wymiar.

Podprzestura wektorowa

Podstawa wektorowa przestrzeni wektorowej V to podzbiór V, w którym te same operacje są zdefiniowane jako w V i spełnia wszystkie aksjomaty przestrzeni wektorowej. Dlatego podprzedaż będzie również przestrzenią wektorową.

Przykładem podprzestrzeni wektorowej są wektory należące do płaszczyzny XY. Ta podprzestrzeń jest podzbiorem przestrzeni wektorowej wymiarowości większej niż zbiór wektorów należących do trójwymiarowej przestrzeni XYZ.

Innym przykładem podprzestrzeni wektorowej S1 przestrzeni wektorowej jest wszystkie macierze 2 × 2 z elementami rzeczywistymi, jest ten zdefiniowany poniżej:

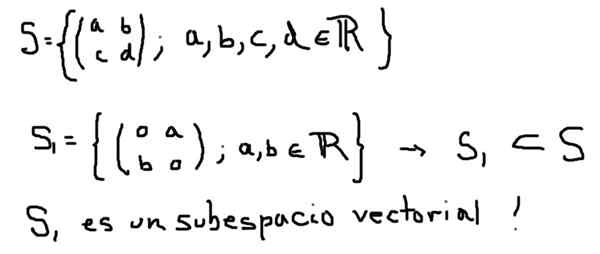
Z drugiej strony S2 zdefiniowane poniżej, chociaż jest to podzbiór S, nie tworzy podprzestrzeni wektorowej:

Rozwiązane ćwiczenia

-Ćwiczenie 1

Być wektorami V1= (1, 1, 0); V2= (0, 2, 1) i V3= (0, 0, 3) w R³.

a) udowodnić, że są one niezależne liniowo.

b) Udowodnij, że tworzą podstawę w R³, ponieważ dowolna lista (x, y, z) można zapisać jako liniową kombinację v1, v2, v3.

c) Znajdź elementy listy V = (-3,5,4) u podstawy V1, V2, V3.

Rozwiązanie

Kryterium wykazania niezależności liniowej jest ustalenie następującego zestawu równań w α, β i γ

α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

W przypadku, gdy jedynym rozwiązaniem tego układu jest α = β = γ = 0, wektory są liniowo niezależne, w przeciwnym razie nie są one.

Aby osiągnąć wartości α, β i γ, proponujemy następujący układ równań:

α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0

α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0

α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0

Pierwszy prowadzi do α = 0, drugiego α = -2 ∙ β, ale jako α = 0, a następnie β = 0. Trzecie równanie oznacza, że ​​γ = (-1/3) β, ale jako β = 0, a następnie γ = 0.

Odpowiedz

Stwierdzono, że jest to zestaw liniowo niezależnych wektorów w R³ .

Odpowiedź b

Teraz napiszmy listę (x, y, z) jako liniową kombinację v1, v2, v3.

(x, y, z) = α v1 + β v2 + γ v3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + β ∙ 2 + γ ∙ 0 = y

Może ci służyć: Turs Tukey: Co to jest w przypadku przykładu rozwiązanego ćwiczenia

α ∙ 0 + β ∙ 1 + γ ∙ 3 = z

Gdzie masz:

α = x

α + 2 β = y

β + 3 γ = z

Pierwszy wskazuje α = x, drugi β = (y-x)/2 i trzeci γ = (z-y/2 +x/2)/3. W ten sposób znaleźliśmy generatory α, β i γ dowolnej listy R³ 

Odpowiedź c

Znajdźmy elementy listy V = (-3,5,4) u podstawy V1, V2, V3.

Zastępujemy odpowiednie wartości w wyrażeniach znalezionych powyżej dla generatorów.

W tym przypadku mamy: α = -3; β = (5-(-3))/2 = 4; γ = (4- 5/2 +(- 3)/2)/3 = 0

To jest:

(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)

Wreszcie:

V = -3 V1 + 4 V2 + 0 V3

Stwierdzamy to V1, v2, v3 Tworzą podstawę w przestrzeni wektorowej R3 o wymiarach 3.

-Ćwiczenie 2

Ekspresowy wielomian p (t) = t² + 4t -3 jako liniowa kombinacja p1 (t) = t² -2t + 5, p2 (t) = 2T² -3T i p3 (t) = t + 3.

Rozwiązanie

P (t) = x p1 (t) + i p2 (t) + z p3 (t)

gdzie należy określić liczby x, y, z.

Poprzez mnożenie i grupowanie warunków z tym samym stopniem w T jest uzyskiwane:

T² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)

Co prowadzi nas do następującego systemu równań:

x + 2y = 1

-2x -3y + z = 4

5x + 3z = -3

Rozwiązania tego układu równań to:

x = -3, y = 2, z = 4.

To jest:

P (t) = -3 p1 (t) + 2 p2 (t) + 4 p3 (t)

-Ćwiczenie 3

Pokaż wektory V1= (1, 0, -1, 2); V2= (1, 1, 0, 1) i V3= (2, 1, -1, 1) R⁴ są liniowo niezależne.

Rozwiązanie

Liniowo łączymy trzy wektory V1, V2, V3 I domagamy się, aby kombinacja dodała element zerowy R⁴

Do V1 + B V2 + C V3 = 0

To jest do powiedzenia,

A (1, 0, -1, 2) + B (1, 1, 0, 1) + C (2, 1, -1, 1) = (0, 0, 0, 0)

To prowadzi nas do następującego systemu równań:

A + B + 2 C = 0

B + C = 0

-A - c = 0

2 A + B + C = 0

Odejmując pierwszy i czwarty, mamy: -a + c = 0 Co implikuje a = c.

Ale jeśli spojrzymy na trzecie równanie, musimy = -c. Jedynym sposobem na spełnienie a = c = (-c) jest to, że C wynosi 0, a zatem również wynosi 0.

A = c = 0

Jeśli zastąpimy ten wynik w pierwszym równaniu, stwierdzamy, że B = 0.

Wreszcie a = b = c = 0, więc można stwierdzić, że wektory v1, v2 i v3 są liniowo niezależne.

Bibliografia

1. Lipschutz, s. 1993. Algebra liniowa. Druga edycja. McGraw - Hill. 167 - 198.