Normalny wysiłek, z którego składa się, jak jest obliczane, przykłady

On normalny wysiłek Zastosowane do określonego materiału, zwanego również wysiłkiem jednoosiowym, jest to związek między przyłożoną siłą prostopadłą do określonej powierzchni a obszarem krzyżowym, na którym działa, lub obciążenie na jednostkę obszaru. Matematycznie, jeśli p jest wielkością siły, a a jest obszarem, w którym jest stosowana, wysiłek σ jest ilorazem: σ = p/a.

Jednostki normalnego wysiłku w systemie międzynarodowym to Newton /Metro², znany jako Pascal i skrócony PA. To są te same jednostki ciśnieniowe. Inne jednostki pojawiające się w literaturze to często funty / cal² albo psi.

Rysunek 1. Skały są stale narażone na wysiłki z powodu aktywności tektonicznej, powodując deformacje w skorupie Ziemi. Źródło: Pixabay.

Na rycinie 2 2 siły o równej wielkości są stosowane prostopadle do obszaru krzyżowego, co powoduje przyczepność na samym pasku, która ma tendencję do rozszerzenia.

Siły te wykonują normalny wysiłek, który nazywa się również Obciążenie osiowe wyśrodkowany, ponieważ jego linia działania pokrywa się z osi osiowej, na której znajduje się centroid.

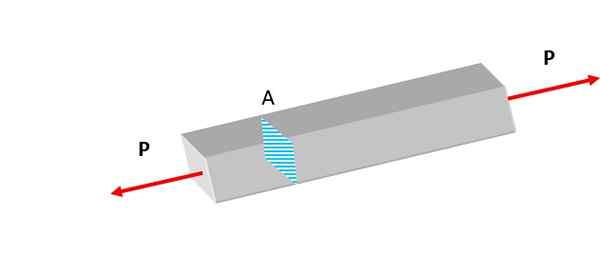Rysunek 2. Pokazany pasek podlega siłom trakcyjnym. Źródło: Self Made.

Wysiłki, czy to normalne, czy inne typy, pojawiają się w naturze w sposób ciągły. W litosferze skały podlegają grawitacji i aktywności tektonicznej, eksperymentując deformacje.

W ten sposób powstają konstrukcje, takie jak fałdy i awarie, których badanie jest ważne w użyciu minerałów i inżynierii lądowej, dla budowy budynków i dróg, aby wymienić kilka przykładów.

[TOC]

Jak to jest obliczane?

Równanie podane na początku σ = P/A pozwala na obliczenie średniego normalnego wysiłku na danym obszarze. Wartość P jest wielkością powstałej siły na obszarze przyłożonym do środka ciężkości i jest wystarczająca do wielu prostych sytuacji.

W tym przypadku rozkład sił jest jednolity, szczególnie w punktach oddalonych od miejsca, w którym masz poprzeczkę podlegającą przyczepności lub kompresji. Ale jeśli wysiłek jest konieczny do obliczenia w określonym punkcie lub siły nie są równomierne, konieczne jest użycie następującej definicji:

Może ci służyć: zamknięty obwód elektryczny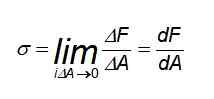

Zasadniczo wartość wysiłku w określonym punkcie może być różna od średniej wartości. W rzeczywistości wysiłek może się różnić w zależności od rozdziału.

Zilustrowano to na poniższym rysunku, na którym siły trakcji F próbują oddzielić pasek w równowadze w sekcjach mm I nn.

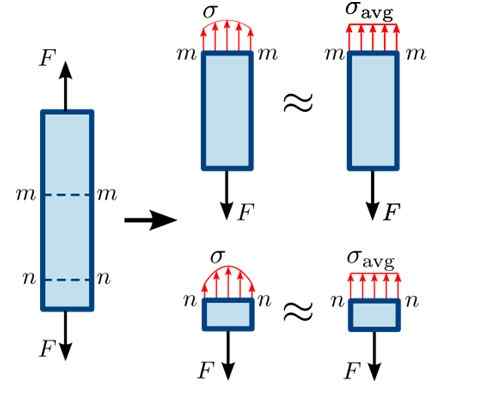Rysunek 3. Rozkład normalnych wysiłków w różnych częściach baru. Źródło: https: // commons.Wikimedia.org/wiki/plik: normal_stress.SVG#/Media/File: Normal_Sress.Svg

Jak sekcja nn Jest bardzo blisko miejsca, w którym siła w dół, rozkład sił na powierzchni nie jest całkowicie jednorodny, a te nieletni są dalej od tego momentu. Dystrybucja jest nieco bardziej jednorodna w sekcji mm.

W każdym razie normalny wysiłek zawsze ma tendencję do rozciągania lub kompresji dwóch części ciała, które znajdują się po obu stronach płaszczyzny, na których działają. Z drugiej strony inne różne wysiłki, takie jak ścinanie, mają tendencję do poruszania się i oddzielania tych części.

Prawo Hooke i normalny wysiłek

Prawo Hooke stwierdza, że ​​w granicach sprężystości normalny wysiłek jest bezpośrednio proporcjonalny do deformacji doświadczonej przez pasek lub przedmiot. W tym wypadku:

Normalny wysiłek ∝ Jednostkowe deformacje

Stała proporcjonalności jest moduł młodego (y):

Normalny wysiłek (σ) = młody moduł (y) x jednolitą odkształcenie (ε)

σ = y. ε

Z ε = δL/L, gdzie ΔL jest różnicą między końcową a początkową długością, czyli l.

Młody moduł lub moduł elastyczności jest charakterystyczną dla materiału, którego wymiary są takie same jak wymiary wysiłku, ponieważ deformacja jednostkowa jest bezwymiarowa.

Może ci służyć: 13 przykładów drugiego prawa Newtona w życiu codziennym

Znaczenie wysiłku w odporności materiałów i geologii

Bardzo ważne jest ustalenie, jak odporne są materiały do ​​wysiłków. Dla konstrukcji stosowanych w budowie budynków, a także w projektowaniu części dla różnych urządzeń, konieczne jest upewnienie się, że wybrane materiały właściwie wypełnią ich funkcję.

Dlatego materiały są wyczerpująco analizowane w laboratoriach poprzez próby, które mają wiedzieć, ile siły mogą się oprzeć przed odkształceniem i zerwaniem, tracąc w ten sposób swoje funkcje. W oparciu o to, decyzja jest podejmowana o tym, czy wyprodukować określony utwór, czy też być częścią urządzenia.

Uważa się, że pierwszym naukowcem, który systematycznie badał oporność materiałów, był Leonardo da Vinci. Zostawił dowody prób, w których ustalił opór przewodów wiszących kamienie różnych pesos.

W wysiłkach zarówno wielkość siły, jak i wymiary struktury, jak i sposób jej zastosowania, jest ważne, aby ustalić granice, w których materiał ma zachowanie elastyczne; to znaczy wraca do swojej pierwotnej formy, gdy wysiłek się ustaje.

W przypadku wyników tych testów przeprowadzane są krzywe deformacji wysiłku dla różnych rodzajów materiałów, takich jak stal, beton, aluminium i wiele innych.

Przykłady

W poniższych przykładach zakłada się, że siły są równomiernie rozmieszczone i że materiał jest jednorodny i izotropowy. Oznacza to, że jego właściwości są takie same w dowolnym kierunku. Dlatego ważne jest zastosowanie równania σ = p/a w celu znalezienia wysiłków.

-Ćwiczenie 1

Na rycinie 3 wiadomo, że średni normalny wysiłek działający w sekcji AB ma wielkość 48 kPa. Znajdź: a) wielkość siły f, która działa w CB, b) wysiłek w sekcji BC.

Może ci służyć: strzelanie poziome: cechy, wzory i równania, ćwiczenia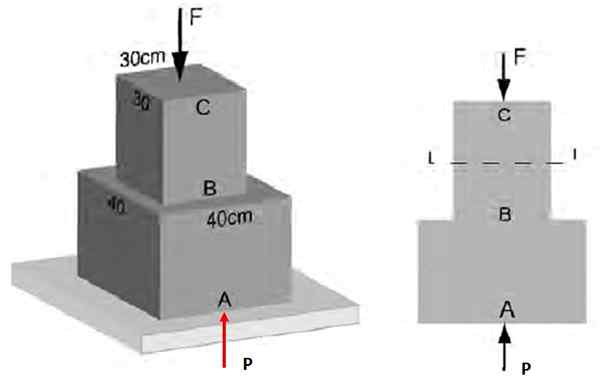Rysunek 4. Normalne wysiłki na temat struktury przykładu 1 ..

Rozwiązanie

Ponieważ struktura jest w równowadze statycznej, zgodnie z drugim prawem Newtona:

P-F = 0

Normalny wysiłek w sekcji AB ma wielkość:

σ_Ab = P/a_Ab

Gdzie p = σ_Ab . DO_Ab = 48000 PA. (40 x 10 ^-2 M)² = 7680 n

Dlatego f = 7680 n

Normalny wysiłek na przekroju BC to stosunek wielkości F a obszarem przekroju po tej stronie:

σ_pne = F/a_pne = 7680 N / (30 x 10 ^-2 M)² = 85.3 kPa.

-Ćwiczenie 2

Drut o długości 150 m i 2.O średnicy 5 mm jest rozciągnięty przez siłę 500 n. Znajdować:

a) wysiłek podłużny σ.

b) Jednolitowe deformacja, wiedząc, że końcowa długość wynosi 150.125 m.

c) moduł elastyczności I tego drutu.

Rozwiązanie

a) σ = f / a = f / π.R²

Promień drutu wynosi połowę średnicy:

R = 1.25 mm = 1.25 x 10^-3 M.

Obszar krzyżowy wynosi π.R², Wtedy wysiłek jest:

σ = f / π.R² = 500 / (π.(1.25 x 10^-3)² PA = 101859.2 pa

b) ε = ΔL / l = (długość końcowa - długość początkowa) / długość początkowa

Dlatego:

ε = (150.125 - 150) /150 = 0.125/150 = 0.000833

c) Moduł Younga drutu jest wyczyszczony poprzez znajomość wartości ε i σ wcześniej obliczonych:

Y = σ / ε = 101859.2 pa / 0.000833 = 1.22 x 10⁸ PA = 122 MPa.

Bibliografia

1. Piwo, f. 2010. Mechanika materiałów. 5. Wydanie. McGraw Hill. 7 - 9.
2. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6^Tth  Wyd. Prentice Hall. 238-242.
3. Hibbeler, R.C. 2006. Mechanika materiałów. 6th. Wydanie. Edukacja Pearsona. 22 -25
4. Valera Negrete, J. 2005. Ogólne uwagi fizyki. Unam. 87-98.
5. Wikipedia. Stres (mechanika). Odzyskane z: Wikipedia.org.