Elipsa

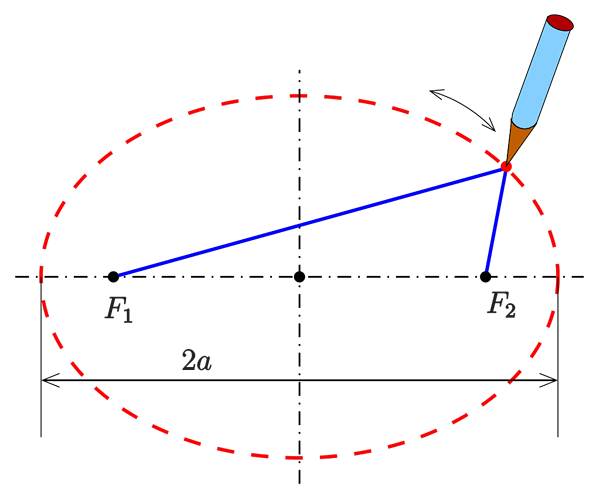
Rysunek 1. Metoda ogrodnika narysowania elipsy. Suma odległości między punktem P elipsy (na czerwono) a reflektorami (w kolorze czarnym) pozostaje stała. Źródło: AG2GAEH, CC BY-SA 4.0, Via Wikimedia Commons.

Co to jest elipsa?

Elipsa to zestaw punktów współrzędnych (x, y), dla których suma odległości do dwóch stałych punktów, nazywana Focos, To jest stałe. Z kolei światła reflektorów są oddzielone od siebie na odległość równą 2c.

Elipsy znajdują się w naturze. Na przykład jest to ruch ziemi wokół Słońca, ponieważ, jak pokazał niemiecki astronom.

Ponadto forma eliptyczna znajduje się w projektowaniu konstrukcji architektonicznych, jest częścią leczenia w celu niszczenia obliczeń nerek i służy kształtowaniu różnorodnych przedmiotów, takich jak czołgi i inne pojemniki.

Na górnej figurze pokazano elipsę z dwoma reflektorami, położonymi w równej odległości od środka figury i na najdłuższej osi. Warunkiem, w którym punkt P musi spełnić, aby należeć do elipsy, jest to, że suma odległości do każdego ostrości jest ustalona:

D₁ + D₂ = stała.

Dlatego, gdy chce ogrodnik. Następnie weź linę dobrej wielkości, zawiąż swoje końce do stawek, a podtrzymanie patyka na linie przesuwa się na nim, aby zaznaczyć eliptyczny rowek na miękkiej Ziemi. To jest Metoda ogrodnika Rysować elipsy.

Elementy Elipse

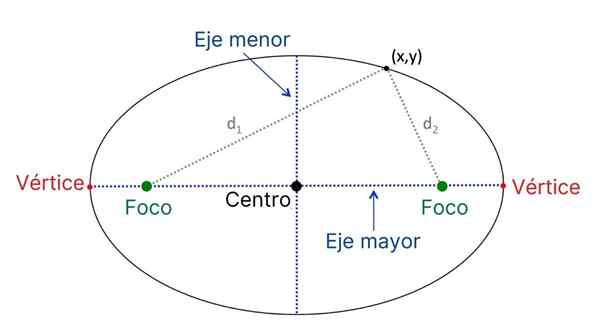Główne elementy elipsy

Są to główne elementy elipsy:

1. Focos, stałe punkty znajdujące się na najdłuższej osi elipsy.
2. Wierzchołki, Są to dwa punkty elipsy, przez które przechodzi linia, która łączy się w centrum uwagi.
3. Główna oś, To lina dołącza do wierzchołków, a także zawiera reflektory.
4. Centrum, Punkt środkowy osi głównej, który odpowiada punkcie współrzędnej (H, K). Każde skupienie jest w równej odległości od środka i na odległość C tego samego.
5. Niewielka oś, To lina przechodzi przez środek i jest prostopadła do głównej osi.
6. Radia wektorowe, segmenty, które łączą każde skupienie z p elipsy.
7. Oś ogniskowa, prosto, na którym są reflektory.
8. Odległość ogniskowa, Jest to odległość między światłami reflektorów, oznaczona jako 2c.
9. Oś wtórna, Oś prostopadła do głównej osi, która jest jednocześnie meditrix tego segmentu, który wiąże się z reflektorami.
10. Centrum symetrii, punkt zbieżny z środkiem elipsy, gdzie skrzyżowane są osie symetrii tego samego.
11. Osie symetrii, linie zawierające największe i mniejsze osie elipsy.

Może ci służyć: opodatkowanie

Rodzaje elipsy

Istnieją dwa rodzaje elipsy:

• Ci, którzy mają główną osi poziomej.
• Ci, którzy mają największą oś pionową.

Następnie są opisane matematycznie:

Elipsa z główną osą poziomą

Niech punkt C współrzędnych (H, K) Środek elipsy, długość osi głównej wynosi 2a, a długość mniejszej osi równa 2b, z A> B.

Równanie tej elipsy jest:

Elipsa z główną osą pionową

Z tymi samymi parametrami elipsy o osi poziomej, elipsa o głównej osi pionowej jest zapisywana jako:

W obu przypadkach odległość od ostrości do centrum C Jest to związane z osadami głównymi i niewielkimi przez:

C² = a² - B²

Przykłady elipsy

Elipsa pozioma

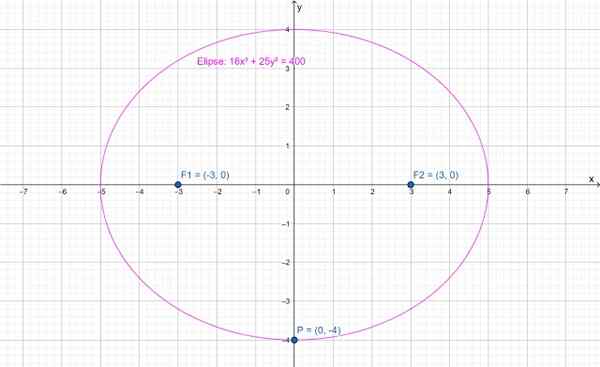
Poniższy obraz pokazuje elipsę, której główna oś jest pozioma. Centrum znajduje się w punkcie (0,0), a reflektors w (-3,0) i (3.0). Podświetlony punkt P (0, -4) należy do elipsy.

Rysunek 2.- Elipsa, której główna oś jest pozioma. Źródło: f. Zapata przez Geogebra.

Równanie tej elipsy jest:

16x² + 25 i² = 400

Nie jest trudno wyrazić to równanie w formie kanonicznej, wystarczy podzielić wszystkie warunki między 400 i uprościć wygodnie (patrz ćwiczenie rozwiązane później).

Elipsa pionowa

Poniżej znajduje się pionowa elipsa, której główna oś pokrywa się z osą i. Koncentruje się na punkcie (0,0), a jego równanie to:

36x² + 9Y² = 324

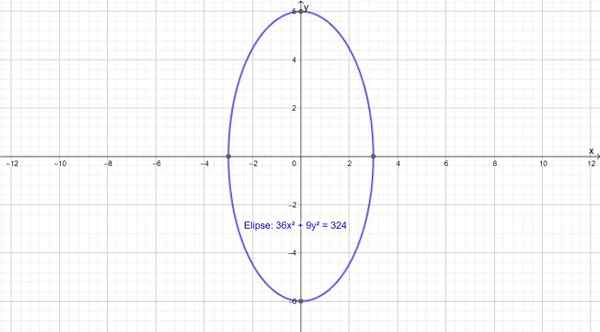Rysunek 3.- Elipsa z główną osą pionową. Źródło: f. Zapata przez Geogebra.

Właściwość refleksji

Składa się z następujących czynności: jeśli odblasek lub źródło dźwięku umieszcza się w jednym z reflektorów elipsy, emitowane fale są odzwierciedlone w kierunku drugiego ostrości. To dobry sposób na przekierowanie fal, w których potrzebna jest Twoja energia.

Może ci służyć: Endecagon

Dlatego w eliptycznych salach, gdy ktoś mówi w jednym z reflektorów, słuchacz zlokalizowany w drugim układzie słucha wyraźnie.

A w medycynie ta właściwość odbicia służy do niszczenia kamieni nerkowych poprzez umieszczenie pacjenta w jednym z reflektorów eliptycznej wanny pełnej wody, podczas gdy generator fali ultradźwiękowej jest umieszczony w drugim ognisku. Fale znajdują odzwierciedlenie w obliczeniach i fragmentują je w mniejszych cząstkach, które są następnie wydalane przez mocz.

Radio Ska

Ten radiowy teleskop jest największy w swoim rodzaju i oczekuje się, że rozpocznie pracę w 2021 roku. Jego powierzchnia to 1 km kwadrat i dlatego nazywa się Ska (w języku angielskim są akronimem Tablica kilometra kwadratowego).

Korzystając z właściwości refleksji elipsów, struktura składa się z układu 3000 anten o eliptycznym kształcie o szerokości około 15 m, rozłożonych między Australią a Afryką Południową. Z tym instrumentem, 50 razy bardziej wrażliwych niż obecnie używane, oczekuje się, że przyjrzy się wszechświatowi, gdy był jeszcze znacznie młodszy: około miliarda lat ledwo.

Rysunek 4.- Artystyczna interpretacja SKA Radio Ska Ska. Źródło: Wikimedia Commons.

Ćwiczenie rozwiązane

Znajdź kanoniczne równania elipsów pokazane na rysunkach 2 i 3, aw każdym przypadku określ długości zmysłów większych i mniejszych, a także odległości ogniskowe.

Rozwiązanie

Dla poziomej elipsy, której równanie to 16x² + 25 i² = 400, wszystkie warunki między 400 są podzielone, co spowodowało:

Może ci służyć: Cotangent Donived: obliczanie, demonstracja, ćwiczenia

 Co jest uproszczone:

Semi -oś „A” mierzy 5 i najmniejsze „B”, które ostrzegają również poprzez uważne obserwowanie obrazu. Jeśli chodzi o odległość ogniskową, musisz:

C² = a² - B²

C² = 25 - 16 = 9 ⇒ C = √9 = 3

Dlatego c = 3 jest odległością między środkiem a jednym z reflektorów. Oba ogniska to odległość 2C = 6.

Co do pionowej elipsy 36x² + 9Y² = 324 masz:

Uproszczenie:

C² = 36 - 9 = 27

C = √27 ≅ 5.2

Dlatego odległość między światłami wynosi 10.4 jednostki.

Bibliografia

1. Hoffman, J. Wybór problemów z matematyką. Tom 3.
2. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
3. Formuły wszechświata. Elipsa. Odzyskane z: Universoformulas.com.
4. Wikipedia. Tablica kilometra kwadratowego. Odzyskane z: jest.Wikipedia.org.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.