Równania wieloparomiczne

Jakie są równania wielomianowe?

Równania wieloparomiczne Są stwierdzeniem, które podnosi równość dwóch wyrażeń lub członków, w których co najmniej jeden z terminów, które składają się na każdą stronę równości, są wielomianami p (x). Równania te są nazwane zgodnie ze stopniem ich zmiennych.

Ogólnie rzecz biorąc, równanie jest stwierdzeniem, które określa równość dwóch wyrażeń, w których co najmniej jeden z nich istnieją nieznane ilości, które nazywane są zmiennymi lub niewiadomymi. Chociaż istnieje wiele rodzajów równań, są one ogólnie podzielone na dwa typy: algebraiczne i transcendentne.

Równania wieloparomiczne zawierają tylko wyrażenia algebraiczne, które mogą mieć jedną lub więcej niewiadomych, które interweniują w równaniu. Zgodnie z wykładnikiem (klasą), które mają, można je sklasyfikować jako: pierwsza klasa (liniowa), druga klasa (kwadratowa), trzecia klasa (sześcienna), czwarta klasa (kwantyczna), stopnia większa lub równa pięć i równa pięć i irracjonalny.

Charakterystyka równań wielomianowych

Równania wieloparomiczne są wyrażeniami, które powstają przez równość między dwoma wielomianami; To znaczy dla skończonych sum mnożenia między wartościami, które są nieznane (zmienne) i liczbami stałymi (współczynniki), gdzie zmienne mogą mieć wykładniki, a ich wartość może być dodatnią liczbą całkowitą, w tym zero.

Wykładniki określają stopień lub rodzaj równania. Ten termin wyrażenia, który ma najbardziej wykładnik wartości, będzie reprezentował bezwzględny stopień wielomianu.

Równania wieloparomiczne są również znane jako algebraiczne, ich współczynniki mogą być liczbami rzeczywistymi lub złożonymi, a zmienne są nieznane liczby reprezentowane przez literę, takie jak: „x”.

Jeżeli zastępując wartość zmienną „x” w p (x), wynik jest równy zero (0), mówi się, że wartość ta spełnia równanie (jest to rozwiązanie) i jest ogólnie nazywana wielomianowym korzeniem korzeniowym.

Kiedy opracowano równanie wielomianowe, wszystkie korzenie lub rozwiązania chcą zostać znalezione.

Rodzaje równań wielomianowych

Istnieje kilka rodzajów równań wielomianowych, które są zróżnicowane w zależności od liczby zmiennych, a także według ich stopnia wykładnika.

Zatem równania wielomianowe -gdzie jego pierwszy termin jest wielomianem, który ma tylko jeden nieznany, biorąc pod uwagę, że jego stopień może być dowolną liczbą naturalną (N), a drugi termin wyraża zero -Kan, w następujący sposób:

Może ci służyć: Historia trygonometrii z jej początków

Do_{N *} X^N + Do_{N-1 *} X^N-1 +… + A_{1 *} X¹ + Do_{0 *} X₀ = 0

Gdzie:

• Do_N, Do_N-1 już₀, Są prawdziwymi współczynnikami (liczbami).
• Do_N różni się od zera.
• Wykładnik N jest dodatnią liczbą całkowitą, która reprezentuje stopień równania.
• x jest zmienną lub nieznaną, której należy szukać.

Absolutny lub większy stopień równania wielomianowego polega na tym, że wykładnik o większej wartości między wszystkimi tymi, którzy tworzą wielomian; W ten sposób równania są klasyfikowane jako:

Pierwsza klasa

Równania wielomianowe pierwszego stopnia, znane również jako równania liniowe, to te, do których stopień (największy wykładnik) jest równy 1, wielomian jest postaci p (x) = 0; I składa się z liniowego i niezależnego terminu. Jest napisane w następujący sposób:

AX + B = 0.

Gdzie:

• A i B są liczbami rzeczywistymi i ≠ 0.
• AX jest terminem liniowym.
• B jest niezależnym terminem.

Na przykład równanie 13x - 18 = 4x.

Aby rozwiązać równania liniowe, wszystkie terminy zawierające nieznane x muszą być przekazywane na bok równości, a te, które nie poruszają się po drugiej stronie, aby je wyczyścić i uzyskać rozwiązanie:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

W ten sposób podane równanie ma tylko jedno rozwiązanie lub korzeń, czyli x = 2.

Druga klasa

Równania wielomianowe drugiego stopnia, znane również jako równania kwadratowe, to te, w których stopień (największy wykładnik) jest równy 2, wielomian jest postaci p (x) = 0 i składa się z kwadratowego terminu, a liniowy i niezależny. Wyraża się to w następujący sposób:

topór² + BX + C = 0.

Gdzie:

• A, B i C są liczbami rzeczywistymi i ≠ 0.
• topór² Jest to termin kwadratowy, a „A” jest współczynnikiem terminu kwadratowego.
• Bx jest terminem liniowym, a „B” jest współczynnikiem terminu liniowego.
• C jest niezależnym terminem.

Rozpuszczalnik

Zasadniczo rozwiązanie tego rodzaju równań jest podawane podczas oczyszczania x równania i pozostaje w następujący sposób, który nazywa się Resourvent:

Może ci służyć: Twierdzenie dwumianowe

Tam (b² - 4AC) nazywa się odróżnieniem od równania, a wyrażenie to określa liczbę roztworów, które może mieć równanie:

• Tak b² - 4ac) = 0, równanie będzie miało jedno rozwiązanie, które jest podwójne; to znaczy, że będzie miał dwa równe rozwiązania.
• Tak b² - 4ac)> 0, równanie będzie miało dwa różne rzeczywiste rozwiązania.
• Tak b² - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

Na przykład masz równanie 4x² + 10x - 6 = 0, aby najpierw go rozwiązać, terminy a, b i c są zidentyfikowane, a następnie są wymieniane w wzorze:

A = 4

B = 10

C = -6.

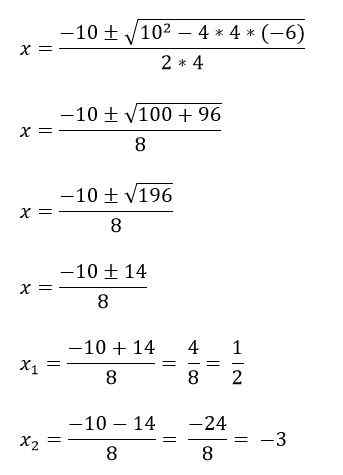
Są przypadki, w których drugie równania wielomianowe drugiego stopnia nie mają trzech terminów i dlatego są one rozwiązywane inaczej:

• W przypadku, że równania kwadratowe nie mają terminu liniowego (to znaczy, B = 0), równanie będzie wyrażone jako ax² + C = 0. Aby to rozwiązać, x jest oczyszczone² A korzenie kwadratowe są stosowane w każdym członku, pamiętając, że dwa możliwe oznaki, które nieznane mogą mieć:

topór² + C = 0.

X² = - c ÷ a

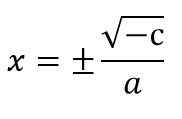
Na przykład 5 x² - 20 = 0.

5 x² = 20

X² = 20 ÷ 5

x = ± √4

x = ± 2

X₁ = 2.

X₂ = -2.

• Gdy równanie kwadratowe nie ma niezależnego terminu (to znaczy, c = 0), równanie będzie wyrażone jako ax² + Bx = 0. Aby to rozwiązać, wspólny czynnik nieznanego X musi być pobrany w pierwszym członku; Ponieważ równanie jest dopasowane do zera, spełnia się, że co najmniej jeden z czynników będzie równy 0:

topór² + Bx = 0.

x (ax + b) = 0.

W ten sposób musisz:

x = 0.

x = -b ÷ a.

Na przykład: masz równanie 5x² + 30x = 0. Najpierw jest to czynnik:

5x² + 30x = 0

x (5x + 30) = 0.

Generowane są dwa czynniki, które są x y (5x + 30). Jeden z nich zostanie uznany za zero, a drugie jest podane rozwiązanie:

X₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

X₂ = -6.

Najwyższa ocena

Główne stopnie równania wielomianowe to te, które obejmują od trzeciej klasy, które można wyrazić lub rozwiązać wraz z ogólnym równaniem wielomianowym dla dowolnego stopnia:

Może ci służyć: współczynnik korelacji: wzory, obliczenia, interpretacja, przykład

Do_{N *} X^N + Do_{N-1 *} X^N-1 +… + A_{1 *} X¹ + Do_{0 *} X₀ = 0

Jest to stosowane, ponieważ równanie o stopniu większym niż dwa jest wynikiem faktoryzacji wielomianu; Oznacza to, że wyraża się to jako pomnożenie wielomianu klasy jednej lub większej, ale bez prawdziwych korzeni.

Rozwiązanie tego rodzaju równań jest bezpośrednie, ponieważ pomnożenie dwóch czynników będzie równe zero, jeśli którykolwiek z czynników jest zerowy (0); Dlatego każde ze stwierdzonych równań wielomianowych musi zostać rozwiązane, dopasowując każdy z jego czynników do zera.

Na przykład masz równanie trzeciego stopnia (sześcienne) x³ + X² +4x + 4 = 0. Aby go rozwiązać, musisz wykonać następujące kroki:

• Warunki są pogrupowane:

X³ + X² +4x + 4 = 0

(X³ + X² ) + (4x + 4) = 0.

• Członkowie rozpadają się, aby uzyskać wspólny czynnik nieznanego:

X² (x + 1) + 4 (x + 1) = 0

(X² + 4)_*(x + 1) = 0.

• W ten sposób uzyskuje się dwa czynniki, które muszą być równe zero:

(X² + 4) = 0

(x + 1) = 0.

• Można zauważyć, że czynnik (x² + 4) = 0 nie będzie miało prawdziwego rozwiązania, podczas gdy współczynnik (x + 1) = 0 Tak. Dlatego rozwiązaniem jest:

(x + 1) = 0

x = -1.

Rozwiązane ćwiczenia

Rozwiąż następujące równania:

Pierwsze ćwiczenie

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Rozwiązanie

W tym przypadku równanie jest wyrażone jako mnożenie wielomianów; to znaczy jest faktoryzowany. Aby go rozwiązać, każdy współczynnik musi być równy zero:

2x² + 5 = 0, nie ma rozwiązania.

x - 3 = 0

x = 3.

1 + x = 0

x = - 1.

W ten sposób podane równanie ma dwa rozwiązania: x = 3 i x = -1.

Drugie ćwiczenie

X⁴ - 36 = 0.

Rozwiązanie

Podano wielomian, który można przypisać jako różnica w kwadratach, aby osiągnąć szybsze rozwiązanie. Zatem równanie pozostaje:

(X² + 6)_*(X² - 6) = 0.

Aby znaleźć rozwiązanie równań, oba czynniki są równe zero:

(X² + 6) = 0, nie ma rozwiązania.

(X² - 6) = 0

X² = 6

x = ± √6.

Zatem początkowe równanie ma dwa rozwiązania:

x = √6.

x = - √6.