Równanie Arrheniusa
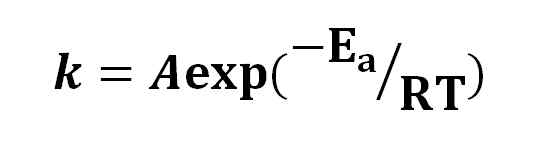
- 3084
- 818
- Estera Wojtkowiak
Jakie jest równanie Arrheniusa?
Równanie Arrheniusa Jest to podejście, które wiąże stałą prędkości reakcji chemicznej w zależności od temperatury. Został założony w 1899 r. Przez szwedzkiego chemika Svante Arrhenius (1859–1927). Reprezentuje jeden z najbardziej fundamentalnych wkładów w rozwój kinetyki chemicznej.
Równanie to zawdzięcza swoje teoretyczne bazy wielu naukowcom, w tym Wihelmy (1850), Berthelot (1862) i J. J. Hood (1885). Ale największy wpływ przypisuje się stworzeniu równania Arrheniusa z pracą wykonaną przez Van't Hoof (1884), który ustalił zależność od stałych równowagi reakcji chemicznych z temperaturą.
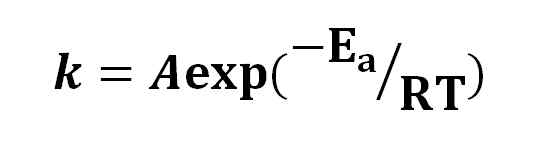 Równanie Arrheniusa. Źródło: Gabriel Bolívar.
Równanie Arrheniusa. Źródło: Gabriel Bolívar. Na podstawie równania Arrheniusa pomysł, że wzrost o 10 ° C spowodował powielanie prędkości reakcji, został rozpowszechniony. Inne interpretacje, które stały się, że cząsteczki potrzebują pewnej energii aktywacji, aby reagować na siebie.
Podobnie wskazuje się, że równanie Arrheniusa jest kolejną formą rozpadu wykładniczego, w którym wartość stałej prędkości w zależności od wykładnika -eDo/Rt, gdzie eDo jest energią aktywacyjną.
Równanie i wyjaśnienie
Równanie Arrhenius ma następujące dwa wyrażenia:
K = ae-EA/RT
Postać równania stosowanego w chemii i jest związana z mole odczynników.
K = ae-EA/KBT
Postać równania stosowanego w fizyce i jest związana z większą liczbą cząsteczek, niż z moli.
Oba pochodzą z równania kopyta Van´ dla zmienności stałej równowagi K, w zależności od temperatury. Podstawowe równanie to:
d (ln k)/dt = eDo/Rt2
Może ci służyć: Dibenzalacetona: właściwości, mechanizm reakcji, zastosowania, ryzykoKtóry jest zintegrowany, zakładając, żeDo jest niezależny od temperatury. Więc mamy:
ln k = - eDo/Rt + ln a
Gdzie ln a jest stałą integracji. Gdy funkcja wykładnicza jest stosowana po obu stronach równania, otrzymujemy już wprowadzone równanie Arrheniusa.
składniki
k
Jest to stała prędkości reakcji chemicznej. Jego wartość można uzyskać, oprócz użycia równania Arrheniusa, poprzez zastosowanie prawa prędkości. Reprezentuje liczbę zderzeń między cząsteczkami wytwarzanymi przez reakcję na sekundę.
DO
Jest to tak zwany czynnik przedefekcjonalny, który reprezentuje częstotliwość zderzeń między cząsteczkami odczynnika z odpowiednią orientacją geometryczną, która może, ale nie musi powodować reakcji chemicznej. Jeśli zmienność temperatury ma niewielką wielkość, zwykle jest traktowana jako stała. Ten czynnik ma swoją własną formułę:
A = z ρ
Gdzie Z jest znany jako współczynnik częstotliwości lub kolizji, oraz ρ współczynnik geometryczny lub steryczny, który wskazuje względną orientację cząsteczek w punkcie kolizji. Stała A ma te same jednostki, co stała prędkości. W przypadku, gdy nie ma energii aktywacji, wielkość A będzie równa wielkości K.
IDo
Jest to energia aktywacji, która reprezentuje energię progową przed osiągnięciem statystyki przejściowej.
Energia aktywacji ma jednostkę KJ/MOL. Ale w obliczeniach J/mol jest używany jako jednostka. Najmniej (-) znak poprzedzający EDo, Służy do wskazania, że jego wzrost powoduje spadek prędkości reakcji, a także spadek prędkości reakcji.
Może ci służyć: chromatografia gazowaRt
Reprezentuje średnią energię kinetyczną. Tymczasem R jest uniwersalną stałą gazów, będąc jedną z jego najczęściej używanych wartości 8.31 J · k-1· Mol-1. A t jest temperaturą bezwzględną wyrażoną w Kelvin (k).
I
Jest to podstawa logarytmów naturalnych lub neperiańskich, mającą wartość 2.71828.
I-EA/RT
Jest to frakcja reagujących cząsteczek o równej lub nadmiernej energii w stosunku do energii aktywacyjnej.
Aplikacje
Większość zastosowań równania Arrhenius pochodzi z użycia w determinowaniu stałej prędkości; a co do końca, prędkość reakcji, a także jej energia aktywacyjna.
Na przykład opracowano model chemiczny w oparciu o równanie Arrheniusa, które może przewidzieć właściwości materiałów jako zmianę ich temperatury, stosowaną w dziedzinach geologii, konstrukcji, inżynierii materiałów oraz w naukach o żywności, a także w dziedzinie nauk o żywności.
Został zastosowany, chociaż z pewną krytyką równanie Arrheniusa w kinetyce reakcji w stanie stałym. Został również wykorzystany do scharakteryzowania odpowiedzi roślin na stres wodny.
Równanie Arerenhius służyło jako podstawa do stworzenia modelu matematycznego, który kwantyfikuje wpływ temperatury na okres użytkowania komórek lub akumulatorów metalowych niklu.
Podobnie, na podstawie równania Arrheniusa, ustalono szybkość rozkładu odpadów świń.
Rozwiązane ćwiczenia
Ćwiczenie 1
Jaka jest energia aktywacji reakcji, jeśli okaże się, że jej prędkość stała potroi się, gdy temperatura wzrośnie z 600 k do 610 K?
Może ci służyć: kwas fenoksyoctowy: synteza, procedura, stosowanie, ryzykoZaczynając od równania Arrheniusa:
k = a · e-EA/RT
Oczyszczamy czynnik A:
A = k1 / (e-EA/RT1)
Ale ponieważ mamy dwie temperatury, t1 oraz T2, Będą dwie stałe prędkości: k1 i k2. Współczynnik A nie zmienia się, więc możemy dopasować go do drugiej temperatury:
k1 / (e-EA/RT1) = k2 / (e-EA/RT2)
I oczyszczanie eDo będziemy mieli:
IDo = R (ln k2/k1) / (1 / t1 - 1/t2)
Jak co2 jest trzy razy większy niż k1,
k2 / k1 = 3
LN (3) = 1.099
A z drugiej strony:
1 / t1 = 1/600 k = 1.66 x 10-3 K-1
1 / t2 = 1/610 k = 1.64 x 10-3 K-1
Zastąpienie wtedy:
IDo = (8.31 J · k-1· Mol-1) (1.099) / (1.66 x 10-3 K-1 - 1.64 x 10-3 K-1)
= 456.5 kJ · mol-1
Ćwiczenie 2
W reakcji fazy gazowej energia aktywacji jest równa 103 kJ/mol, a stała prędkości wynosi 0.085 min-1. Oblicz stałą prędkości przy 323 K.
Z poprzedniego wyrażenia usuwamy LN k2/k1:
ln k2/k1 = (EDo/R) (1 /t1 - 1/t2)
Rozwijanie właściwej części równania:
ln k2/k1 = (103.000 J · mol-1 / 8.31 J · k-1· Mol-1) (1/273 K - 1/323 K)
ln k2/k1 = 6.99
Przyjmowanie antylogarytmów:
k2/k1 = 1.086
k2 = (k1) (1.086)
= (0.085 min-1) (1.086)
= 0.092 min-1
Bibliografia
- Whitten, Davis, Peck i Stanley. (2008). Chemia. (8 wyd.). Cengage Learning.
- Walter J. Moore. (1963). Chemia fizyczna. W kinetyce chemicznej. Czwarta edycja, Longmans.
- Iran. Levine. (2009). Zasady fizykochemii. Szósta edycja. MC Graw Hill.
- Wikipedia. (2020). Równanie Arrheniusa. Źródło: w:.Wikipedia.org
- Guenevieve del Mundo i in. (10 września 2020). Równanie Arrheniusa. Odzyskane z: chem.Librettexts.org
- Clark Jim. (2013). Stałe i równanie Arrheniusa. Odzyskane z: chemguide.współ.Wielka Brytania
- Redaktorzy Enyclopaedia Britannica. (2020). Równanie Arrheniusa. Odzyskane z: Britannica.com
- Helmestine, Anne Marie, pH.D. (28 sierpnia 2020). Wzór równania Arrheniusa i przykład. Odzyskane z: Thoughtco.com

