Domena i sprzeczna funkcja (z przykładami)

Koncepcje domena i sprzeczność funkcji Są one powszechnie nauczane na kursach obliczeniowych nauczanych na początku kariery uniwersyteckiej.

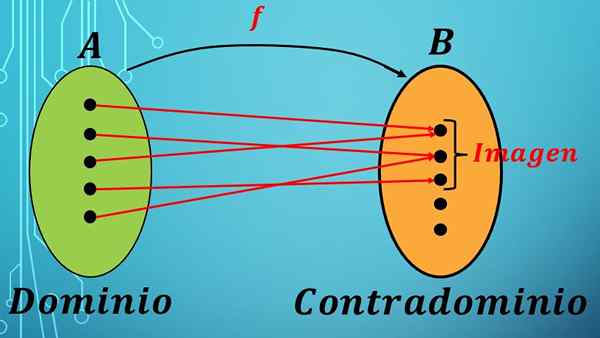
Przed zdefiniowaniem domeny i sprzeczności powinieneś wiedzieć, co to jest funkcja. Funkcja F jest prawem korespondencyjnym (reguła) między elementami dwóch zestawów.

Całość, których wybrane są elementy, nazywa się domeną funkcji, a zestaw, do którego te elementy są wysyłane przez F, nazywane jest sprzeczne.

W matematyce A funkcja z domeną A i sprzecznym B jest oznaczona wyrażeniem F: A → B.

Poprzednie wyrażenie mówi, że elementy zestawu A są wysyłane do zestawu B zgodnie z prawem korespondencyjnym F.

Funkcja przypisuje każdy element zestawu do jednego elementu zestawu B.

Domena i sprzeczność

Biorąc pod uwagę rzeczywistą funkcję rzeczywistej zmiennej f (x), domeną funkcji musi być wszystkie te liczby rzeczywiste, tak że ocena w F, wynik jest liczbą rzeczywistą.

Zasadniczo sprzeczność funkcji jest zbiorem rzeczywistych liczb n. Sprzeczność jest również nazywana zestawem przybycia lub kodominium funkcji f.

Sprzeczność funkcji jest zawsze r?

NIE. Tak długo, jak funkcja nie jest szczegółowo badana, zestaw rzeczywistych liczb jest zwykle traktowany jako sprzeczność.

Ale po zbadaniu funkcji można przyjąć bardziej odpowiedni zestaw jako sprzeczny.

Odpowiedni zestaw wspomniany w poprzednim akapicie zbiega się z obrazem funkcji.

Definicja obrazu lub zakresu funkcji F odnosi się do wszystkich wartości wynikających z oceny elementu domeny w F.

Przykłady domeny i sprzeczności

W poniższych przykładach ilustruje to, jak obliczyć domenę funkcji i jej obrazu.

Przykład 1

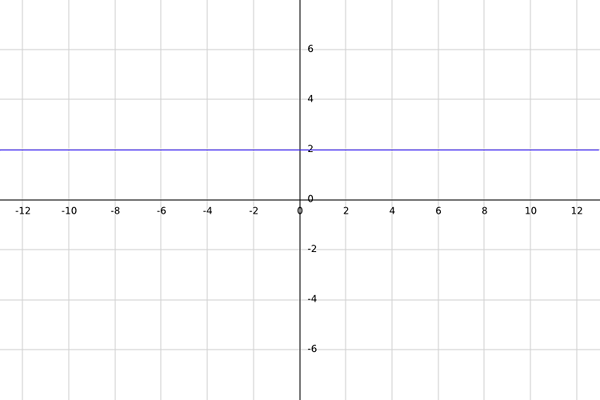
Niech F będzie funkcją rzeczywistą zdefiniowaną przez f (x) = 2.

M -domina F jest liczbami rzeczywistych, tak że podczas oceny ich w F wynik jest liczbą rzeczywistą. Sprzeczność na razie jest równa R.

Ponieważ podana funkcja jest stała (zawsze równa 2), ma to bez względu na to, jaka liczba rzeczywista jest wybrana, ponieważ podczas oceny jej w F wynik zawsze będzie równy 2, co jest liczbą rzeczywistą.

Dlatego domeną danej funkcji jest wszystkie liczby rzeczywiste; to znaczy, a = r.

Teraz, gdy wiadomo już, że wynik funkcji jest zawsze równy 2, obraz funkcji jest tylko numer 2, dlatego sprzeczność funkcji można na nowo zdefiniować jako B = img (f) = 2.

Dlatego f: r → 2.

Przykład 2

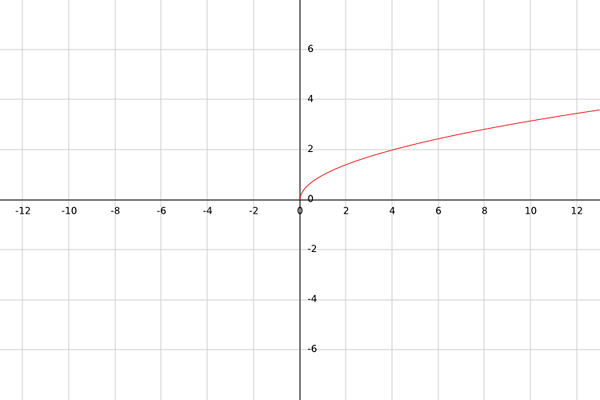
Niech g będzie rzeczywistą funkcją zdefiniowaną przez g (x) = √x.

Tak długo, jak obraz G nie jest znany, sprzeciwianie g wynosi b = r.

Dzięki tej funkcji należy wziąć pod uwagę, że korzenie kwadratowe są zdefiniowane wyłącznie dla liczb nieujemnych; to znaczy dla liczb większych lub równych niż zero. Na przykład √-1 nie jest liczbą rzeczywistą.

Dlatego opanowanie funkcji G musi być wszystkie liczby większe lub równe niż zero; to znaczy x ≥ 0.

Dlatego A = [0,+∞).

Aby obliczyć zakres, należy zauważyć, że każdy wynik g (x), ponieważ jest to pierwiastek kwadratowy, zawsze będzie większy lub równy. To znaczy, b = [0,+∞).

Podsumowując, g: [0,+∞) → [0,+∞).

Przykład 3

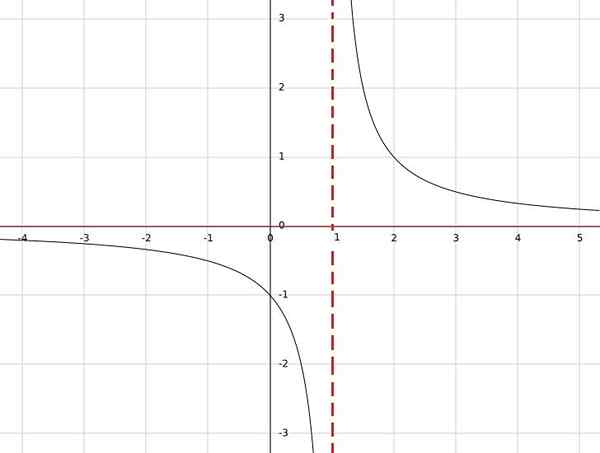
Jeśli masz funkcję h (x) = 1/(x-1), ta funkcja nie jest zdefiniowana dla x = 1, ponieważ w mianowniku uzyskano ją zero, a podział zero nie jest zdefiniowany.

Z drugiej strony, dla każdej innej wartości rzeczywistej wynik będzie liczbą rzeczywistą. Dlatego domena są reais z wyjątkiem jednego; to znaczy, a = r \ 1.

W ten sam sposób można zauważyć, że jedyną wartością, której nie można uzyskać w wyniku, jest 0, ponieważ aby ułamek był równy zero, licznik musi wynosić zero.

Dlatego obraz funkcji jest zbiorem wszystkich reais z wyjątkiem zeru, wówczas jest ono traktowane jako sprzeczne b = r 0.

Podsumowując, h: r \ 1 → r \ 0.

Obserwacje

Domena i obraz nie muszą być tym samym zestawem, jak pokazano w przykładach 1 i 3.

Gdy funkcja jest wykresem na płaszczyźnie kartezjańskiej, domena jest reprezentowana przez oś x, a sprzeczka lub zakres jest reprezentowany przez oś y.