Podziały, w których pozostałość wynosi 300
- 2172
- 207
- Matylda Duda
Jest wiele podziały, w których pozostałość wynosi 300. Oprócz cytowania niektórych z nich zostanie wyświetlona technika, która pomaga zbudować każdy z tych działów, co nie zależy od numeru 300.
Technika ta jest dostarczana przez algorytm podziału Euclida, który ustanawia: biorąc pod uwagę dwie liczby całkowite „N” i „B”, z „B” różniącymi się od zera (B ≠ 0), istnieją unikalne „Q” i „R. R. ", takie, że n = bq+r, gdzie 0 ≤" r " < |b|.
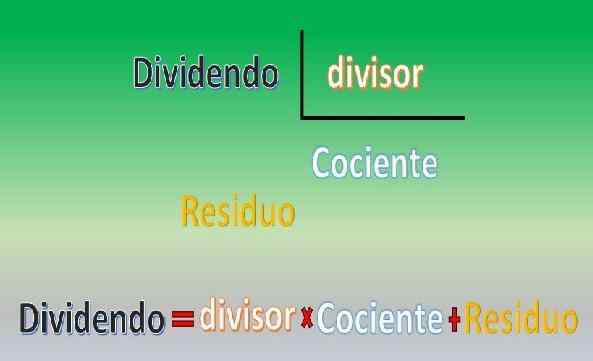
 Algorytm podziału Euclida
Algorytm podziału Euclida Liczby „N”, „B”, „Q” i „R” są odpowiednio nazywane dywidendy, dzielistą, ilorazem i pozostałościami (lub odpoczynkiem).
Należy zauważyć, że domagając się, aby pozostałość wynosiła 300, domyślnie mówi się, że wartość bezwzględna dzielnicy musi być większa niż 300, to znaczy: | b |> 300.
Przykłady podziałów, w których pozostałość wynosi 300
Poniżej znajdują się niektóre podziały, w których pozostałość wynosi 300; Następnie przedstawiono metodę budowy każdego podziału.
1- 1000 ÷ 350
Jeśli 1000 jest podzielone przez 350, można zauważyć, że iloraz wynosi 2, a pozostałość 300.
2-1500 ÷ 400
Dzieląc 1500 przez 400, uzyskuje się, że iloraz wynosi 3, a pozostałość 300.
3-3800 ÷ 700
Podczas tworzenia tego podziału będzie tak, że iloraz to 5, a pozostałość wyniesie 300.
4- 1350 ÷ (-350)
Kiedy ten podział zostanie rozwiązany, -3 jako iloraz i 300 jako pozostałość.
Jak budowane są te podziały?
Aby zbudować poprzednie podziały, musisz tylko prawidłowo użyć algorytmu podziału.
Cztery kroki do budowy tych działów to:
Może ci służyć: wypukły wielokąta: definicja, elementy, właściwości, przykłady1- Ustaw resztę
Jak chcesz, pozostałość wynosiła 300, R = 300 jest ustawiona.
2- Wybierz dzielnika
Ponieważ pozostałość wynosi 300, wybrany dzielnik musi być dowolnej liczby, tak że jego wartość bezwzględna jest większa niż 300.
3- Wybierz iloraz
W przypadku ilorazu możesz wybrać dowolną liczbę zero (q ≠ 0).
4- Dywidenda jest obliczana
Po ustaleniu pozostałości, dzielnicy i ilorazu są one zastąpione po prawej stronie algorytmu podziału. Rezultatem będzie liczba, która musi zostać wybrana jako dywidenda.
Z tymi czterem prostymi krokami możesz zobaczyć, jak zbudowano każdy oddział listy. We wszystkich tych R = 300 ustawiono.
Dla pierwszego podziału wybrano b = 350 i q = 2. Zastąpienie algorytmu podziału uzyskano 1000. Aby dywidenda musiała wynosić 1000.
Dla drugiego podziału ustalono B = 400 i Q = 3, tak że poprzez zastąpienie algorytmu podziału uzyskano 1500. W ten sposób ustalono, że dywidenda wynosi 1500.
Po trzeciej liczba 700 została wybrana jako dzielnik i jako iloraz numer 5. Podczas oceny tych wartości w algorytmie podziału uzyskano, że dywidenda musi być równa 3800.
W czwartym oddziale dzielnik równy -350, a iloraz równy -3. Gdy wartości te zostaną zastąpione w algorytmie podziału i rozwiązane, uzyskuje się, że dywidenda jest równa 1350.
Zgodnie z tymi krokami można zbudować wiele innych podziałów, w których pozostałość wynosi 300, uważając, gdy chcą używać liczb ujemnych.
Może ci służyć: Para uporządkowanaNależy zauważyć, że opisany powyżej proces budowy można zastosować do budowy podziałów z różnymi odpadami niż 300. Tylko liczba 300 zmieni się w pierwszym i drugim etapie, dla pożądanej liczby.
- « Działania i zachowania, które powodują zanieczyszczenie wody
- Organizacja polityczna Toltecs (rząd) »

