Jednolity rozkład kontynuuje charakterystykę, przykłady, aplikacje
- 2753
- 301
- Eugenia Czapla
Zmienna losowa ma Ciągłe jednolity rozkład Jeśli prawdopodobieństwo przyjmowania wartości, w odstępie skończonego [a, b], jest takie same dla dowolnego sub-interval o równej długości.
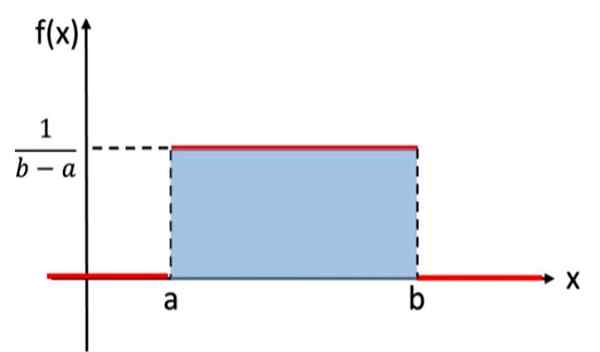
Rozkład ten jest analogiczny do dyskretnego jednolitego rozkładu, który przypisał do każdego wyniku losowego eksperymentu to samo prawdopodobieństwo, ale w tym przypadku zmienna, którą należy wziąć pod uwagę. Na przykład eksperyment, który polega na wybraniu losowej liczby rzeczywistej, między wartościami A i B, jest zgodny z jednolitym rozkładem. Tutaj masz swój wykres:
Rysunek 1. Wykres funkcji gęstości ciągłego znormalizowanego rozkładu jednolitego W notacji matematycznej ciągły jednolity rozkład ma funkcję gęstości zdefiniowaną jako funkcja dla kawałków lub przez sekcje, które można zapisać jako:
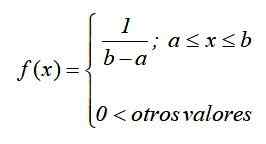
Wykres tej funkcji, znanej jako Funkcja krzywej lub gęstości, Jest to prostokąt, więc ciągły jednolity rozkład jest również znany jako Rozkład prostokątny I jest to najprostsze z ciągłych dystrybucji.
Obszar pod wykresem rozkładu prawdopodobieństwa jest równy 1 i zawsze przyjmuje wartości dodatnie. Jednolity rozkład spełnia te kryteria. Nie jest konieczne bezpośrednio integracja w celu sprawdzenia, czy obszar wynosi 1, ponieważ obszar zacienionego prostokąta na rycinie 1 można obliczyć za pomocą wzoru:
Obszar = podstawa x wysokość = (b - a) x [1/(b - a)] = 1
Znajomość obszaru pod krzywą gęstości jest bardzo ważna, ponieważ istnieje związek między obszarem a prawdopodobieństwem wystąpienia zdarzenia, który dla tego rozkładu jest określony w następnym rozdziale.
Ciągłe jednolite charakterystyki rozkładu
Ciągłe jednolity rozkład charakteryzuje się jego:
Funkcja gęstości
Niech x będzie ciągłą zmienną losową, która należy do przedziału [a, b], następnie:
Może ci służyć: transformacje liniowe: właściwości, jakie są użycie, typy, przykłady=\frac1b-a)
Funkcja dystrybucyjna
Za pomocą funkcji rozkładu obliczane jest prawdopodobieństwo, że zmienna losowa x przyjmuje wartość x z możliwych wartości interwału [a, b]. W przypadku rozkładu ciągłego jest on ogólnie obliczany w ten sposób:
=\int_a^xf(x)dx)
W przypadku ciągłego jednolitego rozkładu, prawdopodobieństwo f (x) jest równoważne z obszarem prostokąta, którego podstawa jest (x-a), a jego wysokość (b-a):
=\int_a^x\left&space;(\frac1b-a&space;\right&space;)dx=\fracx-ab-a)
Matematycznie, jeśli f (x) = pr (x = x) Poniższa funkcja jest ustalana przez części, zgodnie z poprzednim wynikiem:
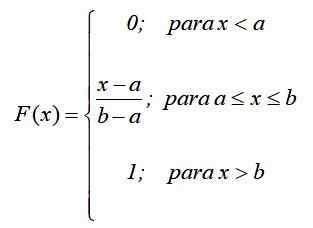
W ten sposób, co zostało wcześniej powiedziane: prawdopodobieństwo zależy tylko od wartości (x-a), a nie od jej lokalizacji w przedziale [a, b]. Wykres funkcji rozkładu jest:
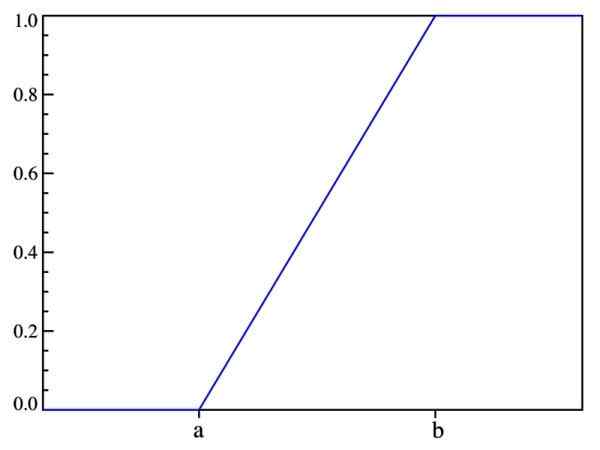Rysunek 2. Wykres funkcji rozkładu f (x). Źródło: Wikimedia Commons. Oczekiwana wartość, wariancja i odchylenie standardowe
Po przeprowadzeniu licznych eksperymentów z ciągłą zmienną losową, jego średnia wartość jest wywoływana wartość oczekiwana, Jest oznaczony jako E (x) i jest obliczany przez następującą całkę:
=\int_a^bxf(x)=\int_a^b\left&space;(\frac1b-a&space;\right&space;)xdx=\left&space;(\frac1b-a&space;\right&space;)\frac(b^2-a^2)2=\fraca+b2)
V (x) = e (x2) - BYŁY)2
Dlatego:
=\left&space;[\int_a^bx^2f(x)dx&space;\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2=\left&space;[\int_a^bx^2\left&space;(\fracb-a2&space;\right&space;)&space;dx\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2)
=\frac(b-a)^212)
D (x) = √ V (x)
=\sqrt\frac(b-a)^212)
Mediana, moda, symetria i ograniczenie
Można łatwo zweryfikować, że mediana, która jest centralną wartością jednolitego rozkładu, jest równa średniej, a ponieważ nie ma wartości, która jest powtarzana bardziej niż inne, ponieważ wszystkie są równie prawdopodobne w przedziale [a, b ], moda nie istnieje.
Jeśli chodzi o symetrię, równomierny rozkład jest symetryczny, a ograniczenie, w którym skoncentrowane są wartości wokół centrum, wynosi -6/5.
Może ci służyć: jakie są 7 elementów obwodu?Przykłady
Różne sytuacje można modelować poprzez ciągły rozkład, a tym samym przewidywać ich zachowanie. Oto kilka przykładów:
Przykład 1
Firma świadcząca usługi elektryczne zapewnia równomiernie rozproszone poziomy napięcia, między 123.0 V i 125.0 v. Oznacza to, że w ujęciu krajowym możliwe jest uzyskanie dowolnej wartości napięcia, która należy do tego przedziału.
Następnie, jak widać powyżej, wykres funkcji gęstości jest czerwony prostokąt:
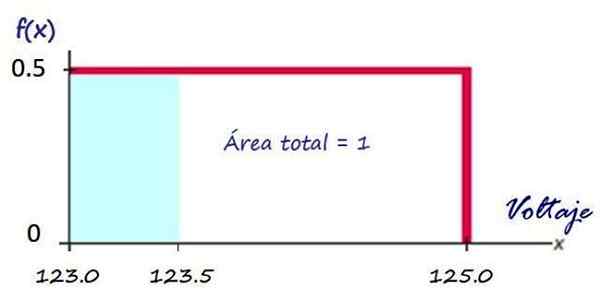Rysunek 3. Funkcja gęstości dla napięcia dostarczanego przez firmę elektryczną. Źródło: f. Zapata. Obliczanie prawdopodobieństwa posiadania napięcia w danym przedziale jest bardzo łatwe, na przykład, jakie jest prawdopodobieństwo, że firma wyśle napięcie mniejsze niż 123.5 v?
To prawdopodobieństwo jest równoważne z obszarem zacienionego prostokąta na niebiesko:
P (x<123.5) = (123.5 −123.0)x 0.5 = 0.25
I jakie jest prawdopodobieństwo, że dostarczone napięcie jest większe niż 124.0 v?
Ponieważ całkowita powierzchnia wynosi 1, poszukiwane prawdopodobieństwo to:
P (x> 124.0 V) = 1 - (1 × 0.5) = 0.5
Ma sens, od 124.0 jest dokładnie wartością w środku interwału.
Przykład 2
Pewna zmienna losowa X ma jednolity rozkład w przedziale [0.100]. Określić:
a) Prawdopodobieństwo, że wartość x jest mniejsza niż 22.
b) prawdopodobieństwo, że x przyjmuje wartości między 20 a 35.
c) oczekiwana wartość, wariancja i odchylenie standardowe tego rozkładu.
Odpowiedz
Jest to określone podobnie do poprzedniego przykładu, ale najpierw musimy określić wysokość prostokąta, pamiętając, że całkowita powierzchnia musi być równa 1:
Obszar = 100 × wysokość = 1
Dlatego prostokąt ma wysokość równą 1/100 = 0.01
Może ci służyć: decagon: regularne, nieregularne, nieruchomości, przykładyP (x<22) = 22×0.01 = 0.22
Odpowiedź b
Zakładane prawdopodobieństwo jest równoważne z obszarem prostokąta, którego szerokość wynosi (35–20) i którego wysokość wynosi 0.01:
P (22 Jeśli wolisz przejść bezpośrednio do powyższej funkcji rozkładu, musisz po prostu wymienić wartości w: P (20 ≤ x 35) = f (35) -F (20) Z f (x) podanym przez: F (x) = (x-a) / (b-a) Wartości, które należy wprowadzić, to: A = 0 B = 100 F (35) = (35-0) / (100-0) = 0.35 F (20) = (20-0) / (100-0) = 0.20 P (20 ≤ x 35) = 0.35-0.20 = 0.piętnaście Oczekiwana wartość to: E (x) = (a+b)/2 = (100+0)/2 = 50 Wariancja to: V (x) = (b-a)2/12 = (100-0)2/12 = 833.33 A odchylenie standardowe to: D (x) = √833.33 = 28.87 Ten rozkład jest przydatny, gdy przeprowadzane są procesy symulacji statystycznej lub podczas pracy w zdarzeniach, których częstotliwość wyglądu jest regularna. Niektóre języki programowania generują liczby losowe między 0 a 1, i jak widać na podstawie poprzednich przykładów, rozkład obserwowanych prawdopodobieństw jest jednolity. W takim przypadku przedział do rozważenia wynosi [0,1]. Jeśli masz eksperyment, w którym zdarzenia mają regularność, jak wyjaśniono powyżej, w zasadzie możesz przypisać każdemu tak samo prawdopodobieństwo wystąpienia. W takim przypadku probabilistyczny model jednolitego rozkładu zawiera informacje do analizy. Jednolity rozkład jest również stosowany w zaokrąglaniu różnic między obserwowanymi wartościami a wartościami rzeczywistymi zmiennej, zakładając jednolity rozkład błędu w danym przedziale, zgodnie z zaokrąglaniem, zwykle wynoszącym -0,5 do +0,5.Odpowiedź c
Aplikacje
Losowe liczby
Arbitralne pobieranie próbek dystrybucji
Zaokrąglenie błędu
Bibliografia