Wzór ekspansji powierzchni, współczynniki i przykłady

powierzchowne rozszerzenie Jest to rozszerzenie, które występuje, gdy obiekt doświadcza zmian jego powierzchni z powodu zmienności temperatury. Wynika to z charakterystyk materiału lub jego geometrycznego kształtu. Rozszerzenie przeważa w dwóch wymiarach w tej samej proporcji.

Na przykład w arkuszu, gdy istnieje zmienność temperatury, jest to powierzchnia tego samego, która cierpi z powodu największej zmiany z powodu rozszerzenia termicznego.

Powierzchnia metalowej płyty, która jest zwykle widoczna na ulicach. Źródło: Pixabay.

Arkusz metalowy poprzedniej figury zwiększa jego szerokość, a długość znacząca, gdy jest podgrzewana przez promieniowanie słoneczne. Przeciwnie, oba zmniejszają się znacznie po schłodzeniu z powodu spadku temperatury otoczenia.

Z tego powodu, gdy płytki są zainstalowane na jednym piętrze, niektóre krawędzie z innymi nie powinny zostać uderzone, ale musi istnieć przestrzeń separacyjna zwana tablicą rozszerzania.

Ponadto przestrzeń ta jest wypełniona specjalną mieszanką, która ma pewien stopień elastyczności, zapobiegając pękanie płytek z powodu silnych ciśnienia, jakie może wytwarzać rozszerzenie termiczne.

[TOC]

Co to jest powierzchowne rozszerzenie?

W stałym materiale atomy utrzymują swoje mniej lub bardziej ustalone pozycje względne wokół punktu równowagi. Jednak ze względu na pobudzenie termiczne zawsze otaczają wokół niego.

Poprzez zwiększenie temperatury wzrasta również oscylacja termiczna, powodując zmianę pozycji oscylacji średniej. Wynika to z faktu, że potencjał łącza nie jest dokładnie paraboliczny i ma asymetrię wokół minimum.

Poniżej znajduje się liczba, która przedstawia energię wiązania chemicznego w zależności od odległości międzyatomicznej. Pokazana jest również całkowita energia oscylacji w dwóch temperaturach i sposób poruszania się centrum oscylacji.

Może ci służyć: Pascal Tonel: Jak to działa i eksperymenty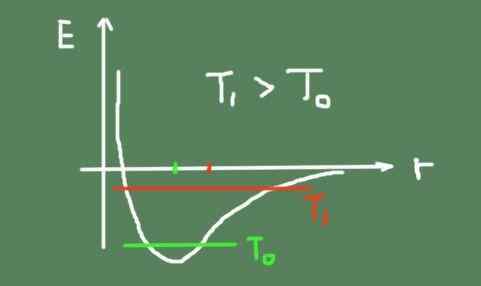Połącz wykres energii w porównaniu do odległości międzyatomicznej. Źródło: Self Made.

Powierzchowne rozszerzenie i jego współczynnik

Aby zmierzyć powierzchowne rozszerzenie, zaczynamy od początkowego obszaru A i początkowej temperatury t, z którego obiektu ma się zmierzyć rozszerzenie.

Załóżmy, że ten obiekt jest blaszką obszaru A, a jego grubość jest znacznie niższa niż pierwiastek kwadratowy obszaru a. Arkusz jest poddawany zmianie temperatury ΔT, tak że końcowa temperatura tej samej po ustaleniu równowagi termicznej ze źródłem ciepła będzie t '= t+ δt.

Podczas tego procesu termicznego powierzchnia zmieni się również na nową wartość przy '= a + δA. Zatem współczynnik rozszerzenia powierzchniowego σ jest zdefiniowany jako stosunek między względną zmiennością powierzchni na jednostkę zmienności temperatury.

Poniższy wzór określa powierzchowny współczynnik rozszerzenia σ:

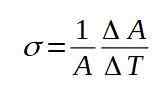
Powierzchowny współczynnik rozszerzenia σ jest praktycznie stały dla szerokiego zakresu wartości temperatury.

Ze względu na definicję σ jego wymiary są temperaturą odwrotną. Jako jednostka jest zwykle używana ° C^-1.

Współczynnik rozszerzenia powierzchni dla różnych materiałów

Następnie podamy listę powierzchownego współczynnika rozszerzenia dla niektórych materiałów i elementów. Współczynnik oblicza się w normalnym ciśnieniu atmosferycznym na podstawie temperatury otoczenia 25 ° C, a jego wartość jest uważana za stały w zakresie δT od -10 ° C do 100 ° C.

Jednostka powierzchownego współczynnika rozszerzenia będzie (° C)^-1

- Stal: σ = 24 ∙ 10^-6 (° C)^-1

- Aluminium: σ = 46 ∙ 10^-6 (° C)^-1

Może ci służyć: magnetyzacja: moment magnetyczny orbital i spin, przykłady

- Złoto: σ = 28 ∙ 10^-6 (° C)^-1

- Miedź: σ = 34 ∙ 10^-6 (° C)^-1

- Mosiądz: σ = 36 ∙ 10^-6 (° C)^-1

- Żelazo: σ = 24 ∙ 10^-6 (° C)^-1

- Szkło: σ = (14 do 18) ∙ 10^-6 (° C)^-1

- Kwarc: σ = 0,8 ∙ 10^-6 (° C)^-1

- Diamond: σ = 2 ,, 4 ∙ 10^-6 (° C)^-1

- Ołów: σ = 60 ∙ 10^-6 (° C)^-1

- Drewno dębowe: σ = 108 ∙ 10^-6 (° C)^-1

- PVC: σ = 104 ∙ 10^-6 (° C)^-1

- Włókno węglowe: σ = -1,6 ∙ 10^-6 (° C)^-1

- Beton: σ = (16 do 24) ∙ 10^-6 (° C)^-1

Większość materiałów rozciąga się ze wzrostem temperatury. Jednak niektóre materiały, takie jak włókno węglowe, spełniają wzrost temperatury.

Rozwiązane przykłady powierzchownego rozszerzenia

Przykład 1

Płyta stalowa ma wymiary 3 m x 5m. Rano i w cieniu jego temperatura wynosi 14 ° C, ale w południe słońce ogrzewa do 52 ° C. Znajdź ostateczny obszar płyty.

Rozwiązanie

Zaczynamy od definicji powierzchownego współczynnika rozszerzenia:

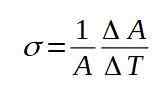
Stąd usuwamy zmienność w tym obszarze:

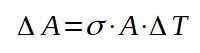
Następnie przystępujemy do wymiany odpowiednich wartości, aby znaleźć wzrost powierzchni wraz z wzrostem temperatury.

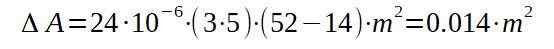
Oznacza to, że ostateczny obszar wyniesie 15 014 metrów kwadratowych.

Przykład 2

Pokazać, że powierzchowny współczynnik rozszerzenia jest około dwa razy większy niż liniowy współczynnik rozszerzenia.

Rozwiązanie

Załóżmy, że zaczynamy od prostokątnej płyty o wymiarach szerokości LX i długiej, wówczas jej początkowa powierzchnia wyniesie a = lx ∙ ly

Może ci służyć: skale termometryczne

Kiedy płyta cierpi na wzrost temperatury δT, wówczas jej wymiary również wzrosną, ponieważ jego nowa szerokość Lx i nowa ly ​​„długa, tak że jej nowym obszarem będzie„ = lx '∙ ly'

Zmienność poniżona przez powierzchnię płytki z powodu zmiany temperatury będzie wtedy

ΔA = lx '∙ ly' - lx ∙ ly

gdzie lx '= lx (1 + α δT) i ly' = ly (1 + α ΔT)

Oznacza to, że zmiana powierzchni w zależności od współczynnika rozszerzenia liniowego i zmiana temperatury będzie:

ΔA = LX (1 + α δT) ∙ LY (1 + α δT) - LX ∙ ly

Można to przepisać jako:

ΔA = lx ∙ ly ∙ (1 + α δT) ² - lx ∙ ly

Rozwijanie kwadratu i mnożenie mamy następujące:

I

Ponieważ α jest rzędu 10^-6, Podnosząc go kwadratem, jest to zamówienie 10^-12. Zatem kwadratowy termin w poprzednim wyrażeniu jest nikczemny.

Wówczas wzrost obszaru może podchodzić:

ΔA ≈ 2α δt lx ∙ ly

Ale wzrost powierzchni w zależności od powierzchownego współczynnika rozszerzenia wynosi:

ΔA = γ δT a

Od miejsca, w którym wywnioskowane jest wyrażenie, które wiąże współczynnik rozszerzenia liniowego do powierzchownego współczynnika rozszerzenia.

γ ≈ 2 ∙ α

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. Mac Graw Hill. 422-527
2. Giancoli, zm. 2006. Fizyka: zasady z aplikacjami. 6th. Wydanie. Prentice Hall. 238-249.