Różnica między okrągiem a obwodem (z przykładami)

Różnica między okrągiem a obwodem Jest to następujące: okrąg jest płaską, wyprofilowaną lub ograniczoną powierzchnią przez okrąg, a ta ostatnia jest płaską krzywą.

Często obie pojęcia są zdezorientowane, ponieważ są powiązane, ale zawsze musisz pamiętać, że obwód jest krawędzią koła, podczas gdy zawiera obwód i wszystkie punkty wnętrza.

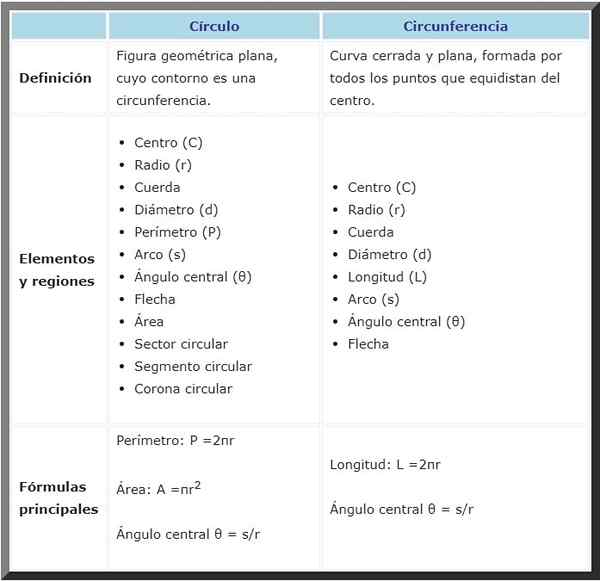
Oba mają wiele wspólnych elementów, takich jak środek, promień i średnica, między innymi, zgodnie z następującą tabelą porównawczą:

	Koło	Obwód
Definicja	Płaska figura geometryczna, której kontur jest obwód.	Zamknięta i płaska krzywa, utworzona przez wszystkie punkty, które są równoległe w środku.
Elementy i regiony	Centrum (c) Radio (R) Lina Średnica (d) Obwód (P) ARC (y) Kąt centralny (Θ) Strzałka Obszar Sektor okrągły Segment okrągły Okrągła korona	Centrum (c) Radio (R) Lina Średnica (d) Długość (l) ARC (y) Centralna długość (Θ) Strzałka
Formuły	Obwód: p = 2π⋅R Obszar: a =πR2 Centralny kąt: Θ= s/r	Długość: l = 2π⋅R Centralny kąt: Θ= s/r

[TOC]

Koło: definicja, cechy i części

Koło jest płaską postacią geometryczną, która obejmuje wszystkie punkty obwodu, które tworzą kontur, a także wszystkie punkty wewnętrzne.

Z tego powodu charakteryzuje się posiadaniem:

-Krawędź lub obwód, który jest obwodem koła.

-Powierzchowny obszar.

Elementy koła

Każde koło ma następujące części lub elementy:

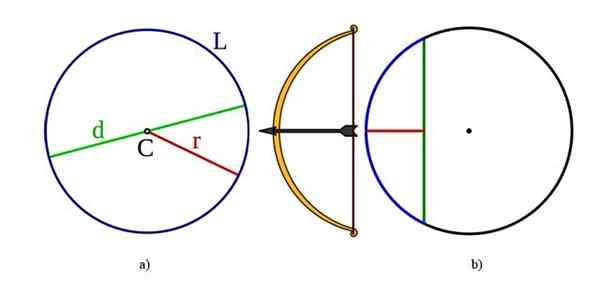Elementy okręgu, również wspólne dla obwodu: po lewej w A) są środkowa D, średnica D, promień R i długość l l. Tuż na b) są lina i sagita lub strzałka. Źródło: Wikimedia Commons.

Centrum: Co to jest punkt C, który równoległe wszystkie punkty krawędzi.

Może ci służyć: Arc (geometria): miara, rodzaje łuków, przykłady

Lina: segment, który łączy dwa punkty krawędzi koła. Na rysunku b) po prawej stronie jest to ciemniejszy zielony segment.

Średnica: lżejszy zielony segment, oznaczony „d” na rysunku a), który łączy dwa punkty krawędzi i jednocześnie przechodzi przez środek. Średnica jest również liną, najdłuższą ze wszystkich, więc jest znana jako Główna lina.

Radio: oznaczone przez „r” na rysunku a), to czerwony segment łączy się na środek koła z punktem krawędzi. Jego miara to połowa średnicy.

Ukłon: Część konturu, która znajduje się między dwoma punktami tego, na niebiesko na rysunku B).

Kąt centralny: Jest to kąt, którego wierzchołek znajduje się w środku lub boki to radiotelefony koła.

Strzałka: segment prostopadły do ​​liny (na czerwono na rysunku b), która łączy się na środek liny z punktem krawędzi.

Długość lub obwód: Jest miarą konturu koła, oznaczonego l. Zależy to od radia R i jest proporcjonalne do liczby irracjonalnej π:

π = 3.1416 ..

Aby:

L = 2π⋅R

Regiony okrągłe

Będąc płaską postacią, okrąg ma całkowitą powierzchnię, a także różne regiony. Najbardziej znane są następujące:

Obszar okręgu: Jest proporcjonalny do kwadratu promienia, a stała proporcjonalności jest liczba π.

Nazywając obszar okręgu, wyraża się to jako:

A = πr²

Segment okrągły: Jest to część okręgu ograniczona przez niebieski łuk i ciemnozieloną linę na rysunku B.

Może ci służyć: kąty uzupełniające: co to są, obliczenia, przykłady, ćwiczenia

Sektor okrągły: Jest to również region okręgu, ale zawarty między dwoma radia i odpowiednim łukiem.

Okrągła korona: Ma kształt pierścienia i jest ograniczony dwoma koncentrycznymi obwodami, poza radiem menor i wewnątrz burmistrza radiowego.

Obwód: dEfinition, cechy i części 

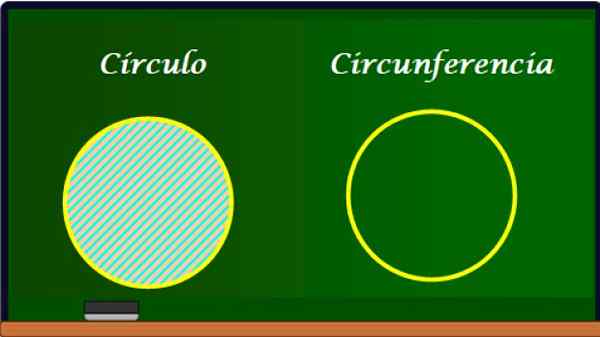Krąg i jego obwód. Źródło: f. Zapata.

Obwód jest krawędzią koła i dlatego ma wiele wspólnych elementów. Jednak obwód nie ma obszaru, ponieważ ponieważ jest to krzywa, ma tylko długość L.

Obwód jest formalnie zdefiniowany jako zbiór wszystkich punktów równa się z innego punktu znanego jako środek.

Punkty wewnętrzne nie są uwzględnione, ponieważ odpowiadają one okręgu.

Elementy obwodu

Wiele elementów obwodu jest takich samych jak elementy koła, z wyłączeniem tych, które odnoszą się do obszarów i regionów, więc górna liczba służy jako odniesienie.

Mamy wtedy:

Centrum: oznaczone przez c, a czasem także jako o, wszystkie punkty obwodu zachowują z nim tę samą odległość.

Lina: segment, który łączy dwa punkty należące do obwodu.

Średnica: Dołącza również do dwóch punktów obwodu, ale zawsze przechodzi przez środek tego samego.

Radio: Jest to odległość między środkiem a dowolnym punktem obwodu.

Ukłon: To część obwodu.

Kąt centralny: To kąt z wierzchołkiem w środku C i dwiema równymi stronami, które mierzą tak jak radio.

Strzałka: segment prostopadły do ​​liny, która łączy się z środkiem z odpowiednim punktem obwodu.

Może ci służyć: Zasada multiplikatywna: Techniki zliczania i przykłady

Długość lub obwód: Jest to miara obwodu, która, jak widzieliśmy, jest proporcjonalna do liczby π = 3.1416… i jest obliczany przez formułę:

L = 2π⋅R

Równanie obwodu

Punkt p należy do obwodu, o ile jego odległość do innego punktu C jest równa R, radio.

Każdy punkt na płaszczyźnie kartezjański ma współrzędne (X, y) i kwadrat odległości D Między dwoma z nich, p₁(X₁,I₁) I p₂(X₂,I₂), jest podawany przez formułę:

D₂² = (x₂ - X₁)² +  (I₂ - I₁)²

Przejdźmy do punktu współrzędnych (x, y) i koordynacji punktu c (h, k). Zastąpienie poprzednie równanie byłoby takie:

(X - h)² +  (Y- k)² = r²

To jest równanie obwodu, które spełnia każdy punkt na nim. Jeśli środek obwodu pokrywa się z pochodzeniem układu współrzędnych, wówczas h = k = 0 i równanie jest uproszczone:

X² + I² = r²

Spójrzmy na przykład używania równania i odpowiedz na ten problem: czy punkt (4.6) należy do obwodu (x - 1)² +  (i - 2)² = 25?

Aby dowiedzieć się, że współrzędne punktu w równaniu są zastąpione, a jeśli jest to równość, wówczas punkt należy do obwodu:

(4 - 1)² +  (6 - 2)² = 3² + 4² = 9 + 16 = 25

I rzeczywiście, jak 25 = 25, stwierdza się, że (4.6) należy do obwodu.

Bibliografia

1. Bezpłatne samouczki matematyczne. Obszar i obwód kalkulatora okręgu - geometrii. Odzyskane z: Analezemath.com.
2. Odniesienie do otwartego matematyki. Obwód, obwód koła. Odzyskane z: Mathpenref.com.
3. Naukowe. Jak znaleźć obwód koła. Odzyskane z: naukowe.com.
4. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.