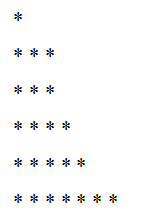Rozkład addytywny

Rozkład addytywny pozytywnej liczby całkowitej jest wyrażanie go jako sumę dwóch lub więcej liczb dodatnich. Zatem mamy, że liczba 5 może to wyrazić jako 5 = 1+4, 5 = 2+3 lub 5 = 1+2+2. Każdy z tych sposobów pisania numer 5 nazywamy rozkładem addytywnym.

Jeśli zwrócimy uwagę, widzimy, że wyrażenia 5 = 2+3 i 5 = 3+2 reprezentują ten sam skład; Oba mają te same liczby. Jednak tylko w przypadku komfortu jest zwykle zapisywane każda z reklam zgodnie z kryteriami od najmniejszej do największej.

Rozkład addytywny

Jako kolejny przykład możemy wziąć numer 27, który możemy to wyrazić jako:

27 = 7+10+10

27 = 9+9+9

27 = 3+6+9+9

27 = 9+18

Rozkład addytywny jest bardzo przydatnym narzędziem, które pozwala nam wzmocnić naszą wiedzę na temat systemów numeracji.

Kanoniczny rozkład addytywny

Kiedy mamy liczbę więcej niż dwóch liczb, konkretna forma ich rozkładu znajduje się w wielokrotnościach 10, 100, 1000, 10 000 itp., które to nadają. Ten sposób pisania dowolnej liczby nazywa się kanonicznym rozkładem addytywnym. Na przykład numer 1456 może go rozłożyć w następujący sposób:

1456 = 1000 + 400+ 50 + 6

Jeśli mamy numer 20 846 295, Twój kanoniczny rozkład addytywny będzie:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Dzięki temu rozkładowi widzimy, że wartość danej cyfry jest podana przez pozycję, którą zajmuje. Weźmy jako przykład liczby 24 i 42:

24 = 20 + 4

42 = 40 +2

Tutaj widzimy, że w 24 2 ma wartość 20 jednostek i na 4 wartość 4 jednostek; Z drugiej strony, w 42 4 ma wartość 40 jednostek i 2 z dwóch jednostek. Zatem, chociaż obie liczby używają tych samych cyfr, ich wartości są zupełnie inne według pozycji, którą zajmują.

Może ci służyć: x kwadrat

Aplikacje

Jedną z zastosowań, które możemy podać do rozkładu addytywnego, jest pewne rodzaje demonstracji, w których bardzo przydatne jest postrzeganie pozytywnej liczby całkowitej jako sumę innych.

Przykładowe twierdzenie

Weźmy jako przykład następujące twierdzenie z ich odpowiednimi demonstracjami.

- Bądź z całą liczbą 4 cyfr, a następnie z jest podzielna przez 5, jeśli jego liczba odpowiadająca jednostkom wynosi zero lub pięć.

Demonstracja

Pamiętajmy, jaka jest podzielność. Jeśli mamy liczby „A” i „B”, mówimy, że „A” dzieli „B”, jeśli istnieje liczba całkowita „C”, taka, że ​​B = A*C.

Jedna z właściwości podziałalności mówi nam, że jeśli „a” i „b” są podzielne między „c”, to odejmowanie „a-b” jest również.

Być z całą liczbą 4 cyfr; Dlatego możemy napisać do Z i Z = ABCD.

Używając kanonicznego rozkładu addytywnego, musimy:

Z = A*1000 + B*100 + C*10 + D

Oczywiste jest, że*1000 + b*100 + c*10 jest podzielny między 5. Dlatego mamy, że Z jest podzielny między 5, jeśli z - (a*1000 + b*100 + c*10) jest podzielny między 5.

Ale z - (a*1000 + b*100 + c*10) = d i d to pojedyncza liczba rysunków, więc jedynym sposobem na podzielenie się między 5 jest to, że jest to 0 lub 5.

Dlatego z jest podzielne między 5, jeśli d = 0 lub d = 5.

Zauważ, że jeśli Z ma n cyfry, demonstracja jest dokładnie taka sama, to tylko zmienia się, że teraz napisześmy z = a₁DO₂… DO_N A celem byłoby to udowodnienie_N ma zero lub pięć.

Partycje

Mówimy, że partycja pozytywnej liczby całkowitej jest sposobem, w jaki możemy napisać liczbę jako suma dodatnich liczb całkowitych.

Może ci służyć: Radio zbieżności: definicja, przykłady i ćwiczenia rozwiązane

Różnica między rozkładem addytywnym a partycją polega na tym, że podczas gdy w pierwszym poszukiwano, że przynajmniej można go podzielić na dwa lub więcej, w partycji to ograniczenie.

Dlatego mamy następujące czynności:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+2+2

Powyższe są partycje 5.

Oznacza to, że całe rozkład addytywny jest partycją, ale nie cała partycja jest koniecznie rozkładem addytywnym.

W teorii liczb podstawowe twierdzenie arytmetycznego gwarantuje, że każda liczba całkowita może być pisana wyjątkowo jako produkt kuzynów.

Po badaniu partycji celem jest ustalenie, ile sposobów można zapisać pozytywną liczbę całkowitą jako sumę innych liczb całkowitych. Dlatego definiujemy funkcję partycji, jak przedstawiono poniżej.

Definicja

Funkcja partycji p (n) jest zdefiniowana jako liczba sposobów, w jakie dodatnia liczba całkowita n może być zapisana jako suma liczb całkowitych.

Wracając do przykładu 5, musimy:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+1+3

5 = 1+2+2

5 = 1+1+1+2

5 = 1+1+1+1+1

W ten sposób P (5) = 7.

Wykresy

Zarówno partycje, jak i rozkłady addytywne liczby N mogą być reprezentowane geometrycznie.  Załóżmy, że mamy addytywne rozkład n. W tym rozłożeniu dodanie można naprawić, aby członkowie sum. Więc jest warte:

n = a₁ + Do₂ + Do₃ +… + A_R z

Do₁ ≤ a₂ ≤ a₃ ≤ ... ≤ a_R.

Możemy wykresy powiedział rozkład w następujący sposób: W pierwszym rzędzie zaznaczamy₁-Punkty, a następnie następujące wyznaczamy₂-Punkty i tak dalej, aż sięgają_R.

Może ci służyć: nierówność trójkąta: demonstracja, przykłady, rozwiązane ćwiczenia

Weźmy jako przykład numer 23 i jego następny rozkład:

23 = 5 + 4 + 7 + 3 + 1 +3

Zamawiamy ten rozkład i mamy:

23 = 1 + 3 + 3 + 4+ 5 + 7

Jego odpowiedni wykres byłby:

Podobnie, jeśli zamiast tego przeczytamy ten wykres pionowo, możemy uzyskać rozkład, który prawdopodobnie różni się od poprzedniego. W przykładzie 23 wyróżnia się następujący:

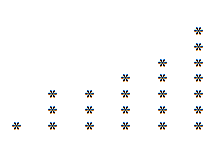
Mamy więc 23, możemy to również napisać jako:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.