Kolejne pochodne

Jakie są kolejne pochodne?

 kolejne pochodne Są te pochodzące z funkcji po drugiej pochodnej. Proces obliczania kolejnych pochodnych jest następujący: istnieje funkcja F, którą możemy wyprowadzić i uzyskać funkcję pochodną f '. Do tej pochodnej F możemy go ponownie wyprowadzić, uzyskując (f ')'.

Ta nowa funkcja nazywa się drugą pochodną; Wszystkie pochodne obliczone z drugiego są kolejne; Te, zwane również wyższym rzędem, mają duże zastosowania, takie jak podawanie informacji o udarze wykresu funkcji, test drugiej pochodnej dla celów względnych i określenie serii nieskończoności.

Definicja

Za pomocą notacji Leibniz mamy, że pochodna funkcji „Y” w odniesieniu do „x” jest DY/DX. Aby wyrazić drugą pochodną „y” za pomocą notacji Leibniz, piszemy w następujący sposób:

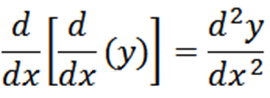
Ogólnie rzecz biorąc, możemy wyrazić kolejne pochodne w następujący sposób z notacją Leibniz, gdzie n reprezentuje porządek pochodnej.

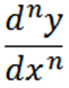
Inne zastosowane notacje są następujące:

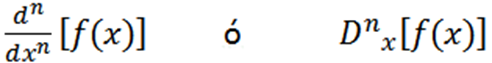
Niektóre przykłady, w których możemy zobaczyć różne notacje:

Przykład 1

Uzyskaj wszystkie pochodne funkcji F zdefiniowanej przez:

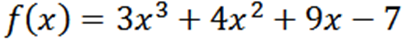
Korzystając z zwykłych technik polecenia, mamy, że F jest:

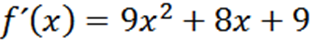
Powtarzając proces, możemy uzyskać drugą pochodną, ​​trzecią pochodną i tak dalej.

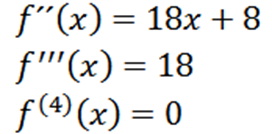
Zauważ, że czwarta pochodna wynosi zero, a pochodna zerowa wynosi zero, więc musimy:

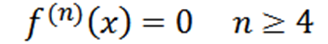
Przykład 2

Oblicz czwarty pochodzący z następującej funkcji:

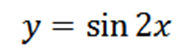
W rezultacie uzyskanie danej funkcji:

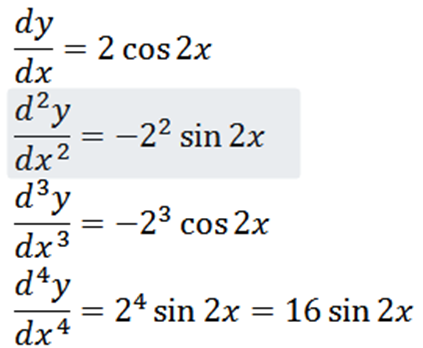
Prędkość i przyspieszenie

Jedną z motywacji, które doprowadziły do ​​odkrycia pochodnej, było poszukiwanie definicji natychmiastowej prędkości. Formalna definicja jest następująca:

Może ci służyć: liczby Primo: Charakterystyka, przykłady, ćwiczenia

Niech y = f (t) funkcja, której wykres opisuje trajektorię cząstki w jednej chwili T, Następnie jego prędkość w natychmiastowym t jest podana przez:

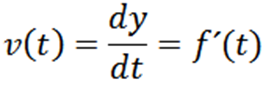
Po uzyskaniu prędkości cząstki możemy obliczyć natychmiastowe przyspieszenie, które jest zdefiniowane w następujący sposób:

Natychmiastowe przyspieszenie cząstki, której trajektoria jest podana przez y = f (t) to:

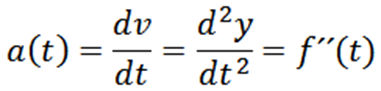
Przykład 1

Cząstka porusza się po linii zgodnie z funkcją pozycji:

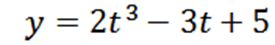
Gdzie „y” mierzy się w metrach i „t” w sekundach.

• W jakim momencie Twoja prędkość wynosi 0?
• W jakim momencie jego przyspieszenie wynosi 0?

Wyprowadzając funkcję pozycji „Y”, mamy, że jej prędkość i przyspieszenie są odpowiednio podawane przez:

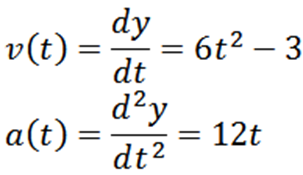
Aby odpowiedzieć na pierwsze pytanie, wystarczy ustalić, kiedy funkcja v V wynosi zero; to jest:

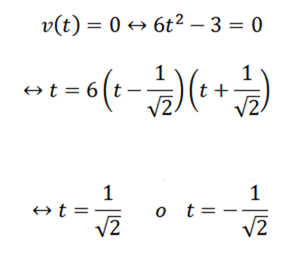
Następnym pytaniem jest analogiczne:

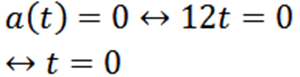
Przykład 2

Cząstka porusza się po linii zgodnie z następującym równaniem ruchu:

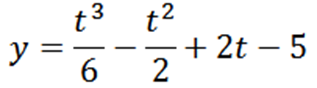
Określ „t, y” i „v”, gdy a = 0.

Wiedząc, że prędkość i przyspieszenie są podane przez

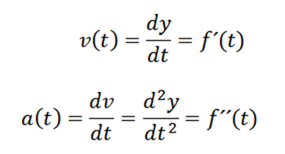
Dostajemy i uzyskujemy:

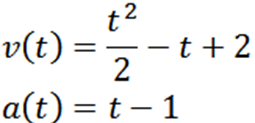
Robiąc a = 0, mamy:

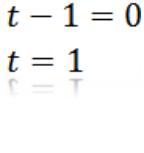
Gdzie możemy wywnioskować, że wartość t, tak aby A jest równe zero, wynosi t = 1.

Następnie, oceniając w t = 1 funkcja pozycji i funkcji, musimy:

Aplikacje

Prowadzenie Mplícita

Kolejne pochodne można również uzyskać przez niejawne wyprowadzenie.

Przykład

Biorąc pod uwagę następującą elipsę, znajdź „y”:

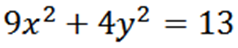
Domyślnie pochodzi od X, mamy:

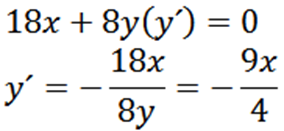
Następnie, ponowne wyróżnienie w odniesieniu do X daje nam:

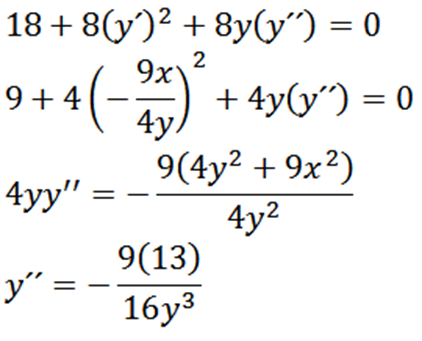
Wreszcie mamy:

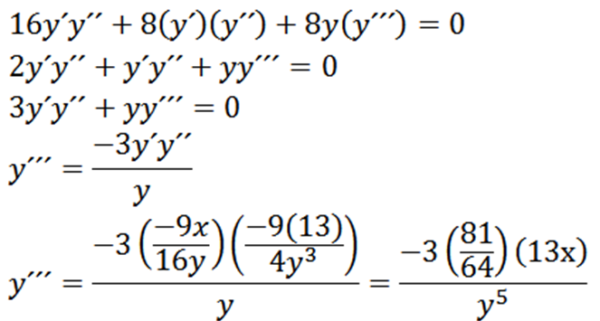
Względne skrajności

Kolejnym zastosowaniem, które możemy podać do pochodnych drugiego zamówienia, jest obliczenie względnych końców funkcji.

Może ci służyć: ile osi symetrii ma koło?

Kryteria pierwszej pochodnej dla skrajności lokalnych mówią nam, że jeśli mamy ciągłą funkcję F w odstępie (a, b) i istnieje c, który należy do wspomnianego przedziału, tak że jest unieważnione w C (to znaczy, że c jest punktem krytycznym), może wystąpić jeden z tych trzech przypadków:

• Jeśli f '(x)> 0 dla dowolnego x należącego do (a, c) i f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
• Jeśli f '(x) 0 dla x należące do (c, b), to f (c) jest minimum lokalnym.
• Jeśli f '(x) ma ten sam znak w (a, c) i w (c, b), oznacza to, że f (c) nie jest lokalnym końcem.

Stosując kryteria drugiej pochodnej.

Kryterium drugiego dryfu mówi nam, że jeśli f '(c) = 0 i że f "(x) jest ciągłe w (a, b), zdarza się, jeśli f" (c)> 0, to f (c) to a Minimum lokalne i jeśli f "(c) < 0 entonces f(c) es un máximo local.

Jeśli f "(c) = 0, nie możemy niczego zakończyć.

Przykład

Biorąc pod uwagę funkcję f (x) = x⁴ + (4/3) x³ - 4x², Znajdź maksymalny i minimalny krewny F Stosowanie kryteriów drugiej pochodnej.

Najpierw obliczamy f '(x) i f "(x) i mamy:

f '(x) = 4x³ + 4x² - 8x

f "(x) = 12x² + 8x - 8

Teraz f '(x) = 0 tak, i tylko wtedy, gdy 4x (x + 2) (x - 1) = 0, i dzieje się to, gdy x = 0, x = 1 lub x = - 2.

Aby ustalić, czy uzyskane liczby krytyczne są ekstremami względnymi, po prostu oceniają w F ”, a tym samym obserwować jego znak.

Może ci służyć: heptagon

f "(0) = - 8, więc f (0) jest lokalnym maksimum.

f "(1) = 12, więc f (1) jest lokalnym minimum.

f "(- 2) = 24, więc F (- 2) jest lokalnym minimum.

Seria Taylor

Być funkcją zdefiniowaną w następujący sposób:

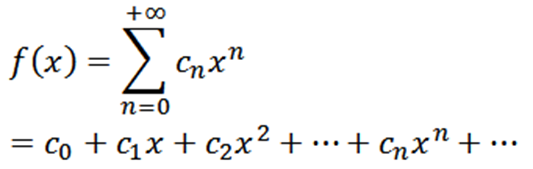
Ta funkcja ma promień konwergencji r> 0 i wyprowadziła się ze wszystkich zamówień w (-r, r). Kolejne pochodne F Daj nam:

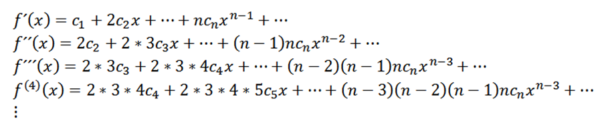
Biorąc x = 0, możemy uzyskać wartości C_N w zależności od jego pochodnych w następujący sposób:

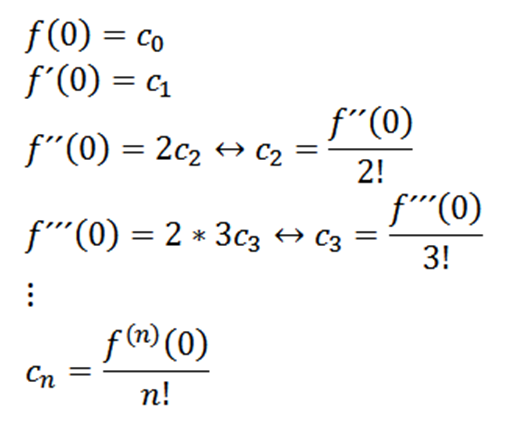
Jeśli weźmiemy n = 0 jako funkcję f (tj. F^0 = f), możemy przepisać funkcję w następujący sposób:

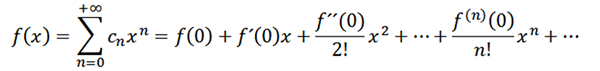
Rozważmy teraz tę funkcję jako serię mocy przy x = a:

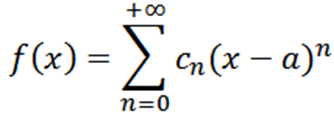
Jeśli przeprowadzimy analizę analogiczną do poprzedniej, musielibyśmy napisać funkcję F jako:

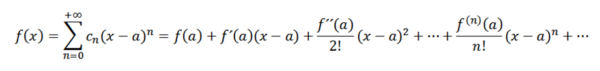
Te serie są znane jako Taylor F w serii. Kiedy a = 0 mamy konkretny przypadek o nazwie Maclaurin Series. Ten typ serii ma ogromne znaczenie matematyczne, szczególnie w analizie numerycznej, ponieważ dzięki tym możemy zdefiniować funkcje w komputerach takich jak E^X , sin (x) i cos (x).

Przykład

Uzyskaj serię Maclaurin dla E^X.

Zauważ, że jeśli f (x) = e^X, Następnie f^(N)(x) = e^X i f^(N)(0) = 1, więc twoja seria Maclaurin to: