Pochodzące z obliczeń, demonstracji, ćwiczeń

Kotangent pochodzący Jest równy przeciwnikowi kwadratu zbiorów „-CSC²". Ta formuła wynika z praw pochodnych z definicji i różnicowania funkcji trygonometrycznych. Jest to oznaczone w następujący sposób:

D (CTG u) = -CSc² Lub . du

Gdzie „du” symbolizuje wyrażenie pochodzące z funkcji argumentu, w odniesieniu do zmiennej niezależnej.

Źródło: Pixabay.com

[TOC]

Jak to jest obliczane?

Procedura opracowywania tych pochodnych jest dość prosta. Po prostu zidentyfikuj argument i rodzaj reprezentowanej funkcji.

Na przykład wyrażenie CTG (f/g) przedstawia podział w swoim argumencie. Będzie to wymagało różnicowania w odniesieniu do U/V, po opracowaniu ZIP.

Cotangent to wzajemna funkcja stycznej. Algebraicznie oznacza to, że:

(1/tg x) = CTG x

CTG x = cos x / sen x

Nieprawidłowe jest stwierdzenie, że funkcja Cotangent jest „odwrotnością” stycznej. Wynika to z faktu, że odwrotna funkcja stycznej z definicji to łuk styczny.

(TG^-1 x) = arctg x

Według trygonometrii pytagorejskiej Cotangent jest zaangażowany w następujące sekcje:

CTG x = (cos x) / (sin x)

CTG² X + 1 = csc² X

Według trygonometrii analitycznej odpowiada na następujące tożsamość:

CTG (a + b) = (1 - tg a . Tg b) / (tg a + tg b)

CTG (a - b) = (1 + tg a . Tg b) / (tg a - tg b)

CTG (2a) = (1 - tg² a) / (2tg a)

Charakterystyka funkcji Cotangent

Konieczne jest przeanalizowanie różnych cech funkcji F (x) = CTG X, aby móc zdefiniować niezbędne aspekty w celu zbadania jego zróżnicowania i zastosowania.

Asymptoty pionowe

Funkcja Cotangent nie jest zdefiniowana w wartościach, które sprawiają, że wyrażenie „Senx” zero. Ze względu na jego równoważne CTG x = (cos x) / (sin x), będzie miał nieokreśloność we wszystkich „nπ” z n należącym do liczb całkowitych.

Może ci służyć: geometria analityczna

To znaczy, w każdej z tych wartości x = nπ, będzie asymptotek pionowy. Gdy zbliża się wartość Cotangent, a przy zbliżaniu się do prawej funkcja wzrośnie w nieskończoność.

Domena

Domena funkcji Cotangent jest wyrażona przez zestaw x ∈ R / x ≠ nπ, n ∈ Z. Jest to odczytywane jako „x, które należy do zestawu liczb rzeczywistych, tak że x różni się od nπ, przy czym N należą do całej liczby”.

Zakres

Ranga funkcji Cotangent obejmuje mniej do bardziej nieskończoności. Dlatego można stwierdzić, że jego ranga jest zbiorem rzeczywistych liczb n.

Częstotliwość

Funkcja Cotangent jest okresowa, a jej okres jest równy π. W ten sposób równość ctg x = ctg (x + nπ) jest wypełniona, gdzie n należy do z z.

Zachowanie

Jest to dziwna funkcja, ponieważ CTG (-x) = - CTG x. W ten sposób wiadomo, że funkcja przedstawia symetrię w odniesieniu do pochodzenia współrzędnych. Przedstawia również spadek w każdym przedziale położonym między 2 kolejnymi pionowymi asymptotami.

Nie ma wartości maksymalnych ani minimalnych, ponieważ ich podejścia do pionowych asymptotów mają zachowania, w których funkcja rośnie lub zmniejsza się w nieskończoność.

Zero lub korzenie funkcji Cotangent znajdują się w nieparzystych wielokrotnościach π/2. Oznacza to, że CTG x = 0 jest spełnione w wartościach postaci x = nπ/2 z całością.

Demonstracja

Istnieją 2 sposoby wykazania pochodnej funkcji Cotangent.

Trygonometryczna demonstracja różnicowa

Pochodna funkcji kotangentu została wykazana na podstawie jej równoważnej w piersi i konsenosach.

Może ci służyć: algebra boolean: historia, twierdzenia i postulaty, przykłady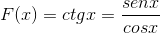

Chodzi o pochodną podziału funkcji

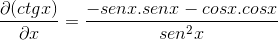
Po wyprowadzeniu czynników są pogrupowane i tożsamości pitagorejskie mają na celu naśladowanie

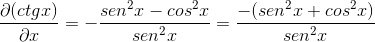
Zastąpienie tożsamości i stosowanie wzajemności Uzyskuje się wyrażenie

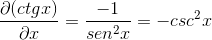
Definicja definicji pochodnej

Poniższe wyrażenie odpowiada z definicji pochodnej. Gdzie odległość między 2 punktami funkcji zbliża się zero.

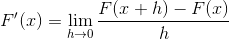
Zastępując Cotangente, musisz:

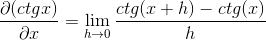
Tożsamości mają zastosowanie do sumy argumentów i wzajemności

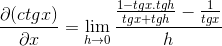
Ułamek licznika jest tradycyjnie obsługiwany

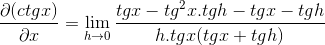
Uzyskane jest eliminowanie przeciwnych elementów i rysowanie wspólnego czynnika

Stosowanie tożsamości i wzajemności pitagorejskiej

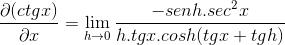
Elementy ocenione w x są stałe w odniesieniu do granicy, dlatego mogą pozostawić argument tego. Następnie stosowane są limity trygonometryczne.

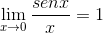
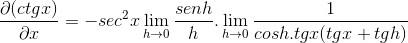
Limit jest oceniany

Następnie uwzględnia się, aż osiągnie pożądaną wartość

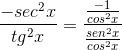
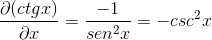
Jest to wykazane przez pochodną Cotangente jako przeciwieństwo kwadratu kombajsu.

Rozwiązane ćwiczenia

Ćwiczenie 1

Zgodnie z funkcją f (x) zdefiniuj wyrażenie f '(x)

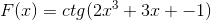
Odpowiednie wyprowadzenie jest stosowane w zakresie reguły łańcucha

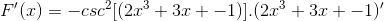
Wyprowadzenie argumentu

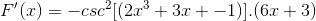
Czasami konieczne jest zastosowanie tożsamości wzajemnej lub trygonometrycznej w celu dostosowania rozwiązań.

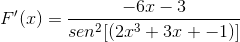
Ćwiczenie 2

Zdefiniuj ekspresję różnicową odpowiadającą F (x)

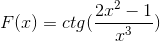
Zgodnie z wzorem wyprowadzania i poszanowaniem zasady łańcucha

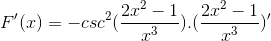
Argument jest wyprowadzony, a reszta pozostaje taka sama

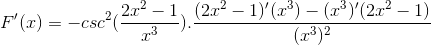
Wyprowadzanie wszystkich elementów

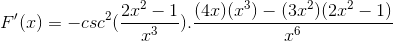
Działający w tradycyjny sposób produkty tej samej bazy

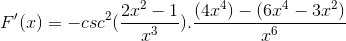
Dodano te same elementy i wyodrębnia się wspólny czynnik

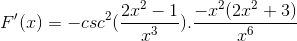
Znaki są uproszczone i obsługiwane. Ustalenie miejsca całkowicie wyprowadzonym wyrażeniu

Może ci służyć: różnica między wspólną frakcją a liczbą dziesiętną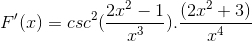

Bibliografia

1. Seria trygonometryczna, tom 1. DO. Zygmund. Cambridge University Press, 2002
2. Rachunek pojedynczej zmiennej. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 listopada. 2008
3. Rachunek z trygonometrią i geometrią analityczną. John H. Saxon, John Saxon, Frank Wang, Diana Harvey. Saxon Publishers, 1988
4. Analiza wielowymiarowa. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 grudnia. 2010
5. Dynamika systemu: modelowanie, symulacja i kontrola systemów mechatronicznych. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 marca. 2012
6. Rachunek: matematyka i modelowanie. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 stycznia. 1999