Stałe znaczenie, obliczenia i przykłady integracji

Stała integracji Jest to wartość dodana do obliczania antiderivative lub całek, służy do reprezentowania rozwiązań, które składają się na prymitywne funkcje. Wyraża nieodłączną dwuznaczność, w której każda funkcja ma nieskończoną liczbę prymitywnych.

Na przykład, jeśli funkcja jest przyjmowana: f (x) = 2x + 1 i otrzymujemy jej antyderowative:

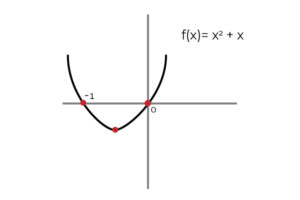
∫ (2x+1) dx = x² + X + C ; Gdzie C To jest Stała integracji i graficznie reprezentuje pionowe tłumaczenie między nieskończonymi możliwościami prymitywnych. Prawidłowo to powiedzieć (x² + x) Jest A prymitywnego f (x).

Źródło: Autor

W ten sam sposób możesz zdefiniować (x² + X + C ) jako prymityw F (x).

[TOC]

Odwrotna właściwość

Można zauważyć, że po wyprowadzeniu wyrażenia (x² + x) Otrzymuje się funkcję f (x) = 2x + 1. Wynika to z odwrotnej właściwości między wyprowadzeniem a integracją funkcji. Ta właściwość pozwala uzyskać formuły integracji, zaczynając od różnicowania. Co umożliwia weryfikację całek przez te same pochodne.

Źródło: Autor

Jednak (x² + x) Nie jest to jedyna funkcja, której pochodna jest równa (2x + 1).

1. D (X² + x)/ dx = 2x + 1
2. D (X² + x + 1)/ dx = 2x + 1
3. D (X² + x + 2)/ dx = 2x + 1
4. D (X² + x + 3)/ dx = 2x + 1
5. D (X² + X + C)/ dx = 2x + 1

Gdzie 1, 2, 3 i 4 reprezentują szczególny prymitywny F (x) = 2x + 1. Podczas gdy 5 reprezentuje nieokreśloną lub prymitywną całkę F (x) = 2x + 1.

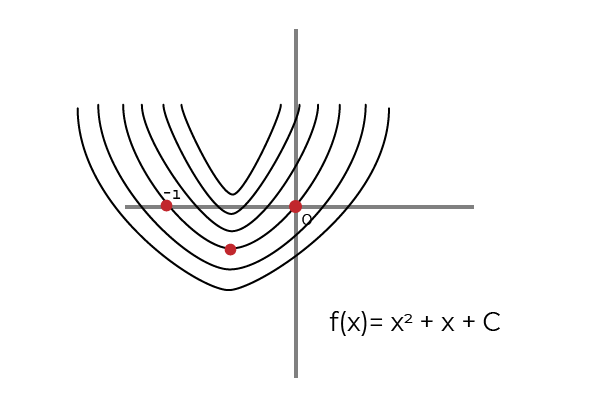Źródło: Autor

Prymitywne funkcje są osiągane poprzez proces antyderywacyjny lub integralny. Gdzie f będzie prymitywnym F, jeśli następujące są spełnione

• y = ∫ f (x) dx = F (x) + c; C = Stała integracji
• F '(x) = f (x)

Doceniamy, że funkcja ma jedną pochodną, ​​w przeciwieństwie do jej nieskończonej prymitywnej wynikającej z integracji.

Całka nieokreślona

 ∫ f (x) dx = f (x) + c

Odpowiada rodzinie krzywych o tym samym wzorze, który doświadcza niezgodności w wartości obrazów każdego punktu (x, y). Każda funkcja, która spełnia ten wzór, będzie indywidualny prymitywny, a zestaw wszystkich funkcji jest znany jako Integral nieokreślony.

Wartość Stała integracji Będzie to ten, który różnicuje każdą funkcję w praktyce.

Stała integracji Sugeruje pionowe przemieszczenie na wszystkich wykresach reprezentujących prymitywne funkcję. Gdzie obserwuje się między nimi równoległość i fakt, że C Jest to wartość przemieszczenia.

Według powszechnych praktyk Stała integracji Jest to oznaczone literą „c” po dodaniu, chociaż w praktyce jest obojętne, jeśli stała dodaje lub odejmuje. Jego rzeczywistą wartość można znaleźć na różne sposoby według różnych warunki początkowe.

Inne znaczenia stałej integracji

Mówiono już o tym, jak Stała integracji jest stosowany w gałęzi Rachunek integralny; Reprezentując rodzinę krzywych, które definiują nieokreśloną całkę. Ale wiele innych nauk i gałęzi przypisało bardzo interesujące i praktyczne wartości Stała integracji, którzy ułatwili rozwój wielu badań.

Może ci służyć: prostokątne trapez: właściwości, relacje i wzory, przykłady

w fizyczny Stała integracji może przyjmować wiele wartości zgodnie z charakterem danych. Bardzo powszechnym przykładem jest znanie funkcji V (t) który reprezentuje prędkość cząstki w porównaniu z czasem t. Wiadomo, że przy obliczaniu prymitywnego v (t) uzyskiwana jest funkcja R (t) który reprezentuje pozycja cząstki w porównaniu z czasem.

Stała integracji będzie reprezentować wartość początkowej pozycji, to znaczy w tej chwili t = 0.

Podobnie, jeśli funkcja jest znana NA)  który reprezentuje przyśpieszenie cząstki w porównaniu z czasem. Prymityw A (t) spowoduje funkcję v (t), gdzie Stała integracji Będzie to wartość początkowej prędkości v₀.

w gospodarka, Uzyskując prymityw funkcji kosztów przez integrację. Stała integracji będzie reprezentować koszty stałe. I wiele innych aplikacji, które zasługują na różnicowy i integralny rachunek.

Jak obliczana jest stała integracja?

Do obliczenia Stała integracji, Zawsze będzie konieczne poznać warunki początkowe. Które są odpowiedzialne za zdefiniowanie, który z możliwych prymitywnych jest odpowiedni.

W wielu aplikacjach jest traktowany jako zmienna niezależna do czasu (t), gdzie stała C Weź wartości, które definiują warunki początkowe konkretnego przypadku.

Jeśli pobrany jest początkowy przykład: ∫ (2x+1) dx = x² + X + C

Prawidłowym warunkiem początkowym może być warunek grafiki w celu przejścia przez określoną współrzędną. Na przykład wiadomo, że prymitywne (x² + X + C) Przejdź przez punkt (1, 2)

F (x) = x² + X + C; To jest ogólne rozwiązanie

F (1) = 2

W tej równości zastępujemy ogólne rozwiązanie

F (1) = (1)² + (1) + c = 2

Gdzie można go łatwo wywnioskować C = 0

W ten sposób odpowiednią prymitywem w tej sprawie jest F (x) = x² + X

Istnieją różne rodzaje ćwiczeń numerycznych, które działają Stałe integracyjne. W rzeczywistości rachunek różnicowy i integralny nie przestaje być stosowany w bieżących badaniach. Na różnych poziomach akademickich można znaleźć; Od wstępnych obliczeń, poprzez fizykę, chemię, biologię, gospodarkę,.

Jest to również doceniane w badaniu równania różniczkowe, gdzie Stała integracji Możesz przyjmować różne wartości i rozwiązania, to ze względu na wiele skierowań i integracji przeprowadzanych w tej sprawie.

Przykłady

Przykład 1

1. Działo położone 30 metrów wysokości pędu pionowo po pocisku. Wiadomo, że początkowa prędkość pocisku wynosi 25 m/s. Określić:

• Funkcja, która określa pozycję pocisku w odniesieniu do czasu.
• Czas lub czas lotu, w którym cząstka gra na ziemi.

Może ci służyć: 8 rodzajów błędów pomiarowych (z przykładami)

Wiadomo, że w równomiernie zróżnicowanym przyspieszenie ruchu prostoliniowego jest stałą wartością. Tak jest w przypadku uruchomienia pocisku, w którym przyspieszenie będzie grawitacją

G = - 10 m/s²

Wiadomo również, że przyspieszenie jest drugim pochodzącym z pozycji, co wskazuje na podwójną integrację z rozdzielczością ćwiczenia, uzyskując w ten sposób dwa Stałe integracyjne.

A (t) = -10

V (t) = ∫a (t) dt = ∫ (-10t) dt = -10t + C₁

Początkowe warunki ćwiczenia wskazują, że prędkość początkowa to v₀ = 25 m/s. To jest prędkość w czasie t = 0. W ten sposób się spełnia, że:

V (0) = 25 = -10 (0) + C₁   I C₁ = 25

Definiowana funkcja prędkości

V (t) = -10t + 25; Możesz zobaczyć podobieństwo do formuły MRUV (v_F = V₀ + A x t)

W homologicznym funkcja prędkości jest zintegrowana w celu osiągnięcia wyrażenia, które określa pozycję:

R (t) = ∫v (t) dt = ∫ (-10t+25) dt = -5t² + 25t + C₂

R (t) = -5t² + 25t + C₂  (Pozycja prymitywna)

Położenie początkowe r (0) = 30 m jest znane. Wówczas obliczany jest konkretny prymitywny pocisk.

R (0) = 30m = -5 (0)² + 25 (0) + C₂ . Gdzie C₂ = 30

Pierwsza sekcja jest rozwiązana od tego czasu R (t) = -5t² + 25t + 30  ; To wyrażenie jest homologiczne w stosunku do wzoru przemieszczenia w mruv r (t) = r₀ + V₀T - gt²/2

W drugiej sekcji należy rozwiązać równanie kwadratowe: -5t² + 25t + 30 = 0

Ponieważ warunki cząsteczki dotarły do ​​ziemi (pozycja = 0)

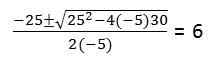Źródło: Autor

Właściwie równanie drugiej klasy rzuca 2 rozwiązania T: 6, -1. Wartość t = -1 jest ignorowana, ponieważ są to jednostki czasu, których domena nie zawiera liczb ujemnych.

W ten sposób rozstrzygana jest druga sekcja, w której czas lotu jest równy 6 sekund.

Przykład 2

2. Znajdź prymitywne f (x), które spełniają początkowe warunki:

• f "(x) = 4; f '(2) = 2; f (0) = 7

Z informacją o drugiej pochodnej F "(x) = 4 rozpoczyna

f '(x) = ∫f "(x) dx

∫4 dx = 4x + c₁

Następnie znajomość stanu f '(2) = 2 przebiega:

4 (2) + C₁ = 2

C₁ = -6 i f '(x) = 4x - 8

Kontynuuj w ten sam sposób na sekundę Stała integracji

f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2x² - 8x + c₂

Warunek początkowy f (0) = 7 jest znany i kontynuuj:

2 (0)² - 8 (0) + c₂ = 7

C₂ = 7 i f (x) = 2x² - 8x + 7

• f "(x) = x² ; f '(0) = 6; f (0) = 3

Podobne do poprzedniego problemu definiujemy pierwsze pochodne i pierwotną funkcję z początkowych warunków.

f '(x) = ∫f "(x) dx

∫ (x²) Dx = (x³/3) + C₁

Ze stanem f '(0) = 6 postępuje:

Może ci służyć: SET Teoria: Charakterystyka, elementy, przykłady, ćwiczenia

(0³/3) + C₁ = 6; Gdzie₁ = 6 i f '(x) = (x³/3) + 6

Potem drugi Stała integracji

f (x) = ∫f '(x) dx

∫ [(x³/3) + 6] dx = (x⁴/12) + 6x + c₂

Warunek początkowy f (0) = 3 jest znany i postępuj:

[(0)⁴/12] + 6 (0) + C₂ = 3; Gdzie₂ = 3

Otrzymuje się konkretne prymitywne

f (x) = (X⁴/12) + 6x + 3

Przykład 3

3. Zdefiniuj funkcje prymitywne, biorąc pod uwagę pochodne i punkt wykresu:

• dy/dx = 2x - 2, który przechodzi przez punkt (3, 2)

Ważne jest, aby pamiętać, że pochodne odnoszą się do nachylenia stycznej linii do krzywej w pewnym momencie. Gdzie nie jest prawidłowe założenie, że grafika pochodnej dotyka wskazanego punktu, ponieważ należy do wykresu funkcji prymitywnej.

W ten sposób wyrażamy równanie różniczkowe w następujący sposób:

dy = (2x - 2) dx  ; Następnie stosując kryteria antideriwacyjne:

∫DY = ∫ (2x - 2) dx

y = x² - 2x + c

Zastosowanie warunków początkowych:

2 = (3)² - 2 (3) + C

C = -1

Otrzymuje: f (x) = x² - 2x - 1

• dy/dx = 3x² - 1, który przechodzi przez punkt (0, 2)

Wyrażamy równanie różniczkowe w następujący sposób:

dy = (3x² - 1) DX  ; Następnie stosując kryteria antideriwacyjne:

 ∫DY = ∫ (3x² - 1) DX

y = x³ - x + c

Zastosowanie warunków początkowych:

2 = (0)² - 2 (0) + c

C = 2

Otrzymuje: f (x) = x³ - x + 2

Proponowane ćwiczenia

Ćwiczenie 1

1. Znajdź prymitywne f (x), które spełniają początkowe warunki:

• f "(x) = x; f '(3) = 1; f (2) = 5
• f "(x) = x + 1; f '(2) = 2; f (0) = 1
• f "(x) = 1; f '(2) = 3; f (1) = 10
• f "(x) = -x; f '(5) = 1; f (1) = -8

Ćwiczenie 2

2. Balon, który wznosi się z prędkością 16 stóp/s uwalnia płaszcz z piasku z wysokości 64 stóp nad poziomem gruntu.

• Zdefiniuj czas lotu
• Jaki będzie wektor v_F Kiedy dotykasz podłogi?

Ćwiczenie 3

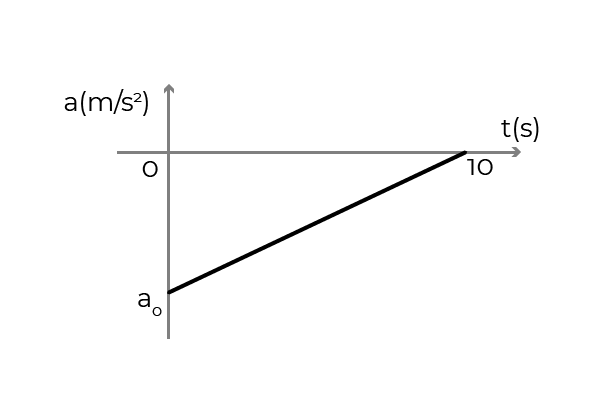
3. Rysunek pokazuje wykres przyspieszenia - czas samochodu, który porusza się w pozytywnym sensie osi x. Samochód jechał do stałej prędkości 54 km/h, gdy kierowca nałożył hamulce, aby zatrzymać się w 10 sekund. Określić:

• Początkowe przyspieszenie samochodu
• Prędkość samochodu przy t = 5s
• Przemieszczenie samochodu podczas hamowania

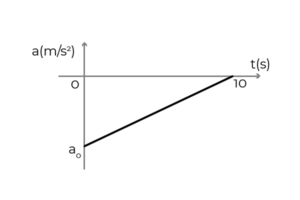Źródło: Autor

Ćwiczenie 4

4. Zdefiniuj funkcje prymitywne, biorąc pod uwagę pochodne i punkt wykresu:

• dy/dx = x, który przechodzi przez punkt (-1, 4)
• dy/dx = -x² + 1, który przechodzi przez punkt (0, 0)
• dy/dx = -x + 1, który przechodzi przez punkt (-2, 2)

Bibliografia

1. Rachunek integralny. Nieokreślone metody integracji i integracji. Wilson, Velásquez Bastidas. Magdalena 2014 University
2. Stewart, J. (2001). Obliczanie zmiennej. Wczesny transcendent. Meksyk: Thomson Learning.
3. Jiménez, r. (2011). Matematyka VI. Rachunek integralny. Meksyk: Pearson Education.
4. Fizyka i. MC Graw Hill