Ściśniowość ciał stałych, cieczy, gazów, przykładów

ściśliwość substancji lub materiału jest zmiana objętości, której doświadcza, gdy podlega zmianie ciśnienia. Zwykle objętość zmniejsza się podczas wywierania nacisku na system lub obiekt. Czasami występuje odwrotnie: zmiana ciśnienia może wywołać eksplozję, w której system zwiększa objętość lub gdy nastąpi zmiana fazowa.

W niektórych reakcjach chemicznych może się to zdarzyć, a także w gazach, ponieważ zwiększając częstotliwość kolizji, zachodzą siły odpychające.

Podwodne doświadcza sił kompresji po zanurzeniu. Źródło: Pixabay.com.

Wyobrażając sobie, jak łatwe lub trudne może być kompresowanie obiektu, musisz rozważyć trzy stany, w których materia jest normalnie: stała, ciekła i gazowa. W każdym z nich cząsteczki utrzymują od siebie pewne odległości. Im bardziej twarde łącza łączące cząsteczki substancji, które składają się na obiekt i bliżej, tym trudniejsze będzie spowodowanie deformacji.

Solidność ma swoje bardzo bliskie cząsteczki, a gdy próbują więcej, pojawiają się siły odpychania, które utrudniają zadanie. Dlatego mówi się, że substancje stałe są nieczyste. W cząsteczkach ciekłych jest więcej miejsca, więc jego ściśliwość jest większa, ale zmiana objętości zwykle wymaga dużych sił.

Więc ciśnie stałe i ciecze nie są ściśliwe. Konieczna byłaby bardzo duża zmiana ciśnienia, aby osiągnąć znaczącą zmianę w warunkach normalnego ciśnienia i temperatury SO. Z drugiej strony gazy, ponieważ mają bardzo rozmieszczone cząsteczki, są łatwo ściskane i dekompresowane.

[TOC]

Solidność ściśliwości

Gdy obiekt jest zanurzony na przykład w płynie, wywiera ciśnienie na obiekt we wszystkich kierunkach. W ten sposób możemy myśleć, że objętość obiektu zmniejszy się, chociaż w większości przypadków nie będzie to znaczące.

Sytuacja można zobaczyć na poniższym rysunku:

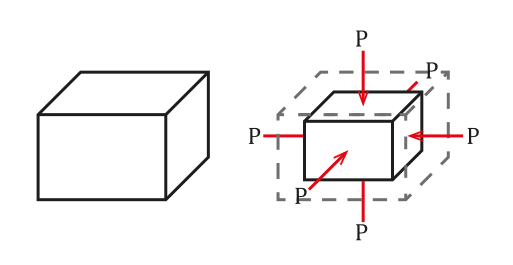Siła wywierana przez płyn na zanurzony obiekt jest prostopadle do powierzchni. Źródło: Wikimedia Commons.

Ciśnienie jest definiowane jako siła na jednostkę powierzchni, co spowoduje zmianę objętości δv proporcjonalną do początkowej objętości obiektu v_albo. Ta zmiana objętości będzie zależeć od tych samych cech.

Prawo Hooke stwierdza, że ​​odkształcenie doświadczane przez obiekt jest proporcjonalne do wysiłku stosowanego w nim:

Wysiłek ∝ Deformacja

Odkształcenie objętościowe doświadczane przez ciało jest określone ilościowo przez B wymaganą stałą proporcjonalności, która jest nazywana jako moduł objętościowy materiału:

B = -Sft/Jednolitowe odkształcenie

Może ci służyć: promieniowanie termiczne: właściwości, przykłady, aplikacje

B = -pp/ (δv/ v_albo)

Jak δv/v_albo Jest to ilość bezwymiarowa, ponieważ jest to iloraz między dwoma objętościami, moduł objętościowy ma te same jednostki ciśnieniowe, które w systemie międzynarodowym są Pascal (PA).

Znak ujemny wskazuje oczekiwane zmniejszenie objętości, gdy obiekt jest wystarczająco ściśnięty, to znaczy ciśnienie wzrasta.

-Ściśliwość materiału

Odwrotna lub wzajemna wartość modułu objętościowego jest znana jako ściśliwość I jest oznaczony tekstami k. Dlatego:

Tutaj k Jest to ujemna zmiana objętości ułamkowej spowodowana wzrostem ciśnienia. Jego jednostki w systemie międzynarodowym są odwrotność PA, to znaczy m² /N.

Równanie dla B lub K, jeśli są preferowane, ma zastosowanie zarówno do stałych, jak i cieczy. Koncepcja modułu objętościowego jest rzadko stosowana do gazów. Później wyjaśniono prosty model, aby określić ilościowo spadek objętości, którego może doświadczyć prawdziwy gaz.

Prędkość dźwięku i moduł ściśliwości

Interesującą aplikacją jest prędkość dźwięku w medium, który zależy od modułu ściśliwości tego samego:

Gdzie C jest prędkością dźwięku, B jest modułem objętościowym, a ρ jest gęstością medium

Rozwiązane ćwiczenia-podejście

-Ćwiczenie rozwiązane 1

Solidna mosiężna kula, której objętość wynosi 0.8 m³ Spada do oceanu na głębokość, na której ciśnienie hydrostatyczne jest o 20 m większe niż na powierzchni. Jaka zmiana doświadczy objętości sfery? Wiadomo, że mosiężna moduł ściśliwości jest B = 35 000 MPa,

Rozwiązanie

1 M PA = 1 Mega Pascal = 1. 10 ⁶ Rocznie

Zmiana ciśnienia w odniesieniu do powierzchni wynosi DP = 20 x 10 ⁶ Rocznie. Stosując podane równanie dla B, masz:

B = -pp/ (δv/ v_albo)

Dlatego:

Więc:

Δv = -5.71.10 ^-4 x 0.8 m³ = -4.57 x 10^-4 M³

Różnica głośności może mieć znak ujemny, gdy ostateczny objętość jest mniejsza niż początkowa objętość, dlatego wynik ten zgadza.

Moduł ściśliwości tak wysoki wskazuje, że wymagana jest duża zmiana ciśnienia, aby obiekt doświadczył znacznego zmniejszenia objętości.

-Ćwiczenie rozwiązane 2

Uchanie ucha na torach kolejowych jest znane, gdy w oddali zbliża się jeden z tych pojazdów. Jak długo trwa dźwięk podczas podróży przez stalową szynę, jeśli pociąg znajduje się 1 km?

Może ci służyć: ochrona pędu liniowego: zasada, przykłady, ćwiczenia.

Dane

Gęstość stali = 7.8 x 10 ³ kg/m3

Moduł ściśliwości stalowej = 2.0 x 10 ^jedenaście Rocznie.

Rozwiązanie

Ściśniowość płynów

Moduł ściśliwości B obliczony powyżej jest również stosowany do płynów, chociaż zwykle wymagany jest duży wysiłek w celu uzyskania znacznego spadku objętości. Ale płyny mogą się rozwijać lub kurczyć się w miarę ogrzewania lub chłodzenia, a także jeśli są zniechęcone lub podciśnięte.

W przypadku wody w warunkach standardowych ciśnienia i temperatury (0 ° C i atmosfera ciśnieniowa około lub 100 kPa) moduł objętości. To znaczy około 21000 razy ciśnienie atmosferyczne.

Dlatego w większości zastosowań ciecze są zwykle uważane za nieporadne. Można to natychmiast zobaczyć w aplikacji numerycznej.

-Ćwiczenie rozwiązane 3

Znajdź ułamkowy spadek objętości wody, gdy poddano ciśnieniu 15 MPa.

Rozwiązanie

Ściśniowość w gazach

Gazy, jak wyjaśniono powyżej, działają nieco inaczej.

Wiedzieć, jaki mają tom N mole danego gazu, gdy jest on ograniczony pod ciśnieniem P i w temperaturze T, Stosowane jest równanie stanu. W równaniu stanu dla gazu idealnego, w którym siły międzycząsteczkowe nie są brane pod uwagę, najprostszy model wskazuje, że:

P.V_ideał = n. R. T

Gdzie r jest stałą gazów idealnych.

Zmiany objętości gazu można przeprowadzić przy stałym ciśnieniu lub w stałej temperaturze. Na przykład, utrzymując stałą temperatury, ściśliwość izotermiczna κ_T Jest:

Zamiast symbolu „delta”, który został użyty przed zdefiniowaniem koncepcji ciał stałych, dla gazu jest opisywany z pochodną, ​​w tym przypadku częściowe wyprowadzone w odniesieniu do p, utrzymując stałą t.

Dlatego B_T Izotermiczny moduł ściśliwości to:

 B_T = p

A także ważny jest również adiabatyczny moduł kompresji Bu_Adiabatyczne, Dla których nie ma przychodzącego ani wychodzącego przepływu ciepła.

B_Adiabatyczne = γP

Gdzie γ jest współczynnikiem adiabatycznym. Przy tym współczynniku możesz obliczyć prędkość dźwięku w powietrzu:

-Ćwiczenie rozwiązane 4

Stosując poprzednie równanie, znajdź prędkość dźwięku w powietrzu.

Dane

Adiabatyczny moduł ściśliwości powietrza wynosi 1,42 × 10⁵ Rocznie

Gęstość powietrza wynosi 1.225 kg/m³ (pod ciśnieniem atmosferycznym i 15 ° C)

Rozwiązanie

Współczynnik ściśliwości z

Zamiast pracować z modułem ściśliwości, jako jednostka zmiana objętości z powodu zmiany ciśnienia, Realny współczynnik ściśliwości gazu, Inna, ale ilustracyjna koncepcja na temat tego, jak prawdziwy gaz porównuje się z idealnym gazem:

Może ci służyć: pofalowana teoria światła: wyjaśnienie, aplikacje, przykłady

P . V_prawdziwy = Z. R. T

Gdzie Z jest zgodnością ściśliwości gazu, która zależy od warunków, w których jest, będąc zwykle funkcją zarówno ciśnienia P, jak i temperatury, będąc w stanie wyrazić się jako:

Z = f (p, t)

W przypadku idealnego gazu z = 1. W przypadku prawdziwych gazów wartość Z prawie zawsze wzrasta wraz z ciśnieniem i zmniejsza się wraz z temperaturą.

Zwiększając ciśnienie, cząsteczki gazowe zderzają się częściej, a siły odpychające między nimi są zwiększone. Może to prowadzić do wzrostu objętości w prawdziwym gazie, więc Z> 1.

Z drugiej strony, do niższych ciśnień, cząsteczki mogą się swobodnie poruszać, a siły przyciągania dominują. W tym przypadku z < 1.

Dla prostego przypadku 1 molowego gazu n = 1, jeśli zachowane są te same warunki ciśnienia i temperatury, poprzez podzielenie terminu uzyskane są poprzednie równania:

Stwierdzono, że:

V_prawdziwy = Z v_ideał

-Ćwiczenie rozwiązane 5

Istnieje prawdziwy gaz na poziomie 250 ° K i 15 atm ciśnienia, który ma objętość molową o 12 % niższą niż obliczona według stanu gazów idealnych. Jeśli ciśnienie i temperatura pozostają stałe, znajdź:

a) współczynnik ściśliwości.

b) objętość molowa prawdziwego gazu.

c) jakie rodzaje sił dominują: atrakcyjny lub odpychający?

Rozwiązanie

a) Jeśli rzeczywistą objętość jest o 12 % niższa niż idealna, oznacza to, że:

V_prawdziwy = 0.88 v_ideał

Dlatego dla 1 mol gazu współczynnik ściśliwości to:

Z = 0.88

b) Wybór stałej gazów idealnych z odpowiednimi jednostkami dla dostarczonych danych:

R = 0,082 l.ATM/MOL.K

Objętość molowa jest obliczana przez wyczyszczenie i zastępowanie wartości:

c) dominują siły atrakcyjne, ponieważ z jest mniejsze niż 1.

Bibliografia

1. Atkins, str. 2008. Chemia fizyczna. Pan -american Medical Redaktorial. 10 - 15.
2. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6^th. Ed Prentice Hall. 242 - 243 i 314-15
3. Mott, r.  2006. Mechanika płynów. Edukacja Pearsona.13-14.
4. Rex, a. 2011. Podstawy fizyki. Edukacja Pearsona. 242-243.
5. Tipler, str. (2006) Physics for Science and Technology. Ed. Tom 1. Redakcja Reverted. 542.