Klasyfikacja liczb rzeczywistych

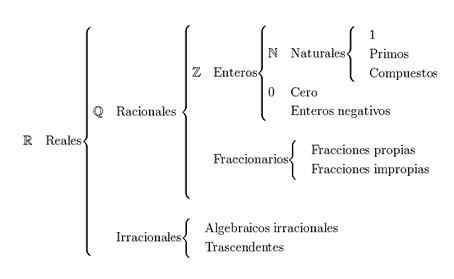
Główny Klasyfikacja liczb rzeczywistych Jest podzielony na liczby naturalne, liczby całkowitą, liczby racjonalne i liczby irracjonalne. Liczby rzeczywiste są reprezentowane z literą r.

Liczby rzeczywiste odnoszą się do kombinacji racjonalnych i irracjonalnych grup liczb. Aby utworzyć te grupy, potrzebne są liczby naturalne i liczby całkowite.

Istnieje wiele sposobów budowania lub opisania różnych liczb rzeczywistych, od prostszych form do bardziej złożonych form, w zależności od pracy matematycznej, którą chcesz wykonać.

Jak klasyfikowane są liczby rzeczywiste?

- Liczby naturalne

Liczby naturalne są reprezentowane przez literę (n) i są używane do liczenia (0,1,2,3,4 ...). Na przykład „jest piętnaście Rosas w ogrodzie ”,„ populacja Meksyku pochodzi 126 miliony ludzi „lub” suma dwa I dwa Jest cztery". Należy zauważyć, że niektóre klasyfikacje obejmują 0 jako liczbę naturalną, a inne nie. 

Dwoje dzieci wykonujących sumę dwóch naturalnych liczb.

Naturalne liczby nie obejmują tych, które mają część dziesiętną. Dlatego „populacja Meksyku pochodzi 126.2 Miliony ludzi „lub” robi temperaturę 24.5 Nie można rozważyć naturalnych liczb Celsjusza ”.

W wspólnym języku, takich jak szkoły podstawowe, liczby naturalne można nazwać liczbami rachunkowymi, aby wykluczyć negatywne liczby całkowite i zero.

Liczby naturalne to podstawy, z którymi można zbudować wiele innych zestawów liczb: liczby całkowe, liczby racjonalne, liczby rzeczywiste i liczby złożone, między innymi.

Właściwości liczb naturalnych, takich jak podział i rozkład liczb podstawowych, są badane w teorii liczb. Problemy związane z liczeniem i porządkowaniem, takie jak wyliczenia i partycja, są badane w kombinatorycznym.

Mają kilka właściwości, takich jak: suma, mnożenie, odejmowanie, podział itp.

Może ci służyć: współczesna nauka

Numery porządkowe i kardynalne

Liczby naturalne mogą być porządkowe lub kardynał.

Liczby kardynalne byłyby te, które są używane jako liczby naturalne, jak wspomniano powyżej w przykładach. "Mieć dwa ciasteczka ”,„ Jestem ojcem trzy dzieci ”,„ pudełko zawiera dwa kremów z prezentów ". 

Orderałowie to te, które wyrażają porządek lub wskazują pozycję. Na przykład w wyścigu kolejność przybycia biegaczy jest wymieniona przez zwycięzcę i zakończenie ostatniego, który doszedł do mety.

W ten sposób zostanie powiedziane, że zwycięzcą jest „pierwszy”, następny „drugi”, następny „trzeci” i tak dalej do ostatniego. Liczby te mogą być reprezentowane przez list w prawym górnym rogu, aby uprościć pismo (1., 2., 3., 4 itd.).

- Liczby liczb całkowitych

Całe liczby składają się z tych naturalnych liczb i ich przeciwieństw, to znaczy liczb ujemny (0, 1, -1, 2, -2, 50, -50 ...). Podobnie jak liczby naturalne, nie obejmują one tych, którzy mają część dziesiętną.

Przykładem liczb całkowitych byłby „średnio 30. w Niemczech”, „Zatrzymałem się o 0 po osiągnięciu końca miesiąca”, „aby zejść do piwnicy, musisz zaznaczyć przycisk windy„ windy ”.

Z kolei liczby całkowitego nie można zapisać za pomocą komponentu ułamkowego. Na przykład liczby takie jak 8.58 lub √2 nie są liczbami całkowitymi.

Liczby całkowite są reprezentowane z literą (z). Z jest grupą zuboilu liczb racjonalnych Q, która z kolei tworzy grupę rzeczywistych liczb n. Podobnie jak liczby naturalne, Z jest nieskończoną grupą księgową.

Liczby całkowite stanowią najmniejszą grupę i najmniejszy zestaw liczb naturalnych. W teorii liczb algebraicznych liczby całkowite są czasami nazywane irracjonalnymi, aby odróżnić je od liczb całkowitych algebraicznych.

Może ci służyć: Projekt badawczy: strony, jak jest opracowany i przykład

- Liczby wymierne

Zestaw liczb wymiernych jest reprezentowany przez literę (q) i zawiera wszystkie te liczby, które można zapisać jako ułamek liczb całkowitych.

Oznacza to, że ten zestaw zawiera liczby naturalne (4/1), liczby całkowe (-4/1) i dokładne liczby dziesiętne (15,50 = 1550/100).

Rozkład 1/6 sera jest racjonalną liczbą.

Rozszerzenie dziesiętne liczby racjonalnej zawsze kończy się po skończonej liczbie cyfr (np. 15,50) lub gdy ta sama skończona sekwencja cyfr zaczyna się powtarzać wielokrotnie (np. 0,34566666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666. Dlatego w zestawie liczb wymiernych liczby są uwzględnione. czyste gazety lub mieszane gazety.

Dodatkowo każdy powtarzany lub końcowy dziesiętny reprezentuje liczbę racjonalną. Te stwierdzenia są prawdziwe nie tylko dla bazy 10, ale także dla dowolnego innego numeru podstawowego.

Realna liczba, która nie jest racjonalna, nazywa się irracjonal. Irracjonalne liczby obejmują na przykład √2, π i e. Ponieważ cały zestaw liczb racjonalnych jest zdrętwiały i że grupa liczb rzeczywistych nie jest zdrętwiała, można powiedzieć, że prawie wszystkie liczby rzeczywiste są irracjonalne.

Liczby racjonalne można formalnie zdefiniować jako klasy równoważności całych par (p, q), tak że q ≠ 0 lub równoważna zależność zdefiniowana przez (p1, q1) (p2, q2) tylko wtedy, gdy p1, q2 = p2q1.

Liczby racjonalne wraz z sumą i mnożeniem, tworzą pola, które składają się na całe liczby i są zawarte przez dowolną gałąź zawierającą całość.

- Irracjonalne liczby

Irracjonalne liczby to liczby rzeczywiste, które nie są liczbami racjonalnymi; Irracjonalne liczby nie można wyrazić jako ułamki. Liczby racjonalne to liczby złożone z ułamków liczb całkowitych.

W wyniku testu piosenkarza, który mówi, że wszystkie liczby rzeczywistych nie są nikczemne i że racjonalne, jeśli są liczbami, można stwierdzić, że prawie wszystkie liczby rzeczywiste są irracjonalne.

Może ci służyć: trajektoria i przemieszczenie

Gdy promień dwóch segmentów linii jest liczbą irracjonalną, można powiedzieć, że te segmenty linii są niezmierzone; co oznacza, że ​​nie ma wystarczającej długości, aby każda z nich mogła być „mierzona” z wieloma konkretnymi liczbą całkowitą tego samego.

Wśród liczb irracjonalnych są promień π okręgu do jego średnicy, liczba eulera (E), złotej liczby (φ) i pierwiastek kwadratowy dwóch; Co więcej, wszystkie korzenie kwadratowe liczby naturalnych są irracjonalne. Jedynym wyjątkiem od tej zasady są idealne kwadraty.

Można zaobserwować, że gdy liczby irracjonalne są wyrażone pozytywnie w układzie liczbowym (np. Liczby dziesiętne) nie kończą się ani nie powtarzają.

Oznacza to, że nie zawierają one sekwencji cyfr, powtórzenia, według którego dokonuje się linii reprezentacji.

Uproszczenie liczby irracjonalnej PI.

Na przykład: reprezentacja dziesiętna liczby π zaczyna się od 3.14159265358979, ale nie ma skończonej liczby cyfr, które mogą dokładnie reprezentować π, ani nie można ich powtórzyć.

Dowód, że dziesiętne rozszerzenie liczby racjonalnej musi zakończyć się lub powtórzyć, różni się od dowodu, że rozszerzenie dziesiętne musi być liczbą racjonalną; Chociaż podstawowe i nieco długie, testy te zajmują trochę pracy.

Zwykle matematycy na ogół nie przyjmują pojęcia „zakończenia lub powtarzania”, aby zdefiniować koncepcję racjonalnej liczby.

Irracjonalne liczby można również traktować za pomocą frakcji nieciągłych.

Bibliografia

1. Klasyfikuj liczby rzeczywiste. Wyzdrowiał z Chilimath.com.
2. Liczba naturalna. Wyzdrowiał z Wikipedii.org.
3. Klasyfikacja liczb. Ditutor wyzdrowiał.com.
4. Wyzdrowiał z Wikipedii.org.
5. Liczba niewymierna. Wyzdrowiał z Wikipedii.org.