Jest nazywany Znaczące liczby do ilości cyfr zawierających Mantisa liczby. Im więcej liczb ilość jest znana z największą precyzją. Przypominając, Mantisa jest liczbą, która towarzyszy moc 10, gdy liczba w notacji naukowej jest zapisywana.

Na przykład weźmy numer 0.00376, który jest napisany jako 3.76 x 10 ^-3. Mantisa ma 3.76, a liczba ma w sumie 3 znaczące liczby. Liczba 0.129 ma również 3 znaczące liczby, a 4.5 ma tylko 2.

Rysunek 1. Kalkulatory naukowe nigdy nie pokazują liczby znaczących liczb operacji. Źródło: Piqsels.

I co się stanie, gdy liczba jest całość? Oznacza to, że jest znany z wszelką możliwą precyzją, innymi słowy, ma nieskończoną precyzję. Na przykład, licząc ludzi, zwierzęta lub przedmioty, takie jak książki i telefony, wynik jest liczbą całkowitą i precyzyjną liczbą.

Jeśli powiemy, że w kinie jest 110 osób oglądających film, jest to dokładna liczba, ani więcej, ani mniej, i ma 3 znaczące postacie.

Znaczące liczby są obsługiwane przez niektóre proste zasady, które są zapamiętywane z niewielką praktyką, jak wtedy zobaczymy.

[TOC]

Zasady określenia znaczących liczb liczby

Zasada nr 1

Poprzednie zera nie liczą się jako znacząca liczba, więc 0.045 i 4.5 Mają oba 2 znaczące liczby, ponieważ zaczynają być liczone od lewej i zaczynają od pierwszej innej cyfry zerowej.

Zasada 2

Tylne zera (po prawej) do pierwszej znaczącej cyfry liczą się jako znacząca liczba (o ile jest to uzasadnione dokładnością przyrządu pomiarowego).

Wreszcie, zera, które są pośrodku, są również uznawane za znaczącą cyfrę.

Zasada 3

W przypadku liczb zapisanych w notacji naukowej wszystkie liczby Mantisy są znaczące, a wykładnik nie wpływa na precyzję.

Może ci służyć: średnia prędkość: wzory, jak jest obliczany i rozwiązany

Zasada 4

Gdy dokonują operacji z dziesiętną, na przykład poprzez obliczenie obszarów lub innych podobnych operacji, wynik musi mieć taką samą liczbę znaczących liczb jak ilość o najniższej liczbie znaczących liczb, które uczestniczyły w operacji. Ta reguła jest ważna dla każdej operacji arytmetycznej.

Zasada 5

Liczba liczby nie wpływa na jego liczbę znaczących liczb.

Od razu zobaczymy kilka przykładów tego i wszystkich innych zasad.

Przykłady

Przykład 1

Znajdź liczbę znaczących liczb w każdej z tych liczb.

a) 876

b) 1000.68

c) 0.00005026

d) 4.8

e) -6.99

Odpowiedzi

a) 876 ma 3 znaczące liczby.

b) 1000.68 ma 6 znaczących liczb, ponieważ zera w środkowej liczbie jako taka.

c) zamiast tego 0.00005026 ma 4 znaczące liczby. Zauważ, że 5 zer po lewej stronie 5 nie jest liczone jako znacząca liczba, zamiast 0 między 5 a 2 tak.

d) 4.8 ma 2 znaczące liczby.

e) -6.99 ma 3 znaczące liczby.

Przykład 2

Często podejmowanie środków, takich jak taśmy metryczne, zegarki, termometry, skale i tak dalej. Ile znaczących liczb powinniśmy zgłosić kwoty, które mierzymy w ten sposób?

Odpowiedź

Zależy to od uznania instrumentu, z którym jest mierzony. Załóżmy przykład: Zmierz zewnętrzną średnicę rurki, z ukończoną regułą i nr nernierem lub kingiem.

Nernie jest instrumentem, który bardzo dokładnie mierzy długości, ponieważ ma dodatkową małą skalę, zwaną noniusz, co pozwala na większą drobne, że tak powiem, gdy pomiar.

Jest to bardziej precyzyjne niż reguła stopniowana, ponieważ dzięki niej możemy nauczyć się bardziej znaczących postaci o określonej długości.

Dlatego nie ma sensu zgłaszać obwodu, powiedzmy, 35.88 cm, jeśli mierzymy to za pomocą pomiaru taśmy, ponieważ ten instrument nie jest wystarczająco precyzyjny, aby zgłosić tak wiele znaczących cyfr.

Może ci służyć: statyczne: historia, jakie badania, aplikacje, prawa

Uznanie a miary taśmowej jest podane przez:

Dla taśmy miary lub reguły milimetrowej A = 1 mm, czyli dziesiąta centymetra. Obwód zmierzony za pomocą taśmy pomiarowej należy zgłosić jako 35.9 cm.

Przykład 3

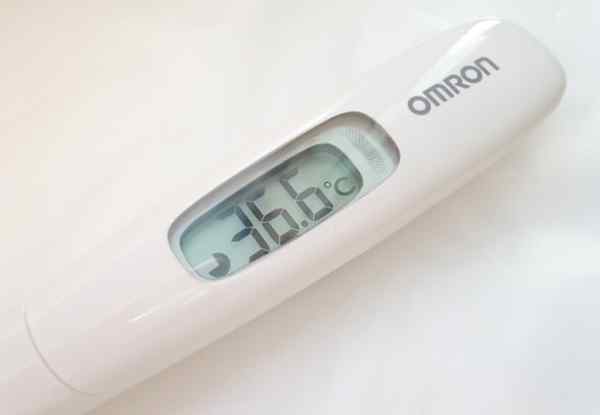
Ile znaczących liczb ma odczyt wykonany za pomocą termometru cyfrowego?

Odpowiedź

Termometr figury oferuje odczyty temperatury z trzema cyframi. Jednak do pokazanego zakresu 36.6 °.

Zwykłą rzeczą dla rodzaju pokazanego instrumentu cyfrowego jest błąd 0 uznania.1 ºC. To wystarczy, aby mieć pewność, że nie ma gorączki.

Rysunek 2. Cyfrowy termometr, którego odczyty są 3 istotnymi liczbami. Źródło: Pxhere.

Zasady okrągłych liczb

Gdy kalkulator jest używany do wykonywania obliczeń z uzyskanymi pomiarami, nie jest prawidłowe podanie wyniku za pomocą wszystkich cyfr, które pojawiają się na ekranie.

Tylko ci, którzy znają się dokładnie, są zachowani, ponieważ tylko te mają prawdziwe znaczenie. Następnie konieczne jest zaokrąglanie wyników, aby dopasować się do liczby znanych dokładnie cyfr. Te zasady to:

-Jeśli liczba, która następuje po cyfrze, która ma zostać zachowana równe lub większe niż 5, Do tej cyfry dodaje się 1.

Na przykład, zaokrąglając 3.786 Aby mieć dwa po przecinku, chcemy zachować liczby do 8. Ponieważ liczba, która następuje (6), jest większa niż 5, 8 staje się 8 + 1 = 9, a liczba pozostaje 3.79.

-Gdy liczba następująca po cyfrze, która ma zostać zachowana mniej niż 5, Cyfra jest taka sama.

Może ci służyć: Joule Efekt: Objaśnienie, przykłady, ćwiczenia, aplikacje

Jeśli chcemy runda 1.27924 Aby mieć tylko 3 dziesiętne, osiąga się to poprzez osiągnięcie 9, po którym następuje 2. Ponieważ 2 jest mniejsze niż 5, te dziesiętne znikają, a zaokrąglona liczba wynosi 1.279.

Ćwiczenie rozwiązane

Stół ma kształt i wymiary wskazane na przymocowanej figurze. Poproszono o obliczenie jego obszaru za pomocą reguł operacyjnych o znaczących liczbach.

Rozwiązanie

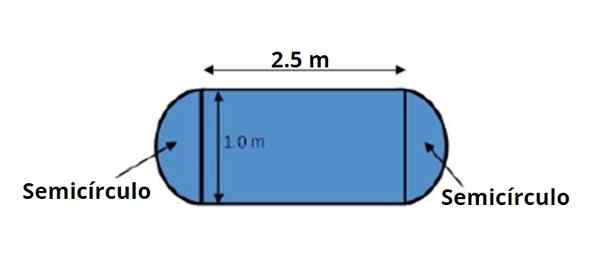Rysunek 3. Tabela ma kształt i wymiary wskazane na rysunku, zauważ, że są one znane z dwiema istotnymi postaciami. Źródło: f. Zapata.

Obszar stołu można podzielić na centralny prostokątny obszar i dwa półkole, po jednym z każdej strony, co razem tworzą 1 pełny okrąg.

Zadzwonimy₁ do obszaru prostokąta, podane przez:

DO₁ = podstawa × wysokość = 2.5 m x 1.0 m = 2.5m²

Ze swojej części obszar okręgu, który jest równoważny z 1 półkolem pomnożonym przez 2 to:

DO₂ = π × Radio²

Średnica jednego z półkoczek wynosi 1.0 m, dlatego promień wynosi 0.50 m. W tym przypadku średnicę można również wykorzystać bezpośrednio do obliczenia obszaru:

DO₂ = (π × średnica²) / 4

W każdym przypadku:

DO₂ = [π x (1.0 m)²] / 4 = 0.785398163 m²

Użyto wszystkich cyfr oferowanych przez kalkulator. Teraz dodajemy do₁ już₂ Dla całkowitego obszaru stołu:

A = (2.5 + 0.785398163) m² = 3.285398163 m²

Ponieważ wymiary tabeli są znane z 2 istotnymi liczbami, nie ma sensu wyrażać wyniku ze wszystkimi dziesiętnymi dziesiętnymi podawanymi przez kalkulator, co nigdy nie daje liczby znaczących liczb wyniku.

Trzeba zrobić, aby wokół obszaru, aby miał taką samą liczbę znaczących liczb jak wymiary tabeli, to znaczy 2. Dlatego końcowy wynik jest zgłaszany w ten sposób:

A = 3.3 m²

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
3. Fisicalab. Znaczące liczby i zaokrąglanie. Odzyskany z: fisicalab.com.
4. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.