Jednostkowe właściwości komórek, stała czerwona i typy

Jednolita komórka Jest to wyimaginowana przestrzeń lub region, który reprezentuje minimalny wyraz całości; Że w przypadku chemii całość byłaby kryształ złożony z atomów, jonów lub cząsteczek, które są uporządkowane zgodnie z wzorem strukturalnym.

W życiu codziennym można znaleźć przykłady, które ucieleśniają tę koncepcję. W tym celu należy zwrócić uwagę na przedmioty lub powierzchnie, które wykazują określoną powtarzalną kolejność swoich elementów. Niektóre mozaiki, bas -relief, rzemiosło.

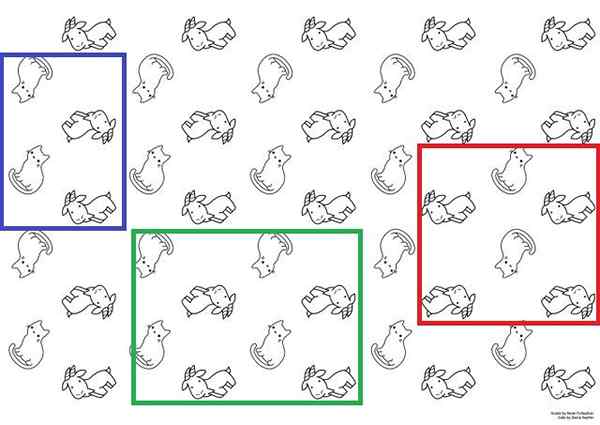Jednolite komórki na papierze kota i kozie. Źródło: Hanna Petruschat (WMDE) [CC BY-SA 4.0 (https: // creativeCommons.Org/licencje/nabrzeże/4.0)].

Aby to zilustrować, masz lepszy obraz, który mógłby być używany jako papier gobelinowy. W nim koty i kozy pojawiają się z dwoma alternatywnymi zmysłami; Koty to stopy lub głowa, a kozy patrząc w górę lub w dół.

Te koty i kozy ustalają powtarzalną sekwencję strukturalną. Aby zbudować cały papier, wystarczy odtworzyć jednolitą komórkę według powierzchni wystarczająca liczba razy, poprzez ruchy translacyjne.

Możliwe komórki jednostkowe są reprezentowane z niebieskimi, zielonymi i czerwonymi skrzynkami. Każdy z tych trzech można wykorzystać do uzyskania papieru; Ale konieczne jest ich wyobraźnie wzdłuż powierzchni, aby dowiedzieć się, czy odtwarzają tę samą sekwencję obserwowaną na obrazie.

Począwszy od czerwonego pudełka, byłoby doceniane, że gdyby trzy kolumny (kotów i kóz) zostaną przeniesione w lewo, dwie kozy nie pojawiłyby się już w dolnej części, ale tylko jedno. Dlatego doprowadziłoby to do innej sekwencji i nie można go uznać za komórkę jednostkową.

Podczas gdy wyobraźnie przemieszczają dwa pudełka, niebieskie i zielone, uzyskano tę samą sekwencję papierową. Oba są komórkami jednostkowymi; Jednak niebieskie pudełko jest bardziej przestrzegane definicją, ponieważ jest mniejsze niż zielone pudełko.

[TOC]

Właściwości komórek jednostkowych

Jego własna definicja, oprócz nowo wyjaśnionego przykładu, wyjaśnia kilka jej właściwości:

-Jeśli poruszają się w przestrzeni, niezależnie od kierunku, zostanie uzyskana pełna stała lub szkło. Wynika to z faktu, że, jak wspomniano z kotami i kozami, odtwarzają sekwencję strukturalną; który jest równy rozkładowi przestrzenne powtarzających się jednostek.

-Muszą być tak małe, jak to możliwe (lub zajmować niewielką objętość) w porównaniu z innymi możliwymi opcjami komórkowymi.

Może ci służyć: kwas metylomalonowy: struktura, właściwości, synteza, zastosowania

-Są zwykłe, symetryczne. Podobnie jego symetria jest dosłownie odzwierciedlona w kryształach związku; Jeśli komórka jednostkowa soli jest sześcienna, jej kryształy będą sześcienne. Istnieją jednak struktury krystaliczne opisane z komórkami jednostkowymi z zniekształconymi geometrią.

-Zawierają powtarzające się jednostki, które można zastąpić punktami, które z kolei trzy -wymiarowo. W poprzednim przykładzie koty i kozy reprezentują punkty siatkowe, widoczne z wyższej płaszczyzny; to znaczy dwa wymiary.

Liczba powtarzających się jednostek

Powtarzalne jednostki lub punkty siatkowe komórek jednostkowych utrzymują ten sam odsetek cząstek stałych.

Jeśli liczba kotów i kóz zostanie zliczona w niebieskim pudełku, będą dwa koty i kozy. To samo dotyczy zielonego pudełka, a także z czerwonym pudełkiem (nawet jeśli wiadomo już, że nie jest to komórka jednostkowa).

Załóżmy na przykład, że koty i kozy są odpowiednio atomami G i C (dziwne spawanie zwierząt). Ponieważ proporcja między G i C wynosi 2: 2 lub 1: 1 w niebieskim polu, można się spodziewać bez błędów, że ciało stałe będzie miało formułę GC (lub CG).

Gdy stała ma mniej lub bardziej zwarte struktury, jak w przypadku soli, metali, tlenków, sulfidów i stopów, w komórkach jednostkowych nie ma całej powtarzalnych jednostek; to znaczy są ich części lub ich części, które sumują się do jednej lub dwóch jednostek.

Nie dotyczy to GC. Jeśli niebieskie pudełko „uruchomi się” dla kotów i kóz w dwóch (1/2G i 1/2c) lub czterech części (1/4g i 1/4c). W następnych sekcjach widać, że w tych komórkach jednostkowych punkty siatkowe są wygodnie podzielone na ten i inne sposoby.

Jakie stałe sieci definiują komórkę elementarną?

Jednolitowe komórki przykładu GC są dwukierunkowe; Jednak nie ma to zastosowania w rzeczywistych modelach, które uwzględniają trzy wymiary. Zatem pudełka lub równoległoboki są przekształcane w równoległe. Teraz termin „komórka” nabiera większego sensu.

Wymiary tych komórek lub równoległości zależą od tego, jak długo są ich odpowiednie strony i kąty.

Na dolnym obrazie masz dolny tylny róg równoległości, złożony z boków Do, B I C, oraz kąty α, β i γ.

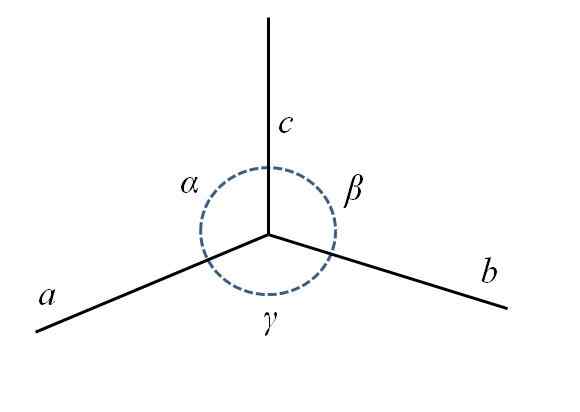Parametry komórki jednostkowej. Źródło: Gabriel Bolívar.

Jak widzisz, Do jest trochę dłużej niż B I C. W środku masz okrąg z kropkowaną linią wskazującą kąty α, β i γ, pomiędzy AC, CB I BA, odpowiednio. Dla każdej komórki elementarnej parametry mają stałe wartości i definiują ich symetrię i resztę szkła.

Może ci służyć: nadtlenek wapnia (CAO2): właściwości, ryzyko i zastosowania

Zastosując ponownie wyobraźnię, parametry obrazu zdefiniowałyby komórkę podobną do rozciągniętego sześcianu na krawędzi Do. Zatem komórki jednostkowe powstają z różnymi długościami i kątami krawędzi, które można również podzielić na różne typy.

Chłopaki

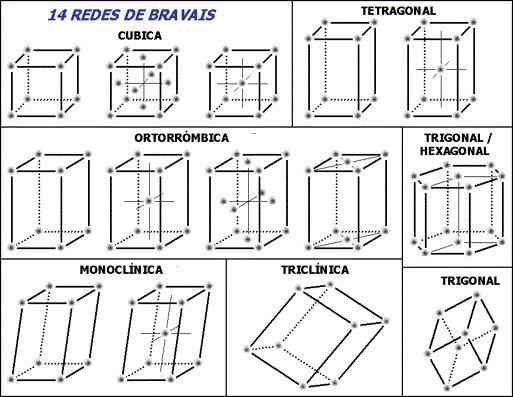
14 sieci Bravais i siedem podstawowych systemów krystalicznych. Źródło: Oryginalny przesyłanie był gniewnie w portugalskiej Wikipedii. [CC BY-SA 3.0 (http: // creativeCommons.Org/licencje/by-sa/3.0/]]

Uwaga, aby uruchomić kropkowane linie w komórkach jednostkowych: Wskazują one dolnego kąta z tyłu, jak wyjaśniono. Można zadać następujące pytanie, gdzie są punkty siatkowe lub powtarzające się jednostki? Chociaż powodują złe wrażenie, że komórki są puste, w ich wierzchołkach leży odpowiedź.

Komórki te są generowane lub wybierane w taki sposób, że w ich wierzchołkach znajdują się powtarzające się jednostki (szare punkty obrazu). W zależności od wartości parametrów ustalonych w poprzednim rozdziale, stała dla każdej komórki jednostkowej, uzyskuje siedem układów krystalicznych.

Każdy układ krystaliczny ma własną jednolitą komórkę; Drugi definiuje pierwszy. Na górnym obrazie znajduje się siedem pudeł, odpowiadających siedmiu układom krystalicznym; lub trochę więcej podsumowania, sieci krystaliczne. Zatem na przykład komórka jednostkowa sześcienna odpowiada jednym z układów krystalicznych, który definiuje sześcienną sieć krystaliczną.

Zgodnie z obrazem systemy lub sieci krystaliczne to:

-Sześcienny

-Tetragonalny

-Ortorbica

-Sześciokątny

-Jednoskośny

-Triclinic

-Trójkątny

Oraz w tych krystalicznych układach, które stanowią czternaście sieci Bravais; że spośród wszystkich sieci krystalicznych są one najbardziej podstawowe.

Sześcienny

W kostce wszystkie jego boki i kąty są takie same. Dlatego w tej komórce elementarnej są wypełnione:

Do = B = C

α = β = γ = 90º

Istnieją trzy sześcienne komórki jednostkowe: proste lub prymitywne, wyśrodkowane na ciele (BCC) i wyśrodkowane na twarzach (FCC). Różnice leżą w tym, jak punkty (atomy, jony lub cząsteczki) oraz w ich liczbie.

Która z tych komórek jest najbardziej zwarta? Ten, którego objętość jest bardziej zajęta punktami: sześcienny skupił się na twarzach. Zauważ, że jeśli zastąpimy punkty kotami i kozami początku, nie będą one ograniczeni do jednej komórki; Należałyby i byłyby udostępniane przez kilka. Znowu byłyby to części g lub c.

Może ci służyć: hydrocoloid

Liczba jednostek

Gdyby koty lub kozy znajdowały się w wierzchołkach, byłyby dzielone przez 8 komórek jednostkowych; To znaczy, każda komórka miałaby 1/8 g lub c. Razem lub wyobraź sobie 8 kostek, w dwóch kolumnach dwóch rzędów, aby to zobrazować.

Gdyby koty lub kozy były na twarzach, byłyby one dzielone tylko przez 2 komórki jednostkowe. Aby to zobaczyć, wystarczy zebrać dwie kostki.

Z drugiej strony, gdyby kot lub koza znajdowały się w centrum kostki, należałyby tylko do jednej jednolitej komórki; To samo dzieje się z pola głównego obrazu, kiedy koncepcja została rozwiązana.

Powiedział wtedy powyższe, w prostej komórce sześciennej A Jednostka lub punkt siatkowy, ponieważ ma 8 wierzchołków (1/8 x 8 = 1). W przypadku komórki sześciennej wyśrodkowanej w ciele masz: 8 wierzchołków, które są równe atomowi, i punkt lub jednostkę w środku; Dlatego jest dwa jednostki.

A dla komórki sześciennej wyśrodkowanej na twarzach: 8 wierzchołków (1) i sześć twarzy, w których dzielona jest połowa każdego punktu lub jednostki (1/2 x 6 = 3); Dlatego ma cztery jednostki.

Tetragonalny

Podobne komentarze można wykonać w odniesieniu do jednolitej komórki dla układu tetragonalnego. Jego parametry strukturalne są następujące:

Do = B ≠ C

α = β = γ = 90º

Ortorbica

Parametry dla komórki ortorombowej to:

Do ≠ B ≠ C

α = β = γ = 90º

Jednoskośny

Parametry dla komórki monoklinicznej to:

Do ≠ B ≠ C

α = γ = 90º; β ≠ 90º

Triclinic

Parametry dla komórki trójklinowej to:

Do ≠ B ≠ C

α ≠ β ≠ γ ≠ 90º

Sześciokątny

Parametry komórki sześciokątnej to:

Do = B ≠ C

α = β = 90º; γ ≠ 120º

W rzeczywistości komórka stanowi trzecią część heksagonalnego pryzmatu.

Trójkątny

I wreszcie parametry dla komórki trygonalnej to:

Do = B = C

α = β = γ ≠ 90º

Bibliografia

1. Whitten, Davis, Peck i Stanley. (2008). Chemia. (8 wyd.). Cengage Learning P 474-477.
2. Shiver & Atkins. (2008). Chemia nieorganiczna. (Czwarta edycja). MC Graw Hill.
3. Wikipedia. (2019). Komórka prymitywna. Źródło: w:.Wikipedia.org
4. Bryan Stephanie. (2019). Komórka jednostkowa: parametry latice i struktury sześcienne. Badanie. Odzyskane z: Study.com
5. Centrum zasobów akademickich. (S.F.). Struktury krystaliczne. [PDF]. Illinois Institute of Technology. Źródło: Web.iit.Edu
6. Belford Robert. (7 lutego 2019). Kryształowe leczenia i komórki jednostkowe. Chemia librettexts. Odzyskane z: chem.Librettexts.org