Jednostki pojemności, wzory, obliczenia, przykłady

Pojemność Jest to związek między obciążeniem kondensatora lub trenera, mierzonego w kulombowcu a jego potencjałem elektrycznym lub napięciem, mierzonym w woltach. Jest wyrażany w jednostkach Faradio (F), na cześć Michaela Faradaya (1791–1867).

Pojemność jest również definiowana jako właściwość lub pojemność kondensatora lub zestawu kondensatorów elektrycznych, które są mierzone przez ilość ładunku elektrycznego, które można przechowywać osobno na jednostkę zmiany potencjału elektrycznego.

Lampy, a także każde inne urządzenie elektryczne, muszą częścią ich działania do pojemności. Źródło: Pixabay.

Termin pojemność jest wprowadzana w wyniku utworzenia urządzenia elektrycznego zwanego pojemnikiem, wynalezionym przez pruskiego naukowca Ewalda Georg von Kleist, w 1745 r. I niezależnie od holenderskiego fizyka Pietera van Musschenbroekka.

Kondensatory to urządzenia elektryczne, które przechowują ładunek elektryczny i pobierają go natychmiast. Ta właściwość była używana w wielu urządzeniach elektrycznych, takich jak telewizja, radio, lampy, komputer, między innymi w życiu codziennym.

[TOC]

Kondensator i pojemność

Kondensator lub kondensator składa się z dwóch kierowców, którzy mają równe obciążenia i w inny sposób. Kierowcy nazywane są zbroją lub płytami kondensacyjnymi.

Płytka jest połączona z dodatnim (+) zaciskiem jednego baterii, podczas gdy druga płyta jest połączona z ujemnym (-). Ponieważ płytki mają równe obciążenia i przeciwny znak, obciążenie netto kondensatora wynosi zero (0).

Pojemność to związek między obciążeniem sterownika lub przewodników, które tworzą kondensator i wartość różnicy napięcia między płytkami skraplaczowymi.

Może ci służyć: Rosario czynnik chłodniczy

Jednostki i formuły

Formuła pojemności jest następująca:

C = q / v

Gdzie C jest pojemność, Q obciążenie (którego jednostką jest kulomb) i v  Napięcie (wolt)

Jednostką pojemności jest Faradio (F), co jest równoważne Coulomb / Voltio. Faradio jest bardzo dużą jednostką, więc stosuje się mikrofradium (µF), co odpowiada 10^-6 Farad; lub szczyt Faradio (PF), który jest równoważny 10^-12 Farad.

Jak obliczana jest pojemność?

Jaka będzie wartość pojemności kondensatora, którego płyty mają obciążenie 5,10^-3 Coulomb i różnica napięcia 6 woltów?

Zastosowanie formuły, którą rozwiązujemy:

C = q / v

= (5 · 10^-3 Coulomb) / (6 woltów)

= 8,33 · 10^-4  Farad

Przykłady

Wzór pojemności różni się w zależności od rodzaju kondensatora.

Kondensator równoległy

C = kε_alboA / D

K jest stałą dielektryczną, która ma wartość 1 w powietrzu i pustce. Z tego powodu formuła jest zredukowana do:

C = ε_alboA / D

ε_albo Jest to stała dielektryczna, której wartość jest blisko 8 854 · 10^-12 F · m^-1, A to obszar lub powierzchnia równoległych płyt wyrażonych w m², chwila D Odległość oddzielająca płytki równoległe.

Kondensator sferyczny

C = 4πε_alboR

Gdzie r jest promieniem kuli w metrach.

Koncentryczne kule

C = 4πε_albo / (1/ r₁ - 1/r₂)

Koncentryczny kondensator cylindra

C = 2πε_albol/ln (r₂ / R₁)

Gdzie L to długość koncentrycznych cylindrów w metrach.

Rozwiązane ćwiczenia

Kondensator równoległych płaskich płyt

Jaka będzie pojemność kondensatora lub kondensatora w powietrzu z obszarem jego 3 cm płyt² i oddzielone odległością 2 mm?

Może ci służyć: 12 przykładów baz chemicznych

Mamy formułę:

C = ε_alboOgłoszenie

I dane:

ε_albo = 8 854 x 10^-12 F · m^-1

A = 3 cm² (3 · 10^-4 M²)

D = 2 mm (2,10^-3 M)

Przejdź do wymiany:

C = (8 854 · 10^-12 F · m^-1) (3 · 10^-4 M²) / (2 · 10^-3 M)

= 1 3281 · 10^-14 F

Kondensator lub kufak w kształcie

Jeśli ziemia jest uważana za kulisty kondensator o promieniu (r) 6.370 km: jaka będzie wartość twojej pojemności?

Dane:

C = 4πε_alboR

Π = 31416

ε_albo = 8 854 · 10^-12 F.M^-1

R = 6.370 km (6,37 · 10⁶ M)

Wartości w formule pojemności są ponownie zastąpione:

C = (4 · 31416) (8 854 · 10^-12 F · m^-1) (6,37 · 10⁶ M)

= 7,09 · 10^-8 F

= 709 µF

Połączenie kondensatorów

Kondensatory lub kondensatory można łączyć w szeregu lub równolegle.

Kondensatory serii

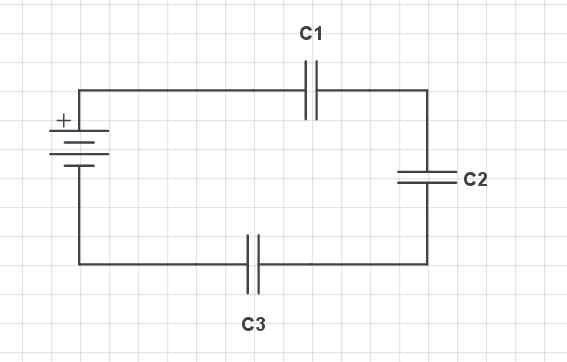Kondensatory serii. Źródło Gabriel Bolívar przez obwód

Górny obraz pokazuje trzy kondensatory serii (c₁, C₂ i C₃), a także bateria z dodatnimi (+) i ujemnymi (--) terminami. Te kondensatory mają szereg cech w odniesieniu do ich napięcia, obciążenia i pojemności.

Spadek napięcia (δv) w kondensatorach

Δv_T = Δv₁   +   Δv₂   +    Δv₃

Całkowity spadek napięcia w zestawie kondensatorów szeregowych jest równy sumie upadków napięcia kondensatorów.

Ciężar  kondensatorów

Q_T = Q₁ = Q₂ = Q₃

Ta sama ilość obciążenia krąży w serii.

Pojemność pojemności

Równoważna pojemność kondensatorów szeregowych przedstawia następującą relację:

1 c_Eq  = 1/c₁  +   1 c₂   +   1 c₃

Równoległe kondensatory

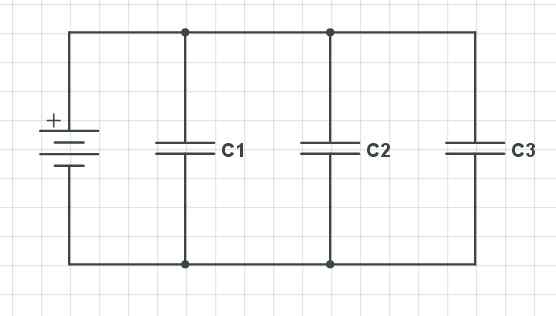Równoległe kondensatory. Źródło Gabriel Bolívar przez obwód.

W górę mamy trzy kondensatory ułożone równolegle (c₁, C₂ i C₃), które utrzymują w stosunku do spadku napięcia, obciążenia i pojemności następujące zachowanie:

Może ci służyć: alkeny

Spadek napięcia w kondensatorach

Δv_T  = Δv₁  = Δv₂  = Δv₃

W równoległych kondensatorach całkowity spadek napięcia w kondensatorach jest taki sam jak istniejący dla każdego z kondensatorów.

Kondensatory

Q_T  = Q₁  +  Q₂  +  Q₃

W równoległym systemie całkowite obciążenie kondensatorów jest równe sumie obciążenia wszystkich kondensatorów.

Pojemność pojemności

C_Eq  = C₁  +  C₂   +  C₃

W równoległym układzie równoważna pojemność ich jest równa suma pojemności wszystkich kondensatorów.

Przykład ćwiczenia

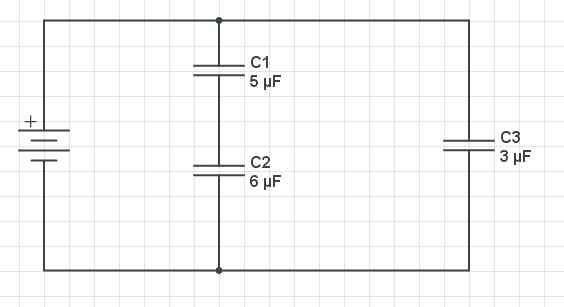Przykład problemu i równoległych kondensatorów. Źródło Gabriel Bolívar przez obwód.

Schemat trzech kondensatorów pokazano powyżej: C₁ i C₂ Są one rozmieszczone szeregowo i są równoległe z C₃. Pojemność kondensatorów jest następująca: C₁ = 5 µF, C₂ = 6 µF i C₃ = 3 µF. Znajdź równoważną pojemność obwodu.

Pierwszy to równoważna pojemność C₁ i C₂ którzy są w serii.

1 c_Eq1,2 = 1/c₁  +  1 c₂

1 c_Eq1,2 = 1/5 µF +1/6 µF

1 c_Eq1,2 = (11/30) µF

C_Eq1,2 = 30 µF / 11

= 2,72 µF

Kondensatory 1 i 2 są równoległe do C₃. Tak więc równoważna pojemność C₁, C₂ i C₃ jest równe C_Eq1,2 +  C₃.

C_Eq1,2,3 = 2,72 µF +3 µF

= 5,72 µF

Bibliografia

1. Serway, r. DO. i Jewett, J. W. (2009). Fizyka nauk i inżynierii. Głośność 2. Siódma edycja. Editorial Cengage Learning.
2. Reddick, R i Halliday, D. (1965). Fizyczny.  Część 2. Drugie wydanie po hiszpańsku. Continental Editorial s.DO.
3. Badanie. (22 kwietnia 2015 r.). Pojemność: jednostki i formuła. Odzyskane z: Study.com
4. Pusty fizyka. (S.F.). Kondensatory w szeregu i równolegle. Odzyskane z: kursów.Lumenarning.com
5. Redaktorzy Enyclopaedia Britannica. (2020). Pojemność. Odzyskane z: Britannica.com