Krawędzie kostki

Jaka jest krawędź kostki?

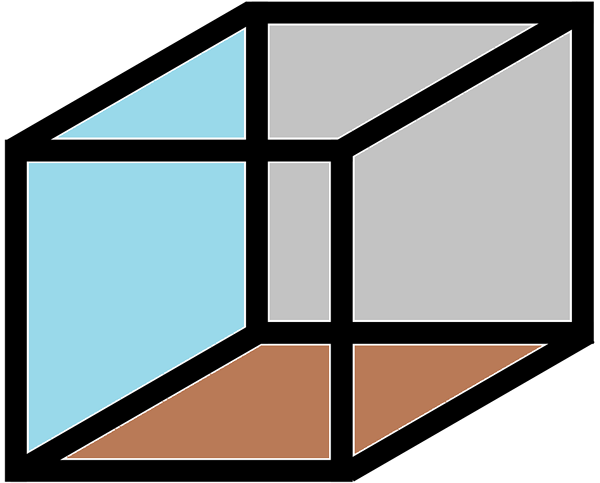
krawędź kostki Jest to krawędź: jest to linia, która łączy dwa wierzchołki lub narożniki. Krawędź to linia, w której przechwycone są dwie strony figury geometrycznej. Kostka ma 12 krawędzi.

Poprzednia definicja jest ogólna i dotyczy dowolnej liczby geometrycznej, nie tylko do kostki. Jeśli chodzi o płaską figurę, krawędzie odpowiadają bokom wspomnianej figury.

Nazywa się go równoległym do figury geometrycznej z sześcioma twarzami w postaci równoległoboków, z których przeciwieństwa są równe i równoległe do siebie.

W konkretnym przypadku, w którym twarze są kwadratowe, równoległe odniesie.

Sposoby zidentyfikowania krawędzi kostki

Aby uzyskać lepszą ilustrację, można użyć obiektów codziennych do dokładnego ustalenia, które są krawędziami kostki.

1- Armando Paper Cube

Jeśli zobaczysz, jak zbudowano papierowy lub kartonowy wiadro, możesz zobaczyć, jakie są Twoje krawędzie. Zaczyna rysować krzyż jak figura, a niektóre linie w środku są oznaczone.

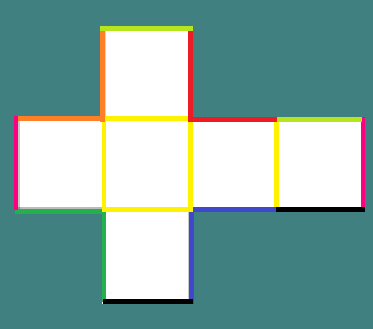
Każda z żółtych linii reprezentuje fałd, który będzie krawędzią kostki (krawędź).

Podobnie każda para linii, która ma ten sam kolor, utworzy krawędź po przyłączeniu. W sumie kostka ma 12 krawędzi.

2- Rysowanie kostki

Innym sposobem zobaczenia, jakie są krawędzie kostki, jest obserwowanie, jak jest on narysowany. Zaczynasz od rysowania kwadratu z boku L; Każda strona kwadratu jest krawędzią kostki.

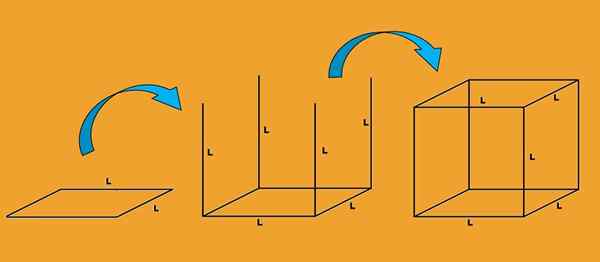
Następnie wyciągane są cztery pionowe linie z każdego wierzchołka, a długość każdej z tych linii wynosi l. Każda linia jest również krawędzią łyżki.

Wreszcie rysowany jest kolejny kwadrat L, tak że jego wierzchołki pokrywają się z końcem krawędzi narysowanych w poprzednim kroku. Każda z boków tego nowego kwadratu jest krawędzią kostki.

3- Kostka Rubik

Aby zilustrować definicję geometryczną, która wystąpiła na początku, możesz zobaczyć kostkę Rubik.

Każda twarz ma inny kolor. Krawędzie są reprezentowane przez linię, w której twarze są przechwytywane różnymi kolorami.

Twierdzenie Euler

Twierdzenie Eulera dla Polyhedros mówi, że biorąc pod uwagę wielościan, liczba twarzy C plus liczba wierzchołków V jest równa liczbie krawędzi do plus 2. To znaczy, c+v = a+2.

Na poprzednich zdjęciach widać, że kostka ma 6 twarzy, 8 wierzchołków i 12 krawędzi. Dlatego spełnia twierdzenie Eulera dla wielościanów, ponieważ 6+8 = 12+2.

Znajomość długości krawędzi kostki jest bardzo przydatna. Jeśli znana jest długość krawędzi, wówczas znana jest długość wszystkich jej krawędzi, które mogą uzyskać określone dane kostki, takie jak jego głośność.

Objętość kostki jest zdefiniowana jako l³, gdzie l jest długością jego krawędzi. Dlatego, aby poznać objętość kostki, konieczne jest tylko znanie wartości L.