Pojęcia analizy siatki, metody, przykłady

On Analiza siatki Jest to technika stosowana do rozwiązywania płaskich obwodów elektrycznych. Ta procedura może również pojawić się w literaturze z nazwami metod prądy obwodu o Metoda Prądy siatkowe (lub pętla).

Podstawą tego i innych metod analizy obwodów elektrycznych są prawo Kirchhoffa i Ohma. Z kolei prawa Kirchhoffa są wyrażeniami dwóch bardzo ważnych zasad ochrony w fizyce dla izolowanych systemów: Zarówno ładunek elektryczny, jak i energia są zachowane.

Rysunek 1. Obwody są częścią niezliczonych urządzeń. Źródło: Pixabay.

Z jednej strony ładunek elektryczny jest powiązany z prądem, który jest ruchomy obciążenie, podczas gdy w obwodzie energia jest połączona z napięciem, który jest agentem odpowiedzialnym za wykonanie niezbędnej pracy, aby utrzymać obciążenie w ruchu.

Przepisy te, zastosowane do płaskiego obwodu, generują zestaw równań jednoczesnych, które należy rozwiązać, aby uzyskać wartości prądu lub napięcia.

Układ równań można rozwiązać za pomocą znanych technik analitycznych, takich jak Reguła Cramer, który wymaga obliczenia determinantów w celu uzyskania rozwiązania systemowego.

W zależności od liczby równań są one rozwiązywane za pomocą kalkulatora naukowego lub oprogramowania matematycznego. W sieci dostępnych jest również wiele opcji.

[TOC]

Ważne warunki

Przed wyjaśnieniem, jak to działa, zaczniemy od zdefiniowania tych warunków:

Oddział: Sekcja zawierająca element obwodu.

Węzeł: punkt, który łączy dwie lub więcej gałęzi.

Wstążka: Jest to każda zamknięta część obwodu, która zaczyna się i kończy w tym samym węźle.

Siatka: pętla, która nie zawiera żadnej innej więzi w środku (Niezbędna siatka).

Metody

Analiza zbiórka jest ogólną metodą, która służy do rozwiązywania obwodów, których elementy są połączone szeregowo, równolegle lub mieszane, to znaczy, gdy rodzaj połączenia nie jest wyraźnie wyróżniony. Obwód musi być płaski, a przynajmniej musi być możliwe spłacenie go jako takiego.

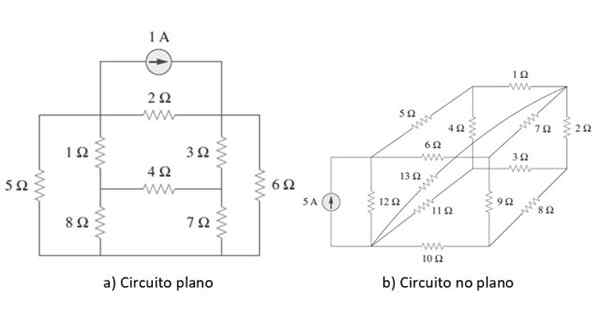Rysunek 2. Obwody płaskie i nieflatowe. Źródło: Alexander, C. 2006. Podstawy obwodów elektrycznych. 3. Wydanie. MC Graw Hill.

Przykład każdego rodzaju obwodu pokazano na powyższym rysunku. Po wyjaśnieniu punktu, na początek, zastosujemy metodę do prostego obwodu jako przykład w następnej sekcji, ale zanim krótko sprawdzimy prawa Ohm i Kirchhoff.

Prawo Ohma: Sean V Napięcie, R opór e Siema Prąd omowego elementu rezystancyjnego, w którym napięcie i prąd są bezpośrednio proporcjonalne, a rezystancja jest stałą proporcjonalności:

Może ci służyć: API Gravity: Skala i klasyfikacja ropy

V = i.R

Napięcie Kirchhoff Law (LKV): W każdej zamkniętej trajektorii przejechanej w jednym kierunku suma algebraiczna napięć wynosi zero. Obejmuje to napięcia z powodu źródeł, rezystorów, cewek lub kondensatorów: ∑ e = ∑ r_Siema. Siema

Kirchhoff z prądu (LKC): W dowolnym węźle suma algebraiczna prądów wynosi zero, biorąc pod uwagę, że prądy, które wpisuje się. W ten sposób: ∑ i = 0.

Z metodą prądów siatkowych nie jest to konieczne.

- Kroki w celu zastosowania analizy siatki

Zaczniemy wyjaśniać metodę dla obwodu o sice. Procedurę można przedłużyć później dla większych obwodów.

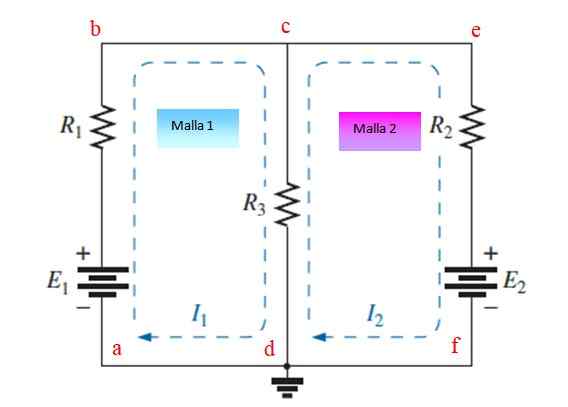Rysunek 3. Obwód z rezystancjami i źródłami ułożonymi w dwie siatki. Źródło: f. Zapata.

Krok 1

Przypisz i narysuj niezależne prądy do każdej siatki, w tym przykładzie są one Siema₁ I Siema₂. Można je narysować w harmonogramie lub także antyhoraryczne.

Krok 2

Zastosuj prawo napięć Kirchhoffa (LTK) i Ohma do każdej siatki. Potencjalne upadki przypisane są znak (-), podczas gdy podwyżki są przypisane znakowi (+).

Abcda Mesh

Zaczynając od punktu A i po znaczeniu prądu, znajdujemy wzrost potencjału w baterii E1 (+), a następnie spadek R₁ (-), a następnie kolejny spadek w r₃ (-).

Jednocześnie opór r₃ Jest również przekraczany przez prąd i₂, Ale w przeciwnym kierunku reprezentuje wzrost (+). Pierwsze równanie jest takie:

I₁-R₁.Siema₁ -R₃.Siema₁ + R₃.Siema₂ = 0

Natychmiastowa faktorowanie się i ponowne prromotowanie Warunki:

- (R₁+R₃)SIEMA₁ +R₃Siema₂ = -E₁  (Równanie 1)

CEFDC MESH 

Zaczynając od punktu I a po znaczeniu prądu jest potencjalny spadek R₂ (-), kolejny spadek I₂, ponieważ prąd wchodzi przez słupek baterii + i na koniec kolejnego spadku R₃ (-), jednocześnie prąd Siema₁ Krzyżuje się R₃ W przeciwnym kierunku (+).

Drugie równanie, ze wskazanymi znakami, pozostaje w ten sposób:

- R₂ Siema₂ - I₂ -R₃ Siema₂ +R₃ Siema₁= 0

R₃Siema₁ - (R₂ +R₃₎ Siema₂ = E₂  (Równanie 2)

Zauważ, że istnieją dwa równania z dwoma niewiadomymi i₁ i ja₂.

Krok 3

Wówczas ustanowiony układ równań jest rozwiązany.

Rozwiązane ćwiczenia

Na początek ważne jest, aby wziąć pod uwagę następujące:

-Prądy lub prądy siatki można przypisać dowolnym kierunku.

-Do każdej niezbędnej siatki - lub „okna” - aby obwodowi należy przypisać prąd.

Może ci służyć: proces izokoryczny

-Prądy siatki są wywoływane z literami kapitałowymi w celu odróżnienia ich od prądów krążących w gałęziach, chociaż w niektórych przypadkach prąd krążący przez gałąź może tak samo jak w przypadku siatki.

- Przykład 1

Znajdź prądy krążące przez każdą rezystancję w obwodzie na rycinie 3, jeśli elementy mają następujące wartości:

R₁ = 20 Ω; R₂ = 30 Ω; R₃ = 10 Ω; I₁ = 12 V; I₂ = 18 v

Rozwiązanie

Po pierwsze, należy przypisać prądy siatki i₁ i ja₂ i weź system równań, jak wydedukowano w poprzedniej sekcji, a następnie zastąp wartości podane w instrukcji:

- (R₁+R₃)SIEMA₁ +R₃Siema₂ = -E₁  (Równanie 1)

R₃Siema₁ - (R₂ +R₃₎ Siema₂ = E₂     (Równanie 2)

-

-(20+30) Siema₁ + 10i₂ = -12

10i₁ - (30 +10) i₂ = 18      

--

-pięćdziesiątSiema₁ + 10i₂ = -12

10i₁ - 40 i₂ = 18      

Ponieważ jest to układ równań 2 x 2, można go łatwo rozwiązać przez redukcję, mnożąc przez 5 równanie, aby wyeliminować nieznane Siema₁:

-pięćdziesiątSiema₁ + 10 i₂ = -12

50i₁ - 200 i₂ = 90

-     

-190 i₂= 78

Siema₂ = - 78/180 A = - 0.41 a

Prąd jest natychmiast usuwany Siema₁ dowolnego z oryginalnych równań:

Siema₁ = (18 + 40 i₂) / 10 = (18 + 40 x (-0.41)) / 10 = 0.16 a

Znak ujemny w prądu Siema₂ oznacza, że ​​prąd w 2 siatce krąży wbrew rysunku.

Prądy w każdym oporze są następujące:

Dla oporu R₁ Prąd krąży Siema₁ = 0.16 a w tym sensie narysowanym przez opór R₂ Prąd krąży Siema₂ = 0.41 a w przeciwieństwie do narysowania i oporu R₃ krąży Siema₃ = 0.16- (-0.41) A = 0.57 a w dół.

Rozwiązanie systemowe metodą Cramera

W sposób matrycy system można rozwiązać w następujący sposób:

Krok 1: Oblicz δ

 Ważny: Gdy δ = 0, system nie ma rozwiązania, jest to niekompatybilny system.

Krok 2: Oblicz δ₁

Pierwsza kolumna jest zastępowana niezależnymi warunkami systemu równań, utrzymując kolejność, w jakiej system został pierwotnie podniesiony:

Krok 3: Oblicz i₁

Siema₁ = Δ₁/Δ = 300/1900 = 0.16 a

Krok 4: Oblicz δ₂

 Krok 5: Oblicz i₂

Siema₂ = Δ₂/Δ = -780/1900 = -0.41 a

- Przykład 2

Określ prąd i napięcia przez każdą rezystancję w następującym obwodzie, metodą prądów z siatki:

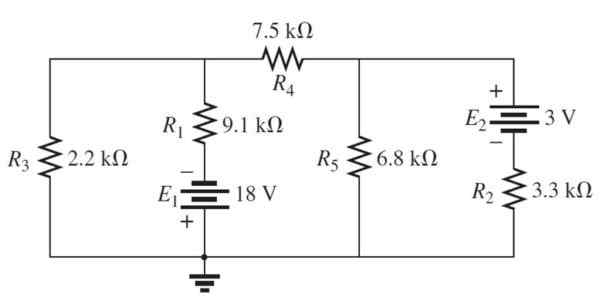Rysunek 4. Obwód o siatkę. Źródło: Boylestad, r. 2011. Wprowadzenie do analizy obwodów.2. Wydanie. osoba.

Rozwiązanie

Trzy prądy siatki są rysowane, jak pokazano na poniższym rysunku, w arbitralnych zmysłach. Teraz siatki działają z dowolnego miejsca:

Może ci służyć: Imantacja: co polega na metodzie i przykładach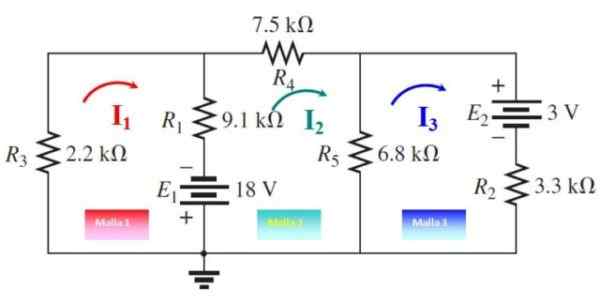 Rysunek 5. Prądy siatkowe do ćwiczenia 2. Źródło: f. Zapata, zmodyfikowane z Boylestad.

Siatka 1

-9100.Siema₁+18-2200.Siema₁+9100.Siema₂= 0

-11300 i₁ + 9100.Siema₂ = -18

Siatka 2       

-(7500 +6800 +9100) .Siema₂ + 9100.Siema₁+6800.Siema₃-18 = 0

9100.Siema₁ - 23400.Siema₂ + 6800.Siema₃ = 18

Siatka 3  

-(6800 + 3300) i₃ + 6800.Siema₂ - 3 = 0

6800.Siema₂ - 10100.Siema₃ = 3

Układ równań

-11300 i₁ + 9100.Siema₂ + 0.Siema₃= -18

9100.Siema₁ - 23400.Siema₂ + 6800.Siema₃ = 18

0.Siema₁ + 6800.Siema₂ - 10100.Siema₃ = 3

Chociaż liczby są duże, szybko się rozwiązywano za pomocą kalkulatora naukowego. Pamiętaj, że równania muszą być zamówione i dodać zer w miejscach, w których nieznany nie pojawia się, jak się tutaj pojawia.

Prądy siatki to:

Siema₁ = 0.0012 A; Siema₂ = -0.00048 a; Siema₃ = -0.00062 a

Prądy Siema₂ I Siema₃ Krążą w przeciwnym kierunku na rysunku, ponieważ okazały się negatywne.

Tabela prądów i napięć w każdej oporności

Rezystancja (ω)	Bieżące (wzmacniacze)	Napięcie = i.R (wolty)
9100	Siema1 -Siema2 = 0.0012-(-0.00048) = 0.00168	piętnaście.3
3300	0.00062	2.05
2200	0.0012	2.64
7500	0.00048	3.60
6800	Siema2 -Siema3= -0.00048-(-0.00062) = 0.00014	0.95

Rozwiązanie reguły Cramer

Ponieważ są to duże liczby, wygodne jest wykorzystanie notacji naukowej do bezpośredniej pracy z nimi.

Obliczanie i₁

Strzałki kolorowe w wyznaczniku 3 x 3 wskazują, jak znaleźć wartości numeryczne, pomnożając wskazane wartości. Zacznijmy od uzyskania pierwszego wspornika w wyznaczniku δ:

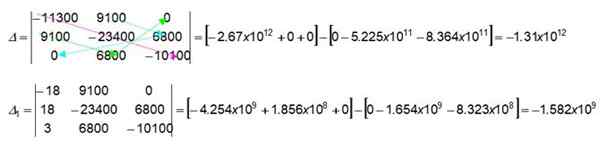
(-11300) x (-23400) x (-10100) = -2.67 x 10¹²

9100 x 0 x 0 = 0

9100 x 6800 x 0 = 0

Natychmiast otrzymujemy drugi wspornik w tym samym wyznaczniku, który działa od lewej do prawej (dla tego wspornika kolorowe strzałki nie zostały narysowane na rysunku). Zapraszamy czytelnika do jego zweryfikowania:

0 x (-23400) x 0 = 0

9100 x 9100 x (-10100) = -8.364 x 10^jedenaście

6800 x 6800 x (-11300) = -5.225 x 10^jedenaście

W ten sam sposób czytelnik może również zweryfikować wartości wyznacznika Δ₁.

Ważny: Pomiędzy obiema nawiasami zawsze występuje znak ujemny.

Wreszcie prąd jest uzyskiwany Siema₁ Poprzez Siema₁ = Δ₁ / Δ

Siema₁ = -1.582 x 10⁹/-1.31 x 10¹² = 0.0012 a                                   

Obliczanie i₂

Procedurę można powtórzyć do obliczenia Siema₂, W takim przypadku, aby obliczyć determinant δ₂ Druga kolumna wyznacznika δ jest zastąpiona kolumną niezależnych warunków, a jego wartość jest znaleziona, zgodnie z wyjaśnioną procedurą.

Jednak, jak to jest uciążliwe z powodu dużych liczb, zwłaszcza jeśli nie ma kalkulatora naukowego, najprostsze jest zastąpienie wartości Siema₁ już obliczone, w następującym równaniu i jasne:

-11300 i₁ + 9100.Siema₂ + 0.Siema₃= -18 → 9100 i₂= -18 + 11300 i₁ → i₂ = -0.00048 a

Obliczanie i3

Raz z wartościami Siema₁ I Siema₂ W ręku, Siema₃ Jest to bezpośrednio znalezione przez substytucję.

Bibliografia

1. Alexander, c. 2006. Podstawy obwodów elektrycznych. 3. Wydanie. MC Graw Hill.
2. Boylestad, r. 2011. Wprowadzenie do analizy obwodów.2. Wydanie. osoba.
3. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 5. Interakcja elektryczna. Pod redakcją Douglas Figueroa (USB).
4. Garcia, L. 2014. Elektromagnetyzm. 2. Wydanie. Uniwersytet przemysłowy Santander.
5. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Głośność 2.