Charakterystyka wektorów równoległych, przykłady i ćwiczenia

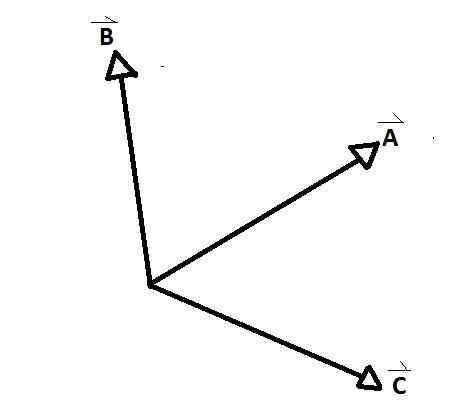
Wektory współbieżne Są to grupy wektorów, których osie pokrywają się w jednym punkcie, tworząc między nimi kąt wewnętrzny i zewnętrzny. Wyraźny przykład obserwuje się na dolnej figurze, gdzie A, B i C są ze sobą współbieżnymi wektorami.

D i E w przeciwieństwie do reszty nie są. Istnieją kąty wśród współbieżnych wektorów AB, AC i CB. Nazywane są kąty relacji między wektorami.

[TOC]

Charakterystyka

-Mają wspólny punkt, który pokrywa się z ich pochodzeniem: wszystkie wielkości współbieżnych wektorów zaczynają się od wspólnego punktu do ich odpowiednich skrajności.

-Pochodzenie jest uważane za punkt działania wektorowego: należy ustalić punkt działania, na który wpłynie bezpośrednio każdy z współbieżnych wektorów.

-Twoja domena w płaszczyźnie i przestrzeni jest R² i r³ odpowiednio: Wektory współbieżne mogą swobodnie pokryć całą przestrzeń geometryczną.

-Pozwala na różne notacje w tej samej grupie wektorów. Według gałęzi badań, w operacjach z wektorami występują różne zapisy.

Rodzaje wektorów

Gałąź wektorów ma wiele podziałów, wśród niektórych można je wyznaczyć: równolegle, prostopadłe, coplanarios, odpowiadające, przeciwne i jednolite. Wektory współbieżne pojawiają się na tej liście i podobnie jak wszystkie wcześniej wyznaczone, mają wiele wniosków w różnych naukach.

Są bardzo powszechne w badaniu wektorowym, ponieważ reprezentują opłacalne uogólnienie w operacjach z nimi. Zarówno w płaszczyźnie, jak i w przestrzeni, współbieżne wektory są do bieżącego zastosowania do reprezentacji różnych elementów i badają ich wpływ na dany system.

Notacja wektorowa

Istnieją różne sposoby reprezentowania elementu wektora. Główne i najbardziej znane to:

kartezjański

Zaproponowane przez to samo matematyczne podejście, oznacza wektory z listą odpowiadającą wielkościom każdej osi (x, y, z)

A: (1, 1, -1) Space A: (1, 1) planuj

Polarny

Służy one tylko do oznaczania wektorów w płaszczyźnie, chociaż w obliczeniach całkowym przypisuje się komponent głębokości. Składa się z wielkością liniową R i kąt w odniesieniu do osi polarnej Ɵ.

Może ci służyć: statystyki wnioskowania: historia, cechy, do czego służy przykłady

Odp.: (3, 45⁰ ) Plan A: (2, 45⁰ , 3) Przestrzeń

Analityczny

Zdefiniuj wielkości wektora przez versors. Versorory (R&E + K) reprezentują wektory jednostkowe odpowiadające osiom X, y I

A: 3i + 2J - 3k

Kulisty

Są podobne do notacji polarnej, ale z dodaniem drugiego kąta, który zamiatuje się na płaszczyźnie Xy symbolizowane przez δ.

Odp.: (4, 60^albo , π/4)

Operacje z współbieżnymi wektorami

Wektory współbieżne są najczęściej używane do definiowania operacji między wektorami, ponieważ łatwiej jest porównać elementy wektorów, gdy występują w sposób jednoczesny.

Suma (a + b)

Suma współbieżnych wektorów ma na celu znalezienie powstałego wektora V_R. Który, zgodnie z gałęzią badań, odpowiada ostatecznemu działaniu

Na przykład: 3 sznurki są powiązane a, b, c do pudełka, każdy koniec liny znajduje się w rękach tematu. Każdy z 3 osób musi wyciągnąć linę w innym kierunku niż pozostałe 2.

A: (AX, AY, AZ) B: (BX, BY, BZ) C: (CX, CY, CZ)

A+b+c = (ax+bx+cx; ay+przez+cy; az+bz+c) = V_R

Dlatego pudełko może poruszać się tylko w jednym kierunku V_R Wskazuje kierunek i poczucie przemieszczenia pudełka.

Różnica (a - b)

Istnieje wiele kryteriów dotyczących różnicy między wektorami, wielu autorów decyduje się go wykluczyć i twierdzi, że tylko suma między wektorami jest określona, ​​gdzie różnica jest sumą przeciwnego wektora. Prawda jest taka, że ​​wektory algebraicznie można odejmować.

A: (Ax, ay, az) B: (Bx, BY, Bz)

A-b = a + (-b) = (ax-bx; ay-be; az-bz) = [ax + (-bx); ay + (-By); AZ + (-bz)]

Produkt skalarny (a . B)

Znany również jako produkt Punto, generuje wartość skalarną, która może być powiązana z kilkoma wielkościami zgodnie z gałęzią badania.

Dla geometrii wskazuje obszar równoległoboku utworzony przez parę równoczesnych wektorów za pomocą metody równoległoboku. Dla fizyki mechanicznej określa pracę wykonaną siłą F Przesuwając ciało na odległość ΔR.

Może ci służyć: proporcjonalność złożona: wyjaśnienie, trzy złożone reguły, ćwiczenia

ѡ = f . ΔR

Jak sama nazwa wskazuje, generuje wartość skalarną i jest zdefiniowana w następujący sposób:

Być wektorami a i b

A: (Ax, ay, az) B: (Bx, BY, Bz)

-Forma analityczna:

( DO . B) = | A |.| B |.Cos θ

Gdzie θ jest wewnętrznym kątem między obiema wektorami

-Forma algebraiczna:

( DO . B) = (AX.BX + AY.przez + az.BZ)

Produkt wektorowy (a x b)

Wektor lub produkt punktowy między dwoma wektorami definiuje trzeci wektor C to ma jakość bycia prostopadłym B I C. W fizyce określa moment obrotowy wektor τ Podstawowy element dynamiki rotacyjnej.

-Forma analityczna:

|. A x b | = | A |.| B |.Sin θ

-Forma algebraiczna:

(A x B) = = (AX . przez - ay . Bx)- (AX . BZ - AZ . Bx) J + (Topór . przez - ay . Bx) k

-Ruch względny: r_A/b

Podstawą względności jest ruch względny, a równoległe wektory są podstawą ruchu względnego. Możesz wydedukować pozycje, prędkości i względne przyspieszenia, stosując następującą kolejność pomysłów.

R _A/b = r_DO - R_B    ; Względna pozycja dotycząca B

v _A/b = v_DO - v_B  ; Względna prędkość szacunku do B

Do _A/b = a_DO - Do_B  ; Względne przyspieszenie szacunku dla B

Przykłady: Rozwiązane ćwiczenia

Ćwiczenie 1

Niech wektory współbieżne A, B i C.

A = (-1, 3, 5) b = (3, 5, -2) c = (-4, -2, 1)

-Zdefiniuj wynikowy wektor V_R = 2a - 3b + c

2a = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)

-3B = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)

V_R = 2a + (-3b) + c = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)

V_R = ([-2+(-9)+(-4)]; [6+(-15)+(-2)]; (10+6+1)))

V_R = (-15, -11, 17)

-Zdefiniuj produkt skalarny (a . C)

( DO . C) = (-1, 3, 5) . (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4-6 + 5

( DO . C) = 3

-Oblicz kąt między A i C

( DO . C) = | a |.| C |.Cos θ gdzie θ jest najkrótszym kątem wśród wektorów

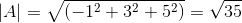
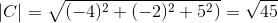
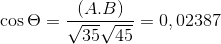
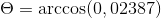
θ = 88,63⁰

 -Znajdź wektor prostopadły do ​​A i B

W tym celu konieczne jest zdefiniowanie produktu wektora między (-1, 3, 5) i (3, 5, -2). Jak wyjaśniono wcześniej, zbudowana jest matryca 3 x 3, w której pierwszy rząd składa się z listy wektorów jednostkowych (I, J, K). Następnie drugi i trzeci rząd składa się z wektorów do obsługi.

Może ci służyć: notacja dziesiętna

(A x B) = = [(-1) . 5 - (3 . 3)] Siema  - [(-1) . (-2) - (5 . 3)] J + [(-1) . 5 - (3 . 3)] k

(A x B) = (-5 - 9) Siema - (2 - 15) J + (-5 - 9) k         

(A x B) =  -14 i + 13 J - 14 K

Ćwiczenie 2 

Niech v_Do i v_B Wektory prędkości odpowiednio A i B. Oblicz prędkość B na podstawie.

V_Do = (3, -1, 5) v_B = (2, 5, -3)

W tym przypadku wymagana jest względna prędkość B V_B/a

V_B/a = V_B - V_DO

V_B/a = (2, 5, -3) -(3, -1, 5) = (-1, 6, -8)

To jest wektor Veloc B widziany z A. Gdzie nowy wektor prędkości B jest opisany przez odniesienie do obserwatora ustawionego w a i poruszającym się z prędkością.

Proponowane ćwiczenia

1-konstruktu 3 wektory A, B i C, które są jednocześnie i opowiadają 3 operacje między nimi poprzez praktyczne ćwiczenie.

2 -Wektory A: (-2, 4, -11), B: (1, -6, 9) i C: (-2, -1, 10). Znajdź wektory prostopadłe do: a i b, c i b, suma a + b + c.

4-determina 3 wektory, które są do siebie prostopadłe, bez uwzględnienia osi współrzędnych.

5 Odefiniuj pracę wykonaną siłą, która podnosi 5 kg bloku masy, z dna studni o głębokości 20 m.

6-Swamker Algebraica, że ​​odejmowanie wektorów jest równe sumie przeciwnego wektora. Uzasadnić swoje postulaty.

7-deenote wektor we wszystkich notacjach opracowany w tym artykule. (Kartezjański, polarny, analityczny i sferyczny).

8-Siły magnetyczne wywierane na magnes, który spoczywa na tabeli, są podawane przez następujące wektory; V: (5, 3, -2), T: (4, 7, 9), H: (-3, 5, -4). Określ w jakim kierunku magnes porusza się, jeśli wszystkie siły magnetyczne działają jednocześnie.

Bibliografia

1. Geometria i transformacje euklidesowe. Clayton w. Unik. Couer Corporation, 1 stycznia. 2004
2. Jak rozwiązać problemy z matematyką l. Moiseiwitsch. Couer Corporation, 10 kwietnia. 2013
3. Podstawowe pojęcia geometrii. Walter Prenowz, Meyer Jordan. Rowman & Littlefield, 4 października. 2012
4. Wektory. Rocío Navarro Lacoba, 7 czerwca. 2014
5. Algebra liniowa. Bernard Kolman, David R. WZGÓRZE. Pearson Education, 2006