Matematyka

Zmiana proporcjonalna

Zmiana proporcjonalna

Co to jest proporcjonalna zmienność?

Zmiana proporcjonalna między dwiema zmiennymi „x” i „y” zachodzi, gdy, pomnożąc jedną z nich przez jedną stałą, druga jest również pomnożona lub podzielona przez tę samą stałą. Wiele rzeczywistych sytuacji można odpowiednio z nimi opisać.

Proporcjonalność między zmiennymi może być bezpośrednia lub odwrotna. W bezpośrednim proporcjonalności związek jest typu:

y = k ∙ x

Lub równoważnie:

K = y/x

Gdzie k jest stałym nazywanym stała proporcjonalności albo Stosunek proporcjonalności. Zauważ, że jeśli „X” wzrośnie, „y” czyni to w tej samej proporcji, a jeśli „x” zmniejszy się, również „y”. Gdy zależność między zmiennymi jest wykresem, uzyskuje się linię prostą, która przechodzi przez pochodzenie układu współrzędnych (patrz ćwiczenie rozwiązane później).

Bezpośrednia zmienność może również wystąpić między jedną zmienną a jedną mocą drugiej, na przykład, „y” może być wprost proporcjonalne do x2, X3 a więc.

Z drugiej strony, w odwrotnej proporcjonalności, zmienne są powiązane przez wyrażenie:

x ∙ y = k

To wyrażenie oznacza, że ​​iloczyn zmiennych jest stały. Podczas wykresu związku między zmiennymi jest hiperbola. Ponadto, jeśli produkt zmiennej o jednej mocy drugiej jest stały, reprezentuje również przypadek odwrotnej proporcjonalności, na przykład:

X2∙ y = k; X3∙ y = k ..

Przykłady

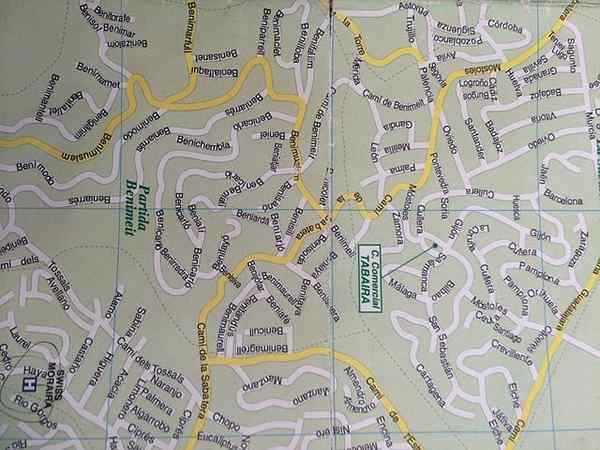Zastosowanie proporcjonalnej zmienności to układ map

Wiele praw fizyki i chemii wyraża się matematycznie jako proporcje. Na przykład siła, która wywiera sprężynę i wydłużenie tego samego, związek między ciśnieniem a objętością w gazie w stałej temperaturze, okres prostego wahadła i pierwiastek kwadratowy o jego długości i wiele innych. Znając modelu, który rządzi tym zjawiskiem, możesz znaleźć swoje zachowanie dla dowolnej wartości zmiennych.

Może ci służyć: twierdzenie o istnieniu i wyjątkowości: demonstracja, przykłady i ćwiczenia

I nie tylko to stosują się również w niezliczonych sytuacjach:

  • Przekaż wzór odzieży o mniejszym rozmiarze do większego rozmiaru (lub odwrotnie).
  • W czynnikach konwersji, aby przejść z jednej jednostki do drugiej, takich jak kilometry do mil, galony do litrów i nie tylko.
  • Oblicz składniki przepisu dla 6 osób, znając wymóg dla 4 osób.
  • Określ kwotę niektórych podatków zgodnie z uzyskanym dochodem.
  • W obliczaniu prostego zainteresowania.
  • Podczas rysowania samolotów na skali.
  • Kiedy musisz obliczyć cenę ilości produktów, znając cenę jednostkową.
  • Podobieństwo trójkątów.

Następnie, szczegółowo, istnieją dwie interesujące sytuacje, w których obowiązują proporcjonalne odmiany:

Przykład 1

W skali miasta Hermitage Avenue mierzy 3.2 cm, jest jego prawdziwą długością 400 m. Z drugiej strony ulica La Fuente, która naprawdę mierzy 180 m długości, musi rysować z proporcjonalnie krótszym uderzeniem. Jaki jest rozmiar udaru?

Oświadczenie zawiera pełne informacje o alei Ermita: Niech prawdziwa długość alei i jej długość w samolocie, ponieważ odmiana ma bezpośrednią proporcjonalność, musi:

L = k ∙ ℓ

Na podstawie danych na alei Hermitage możesz znać wartość stałej proporcjonalności K, ale zanim konieczne jest pozostawienie wszystkich długości w tych samych jednostkach:

3.2 cm = 0.032 m

Więc:

400 m = k ∙ 0.032 m

Dlatego stała proporcjonalności jest:

Może ci służyć: jakie są elementy przypowieści? (Części)

K = 400 /0.032 = 12500

Teraz wiadomo, że:

L = 12500 ∙ ℓ

Ten wynik jest interpretowany w następujący sposób: długość ulic na tej mapie jest 12500 razy mniejsza niż jej prawdziwa długość. Dlatego linia ulicy La Fuente mierzy:

ℓ = 180 m/ 12500 = 0.0144 M = 1.44 cm

Przykład 2

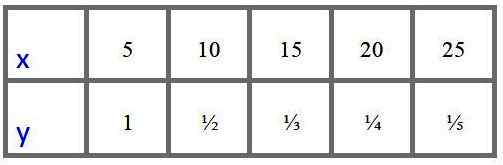
Analityk ma następującą tabelę wartości dla zmiennych „X” i „Y” uzyskanych eksperymentalnie i chce wiedzieć, czy dane te pasują do modelu bezpośredniej zmienności proporcjonalnej, czy jedna z odwrotnej zmienności proporcjonalnej.

Co powinieneś wiedzieć?

Po pierwsze, obserwuje się, że gdy „x” wzrasta, „y” maleje, więc podejrzewa odwrotną proporcjonalność, w każdym razie, aby zapewnić, że analityk ma możliwość oceny, czy iloraz i/x są stałe (proporcjonalne (proporcjonalne Wariacja bezpośrednio) lub jeśli produkt x.i jest stałe (odwrotna zmienność proporcjonalna).

Testowanie z pierwszą opcją:

1 ÷ 5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022 ..

Stwierdzono, że nie jest to bezpośrednia zmienność proporcjonalna, ponieważ iloraz i/x daje różne wartości dla każdej strony danych.

Musimy sprawdzić, czy produkt x ∙ jest stały:

5 × 1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

A jako produkt x ∙ y = 5 stwierdza się, że zmienność ma odwrotną proporcjonalność.

Ta informacja służy do poznania wartości, których nie ma w tabeli, jaka byłaby wartość „y”, gdy x = 30?

Od x ∙ y = 5, „y” jest wyczyszczone i zastąpione x = 30:

y = 5/x

y = 5/30 = 1/6

Ćwiczenie rozwiązane

Jeśli licznik tkaniny kosztuje 6.75 USD i wiedząc, że cena jest bezpośrednio proporcjonalna do kwoty liczników do zakupu, znajdź:

Może ci służyć: antykiwatywne: formuły i równania, przykłady, ćwiczenia

a) Wyrażenie algebraiczne, które łączy zmienne „cena z $” i „Liczba metrów tkaniny”.

b) Przygotuj tabelę wartości z cenami za 3, 6, 9, 12, 15 i 18 metrów tkaniny.

c) wykres uzyskanych wartości.

Odpowiedz

Niech „y” zmienna ”przy $” i „x” zmiennej ilości metrów tkaniny ”. Podobnie jak wprost proporcjonalne, musisz:

y = k ∙ x

Dla x = 1 metr, y = 6.75 USD, a zatem k = 6.75 $/metr. Jest to cena jednostkowa tkaniny, cena dowolnej innej tkaniny „x” jest uzyskiwana przez pomnożenie przez tę wartość, a następnie poszukiwane wyrażenie algebraiczne to:

y = 6.75 ∙ x

Odpowiedź b

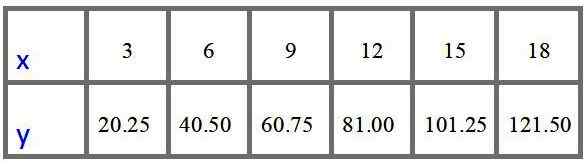
Tabela wartości z cenami za 3, 6, 9, 12, 15 i 18 metrów to:

Odpowiedź c

Wreszcie wykres wartości w poprzedniej tabeli potwierdza, że ​​jest to bezpośrednia zmienność proporcjonalna:

Koszt $ i kwota metrów tkaniny są bezpośrednio proporcjonalne. Źródło: f. Zapata.

Zauważ, że wartość (0,0) jest uwzględniona, ponieważ linia y = 6.75 ∙ x przechodzi przez pochodzenie układu współrzędnych, jak wyjaśniono wcześniej. Ma to sens, ponieważ brak zakupu jest równoważne zakupowi 0 m tkaniny, której wartość wynosi 0 $.

Bibliografia

  1. Larson, r. 2012. Wstępne sculpture. 8. Wydanie. Cengage Learning.
  2. Sekretariat edukacji publicznej Meksyku. Zmienność proporcjonalna. Źródło: PPS.K12.Lub.nas.
  3. Stewart, J. 2007. Kalkulacja wstępna: matematyka do obliczeń. 5. Wydanie. Cengage Learning.
  4. Unam. Przewodniki studiów: matematyka i. Odzyskane z: dirre.Unam.MX.
  5. Zill, d. 2008. Wstępne obliczenie z postępami obliczeniowymi. 4. Wydanie. McGraw Hill.