Trzecie prawo formuł termodynamicznych, równania, przykłady

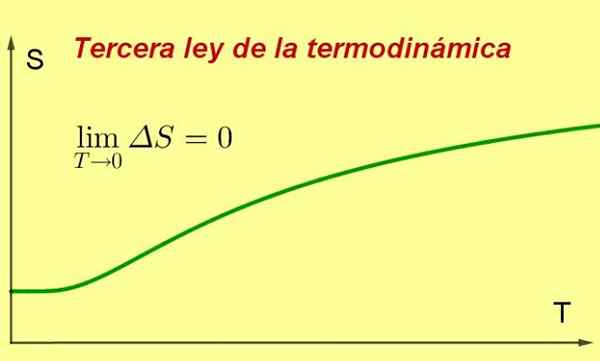
Trzecie prawo termodynamiki stwierdza, że ​​entropia zamkniętego układu termodynamicznego w równowadze jest zwykle minimalna i stała, ponieważ jego temperatura zbliża się do 0 Kelvin.

Ta wartość entropii będzie niezależna od zmiennych systemowych (ciśnienie lub przyłożone pole magnetyczne, między innymi). To, co się dzieje, ponieważ temperatura jest bliższa 0 K, procesy w systemie są zatrzymane i jak entropia jest miarą pobudzenia wewnętrznego, koniecznie schodzi.

Rysunek 1. Gdy temperatura systemu zbliża się do bezwzględnego zeru, jego entropia osiąga minimalną i stałą wartość. Źródło: Przygotowane przez F. Zapata ..

[TOC]

Poprzednie koncepcje

Aby zrozumieć zakres trzeciego prawa termodynamiki, związany z bardzo niskimi temperaturami, konieczne jest przegląd następujących pojęć:

System termodynamiczny

Zwykle odnosi się do gazu, cieczy lub substancji stałej. To, co nie jest częścią systemu, nazywa się wokół. Najczęstszym układem termodynamicznym jest gaz idealny, który składa się z n cząstek (atomów), które oddziałują tylko poprzez kolizje elastyczne.

Izolowane, zamknięte lub otwarte systemy

Izolowane systemy nie są dozwolone żadnej wymiany ze środowiskiem. Systemy zamknięte nie wymieniają materii ze środowiskiem, ale ciepło. Wreszcie, otwarte systemy mogą wymieniać zarówno materię, jak i ciepło w środowisku.

Makro -altan i mikrostan

Makro -strumień systemu jest zbiorem wartości, które mają jego zmienne: ciśnienie, temperatura, objętość, liczba moli, entropia i energia wewnętrzna. Z drugiej strony mikro -estema -w przypadku idealnego gazu -jest podana przez pozycję i pęd każdej z n cząstek, które to wymyślają, w pewnym momencie. 

Wiele mikrostanów może skutkować tym samym stacją makro. W gazie w temperaturze pokojowej liczba możliwych mikrostanów jest ogromna, ponieważ liczba cząstek, które go wymyślą, różne pozycje i różne energie, które mogą przyjąć. 

Wzory i równania

Entropia, jak powiedzieliśmy, jest termodynamiczną zmienną makroskopową, która mierzy układ zaburzeń molekularnych systemu. Stopień zaburzenia systemu jest większy w zakresie, w jakim liczba możliwych mikrostan jest większa. 

Ta koncepcja jest potrzebna do sformułowania trzeciego prawa termodynamiki w formie matematycznej. Czy to entropia systemu:

Oznacza to, że entropia w zamkniętym systemie nie zmienia.

Entropia jest zmienną stanu makroskopowego, która jest bezpośrednio związana z liczbą możliwego mikrostatu systemu, za pomocą następującego wzoru:

S = k ln (w)

W poprzednim równaniu: S reprezentuje entropię, W liczba możliwych mikrostanów systemu i k To stała Boltzmanna (K = 1.38 x 10^-23 J/k). To znaczy entropia systemu jest k razy naturalny logarytm liczby możliwych mikrostatów.

Obliczanie bezwzględnej entropii substancji

Możliwe jest zdefiniowanie absolutnej entropii czystej substancji na podstawie definicji zmienności entropii:

Gdzie Δq jest nieskończenie małą zmiennością ciepła, a T jest temperaturą. To równanie jest prawidłowe, jeśli proces jest odwracalny (Rev).Jeśli jest to proces izobaryczny - stały ciśnienie, ciepło wymieniane podczas nieskończenie małej zmiany temperatury można zapisać w ten sposób:

δq = n . C_P .Dt

Tutaj CP jest specyficzne ciepło molowe i N liczba moli. Zależność cieplna z molowego ciepła z temperaturą jest faktem uzyskanym eksperymentalnie i znana z wielu czystych substancji.

Może ci służyć: Układ słoneczny: planety, cechy, pochodzenie, ewolucja

Według trzeciego prawa w czystej substancji: 

Więc Absolutna entropia molowej czystej substancji, takiej jak:

W poprzedniej notacji pasek wskazuje, że jest to entropia mol substancji, a superson º oznacza czystą substancję.

Aplikacje

W życiu codziennym trzecie prawo termodynamiki ma niewiele zastosowań, w przeciwieństwie do pierwszego i drugiego prawa. Jest tak, ponieważ jest to zasada, która odnosi się do tego, co dzieje się w systemie, gdy zbliża się do absolutnego 0, ranga rzadkich temperatur.

W rzeczywistości osiągnięcie bezwzględnego lub -273,15 ° C jest niemożliwe (patrz przykład 1 później) Jednak trzecie prawo stosuje się podczas badania odpowiedzi materiałów w bardzo niskich temperaturach. 

Dzięki temu pojawiły się ważne postępy w skróconej materii, na przykład:

-Superflualność (patrz przykład 2 później)

-Nadprzewodnictwo 

-Techniki chłodzenia laserowego 

-Kondensat Bose-Einstein 

-Zbadane gazy Fermi.

Rysunek 2. Zbędny hel płynny. Źródło: Wikimedia Commons.

W wyjątkowo niskich temperaturach zejście entropii pozwala na pojawienie się interesujących zjawisk kwantowych. Dlatego zobaczmy, co stanie się z entropią systemu bardzo niskiej temperatury.

Entropia systemu niskiej temperatury

Kiedy masz idealną krystaliczną substancję, jej minimalna entropia wynosi dokładnie zero, ponieważ jest bardzo schludny. W temperaturach w pobliżu bezwzględnego 0 materia jest w stanie skondensowana (ciecz lub ciało stałe), a wibracje szklane są minimalne.

Niektórzy autorzy uważają alternatywne stwierdzenie trzeciego prawa termodynamiki:

„Jeśli materia kondensuje tworzenie idealnego kryształu, gdy temperatura ma tendencję do absolutnej zeru, entropia ma tendencję do zera”. 

Punktualizujmy niektóre aspekty poprzedniego stwierdzenia: 

- Idealny kryształ to taki, w którym każda cząsteczka jest identyczna, w której struktura molekularna jest powtarzana identycznie w całości.

- Ponieważ temperatura ma tendencję do bezwzględnego zera, wibracje atomowe prawie całkowicie zmniejsza się.

Następnie szkło tworzy jedną możliwą konfigurację lub mikroprzepusta, to znaczy W = 1, I dlatego entropia jest równa zero:

 S = k ln (1) = 0

Ale nie tak długo, jak materiał ochłodzony w pobliżu absolutnego zera tworzy kryształ, a tym bardziej ten kryształ jest doskonały. Dzieje się tak tylko wtedy, gdy proces chłodzenia jest bardzo powolny i odwracalny.

W przeciwnym razie czynniki takie jak zanieczyszczenia obecne w szkle umożliwiłyby istnienie innych mikrostanów. Dlatego W> 1 i entropia byłyby większe niż 0.

Resztkowa entropia

Jeśli proces chłodzenia jest nagły, w tym samym systemie przechodzi przez kolejność stanów nierównowagi, co prowadzi do pokazania materiału. W tym przypadku nie ma struktury krystalicznej i uporządkowanej, ale amorficzna substancja stała, której struktura jest podobna do struktury cieczy. 

W takim przypadku minimalna wartość entropii w pobliżu zero bezwzględnego nie wynosi zero, ponieważ liczba mikrostanów jest znacznie większa niż 1. Różnica między tym entropią a zerową entropią idealnego stanu krystalicznego jest znana jako Resztkowa entropia.

Wyjaśnienie jest takie, że poniżej pewnej temperatury progowej system nie ma innej możliwości niż Occupy.

Może ci służyć: pierwsze prawo termodynamiki: wzory, równania, przykłady

Będą odpowiedzialni za utrzymanie stałej entropii, nawet jeśli temperatura będzie nadal zejść w kierunku bezwzględnego zera.

Przykłady

Przykład 1: Bezwzględne zero i nieokreślanie Heisenberga

Zasada nieokreśloności Heisenberga określa, że ​​niepewność w pozycji i pędu cząstki, na przykład w atomach sieci krystalicznej, nie jest niezależna od drugiej, ale podąża za następującą nierównością:

Δx ⋅ δp ≥ h

Gdzie H jest stałą Plancka. Oznacza to, że niepewność w pozycji pomnożonej przez niepewność w pędu (masa na prędkość) jest większa lub równa stałej Plancka, której wartość jest bardzo mała, ale nie zerowa: H = 6.63 x 10-3. 4 J · s.

A co ma wspólnego z trzecią prawem termodynamiki? Jeśli położenie atomów sieci krystalicznej jest ustalona i precyzyjna (Δx = 0) Wówczas prędkość tych atomów może przybierać dowolną wartość od 0 do nieskończoności. Jest to sprzeczne z faktem, że w absolutnym zero każde ruch agitacji termicznej ustaje.

Wzajemnie, jeśli zaczniemy to przy bezwzględnej zerowej temperaturze, wszystkie pobudzenie przestaje, a pęd każdego atomu sieci wynosi dokładnie zero (Δp = 0), wówczas zasada niepewności Heisenberga sugerowałaby, że nieokreśloność w pozycjach każdego atomu byłaby nieskończona, to znaczy mogą być w dowolnej pozycji. 

W wyniku poprzedniego stwierdzenia liczba mikrostanów miałaby tendencję do nieskończoności, a entropia przybrałaby również nieokreśloną wartość. 

Przykład 2: Superflualność i dziwny przypadek helu-4

W zbędności, która występuje w bardzo niskich temperaturach, materia traci tarcie wewnętrzne między swoimi cząsteczkami, zwane breja. W tym przypadku płyn może krążyć bez tarcia na zawsze, ale problem dotyczy tych temperatur prawie nic nie jest płynne oprócz helu.

Hel i hel 4 (jego najliczniejszy izotop) stanowią wyjątkowy przypadek, ponieważ przy ciśnieniu atmosferycznym i w temperaturach zbliżonych do bezwzględnego zera, hel pozostaje ciekłego. 

Gdy hel-4 jest przesłany w temperaturze poniżej 2.2 K pod ciśnieniem atmosferycznym staje się zbędny. Odkrycie to miało miejsce w 1911 r. W Leyden przez holenderskiego fizyka Heike Kamerlingh Onnes (1853–1926).

Rysunek 3. Holenderski fizyk Heike Kamerlingh Onnes (1853–1926). Źródło: Wikimedia Commons.

Atom Helio-4 to Bosón. Bozony, w przeciwieństwie do fermionów, to cząstki, które mogą zajmować ten sam stan kwantowy. Dlatego bozony nie spełniają zasady wykluczenia Pauli.

Następnie wszystkie atomy helu-4 w temperaturach poniżej 2.2 K zajmuje ten sam stan kwantowy, a zatem nie ma nic więcej niż pojedynczy możliwy mikrostan, co oznacza, że ​​zbędny hel-4 ma s = 0.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Rozważ prosty przypadek składający się z układu utworzonego tylko przez trzy cząstki, które mają trzy poziomy energii. Dla tego prostego systemu:

a) Określ liczbę możliwych mikrostanów dla trzech zakresów temperatury:

-wysoki 

-Połowa 

-Niski

b) Określ przez entropię równania Boltzmanna w różnych zakresach temperatury. 

c) Omów wyniki i wyjaśnij, czy zaprzeczać trzeciemu prawu termodynamiki.

Rozwiązanie

W skali molekularnej i atomowej energie, które system może przyjąć. Ponadto, gdy temperatury są tak niskie, cząstki, które tworzą system, mają tylko możliwość zajęcia mniejszych poziomów energii. 

Może ci służyć: indukcja magnetyczna: wzory, jak jest obliczane i przykłady

Wysoka temperatura

Jeśli system ma stosunkowo wysoką temperaturę, cząstki mają wystarczającą ilość energii, aby zajmować dowolny dostępny poziom, co daje 10 możliwych mikrostan, które pojawiają się na poniższym rysunku:

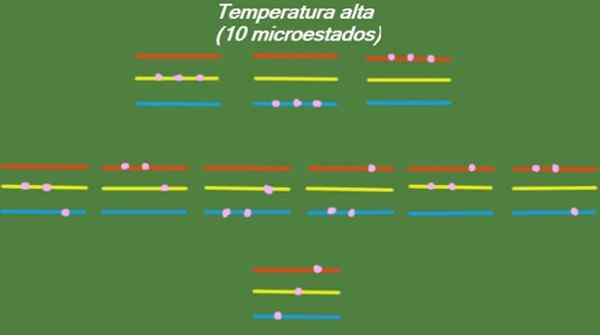Rysunek 4. Możliwe stany w wysokiej temperaturze w roku rozwiązane 1. Źródło: Przygotowane przez F. Zapata.

Średnia temperatura

W przypadku, gdy system ma średnią temperaturę, wówczas cząstki, które go czynią, nie mają wystarczającej ilości energii, aby zajmować najwyższy poziom energii. Możliwe mikrostany są zilustrowane na rysunku:

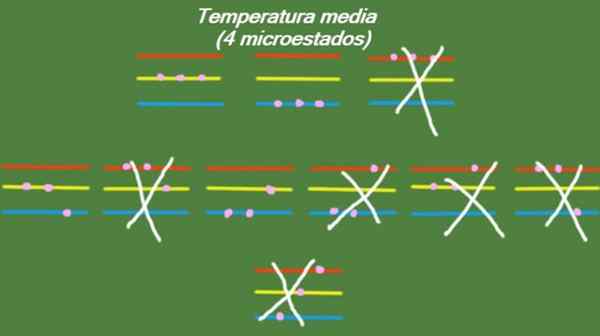Rysunek 5. Micro -State w średniej temperaturze dla rozwiązanego układu ćwiczeń 1. Źródło: Przygotowane przez F. Zapata.

Niska temperatura

Jeśli temperatura nadal opada w naszych wyidealizowanych trzech cząstkach i trzech poziomach energii, cząstki będą miały tak mało energii, że mogą zajmować tylko najniższy poziom. W takim przypadku istnieje tylko 1 możliwy mikrostan, jak można zobaczyć na rycinie 6:

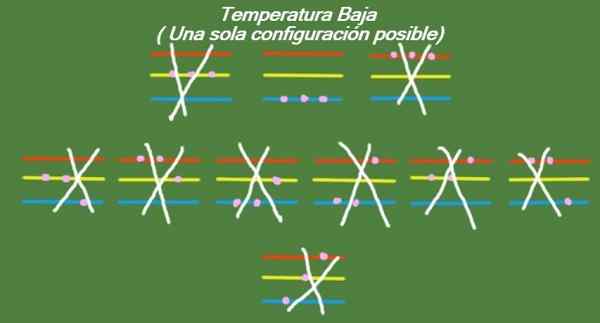Rysunek 6. W niskiej temperaturze istnieje możliwa konfiguracja (własne opracowanie)

Rozwiązanie b

Znany już liczba mikrostanów w każdym zakresie temperatur, możemy już użyć równania Boltzmanna podanego wcześniej, aby znaleźć entropię w każdym przypadku.

S = k ln (10) = 2.30 x k = 3.18 x 10-23 J/k (Wysoka temperatura)

S = k ln (4) = 1.38 x k = 1.92 x 10-23 J/k (Średnia temperatura)

I w końcu:

S = k ln (1) = 0 (Niska temperatura)

Rozwiązanie c

Po pierwsze, zauważamy, że entropia maleje w miarę spadku temperatury, zgodnie z oczekiwaniami. Ale w przypadku najniższych wartości temperatury osiągana jest wartość progowa, z której osiągany jest status podstawowy systemu.

Nawet jeśli temperatura jest tak bliska, jak to możliwe do bezwzględnego zera, nie ma dostępnych stanów mniejszych. Następnie entropia utrzymuje stałą minimalną wartość, która w naszym przykładzie to s = 0.

Ćwiczenie to ilustruje, na poziomie mikrostanów systemu, powód, dla którego trzecie prawo termodynamiki jest spełnione.

- Ćwiczenie 2

Powód, jeśli następne stwierdzenie jest prawdziwe lub fałszywe:

„Entropia systemu w bezwzględnej temperaturze zero wynosi dokładnie zero”.

Uzasadnić odpowiedź i opisz niektóre przykłady.

Rozwiązanie

Odpowiedź brzmi: fałsz.

Przede wszystkim nie można osiągnąć temperatury bezwzględnej, ponieważ zasada niepewności Heisenberga i trzecie prawo termodynamiki zostaną naruszone. 

Bardzo ważne jest, aby zauważyć, że w trzecim prawie nie jest powiedziane to, co dzieje się w bezwzględnym 0, ale gdy temperatura jest nieskończenie blisko absolutnego 0. Różnica jest subtelna, ale znacząca.

Trzecie prawo nie potwierdza, że ​​gdy temperatura przybiera wartość arbitralnie zbliżoną do bezwzględnego zera, entropia ma tendencję do zera. Stało się to tylko w wcześniej analizowanym przypadku: idealny kryształ, który jest idealizacją.

Wiele mikroskopowych systemów skali, czyli w skali kwantowej, ma poziom podstawy energii zdegenerowany, Co oznacza istnienie kilku konfiguracji na najniższym poziomie energii. 

Powyższe oznacza, że ​​w tych systemach entropia nigdy nie byłaby dokładnie zerowa. Entropia nie byłaby dokładnie zerowa w systemach, które są obludzone, gdy temperatura ma tendencję do absolutnej zerowej. W tym przypadku Resztkowa entropia Przed widzianym.

Dzieje się tak, ponieważ ich cząsteczki „utknęły”, zanim zajęją najniższe dostępne poziomy energii, co znacznie zwiększa liczbę możliwych mikrostanów, co uniemożliwia, aby entropia wynosiła dokładnie zero.

Bibliografia

1. Cengel i. 2012. Termodynamika. 7. edycja. McGraw Hill. 347.
2. Jet Propulsion Laboratory. Najfajniejsze miejsce we wszechświecie. Odzyskany z: coldatomlab.Jpl.garnek.Gov.
3. González, a. Entropia i spontaniczność. Odzyskane z: Geocities.WS
4. Quora. Co to jest praktyczne zastosowanie trzeciego prawa termodynamiki?. Odzyskane z: Quora.com
5. Chemia ogólna. Trzecia zasada termodynamiki. Odzyskany z: Korynta.PUCP.Edu.pe
6. Trzecie prawo termodynamiki. Odzyskane z: YouTube.com
7. Wikipedia. Entropia resztkowa. Źródło: w:.Wikipedia.com
8. Wikipedia. Trzecie prawo termodynamiki. Źródło: w:.Wikipedia.com