Toricelli Twierdzenie

Co to jest twierdzenie Torricelli?

On Toricelli Twierdzenie o Torricelli Zasada stwierdza, że ​​prędkość cieczy wychodzącej przez otwór w ścianie zbiornika lub pojemnika jest identyczna, z którą obiekt nabywa swobodnie z wysokości równej wolnej powierzchni cieczy do Dziura.

Twierdzenie jest zilustrowane na poniższym rysunku:

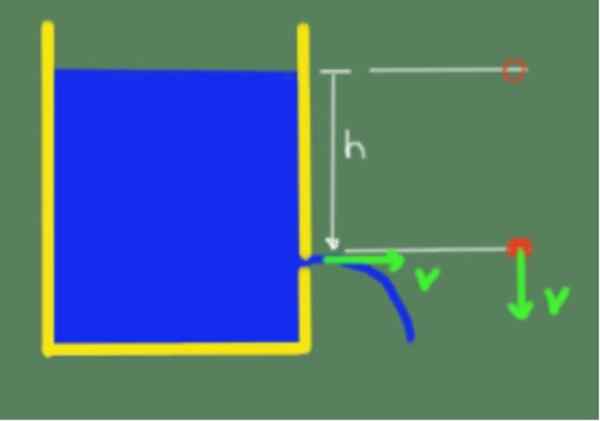Ilustracja twierdzenia Torricelli. Źródło: Self Made.

Z powodu twierdzenia Torricelli możemy następnie powiedzieć, że prędkość wyjściowej cieczy przez otwór, który jest do wysokości H poniżej wolnej powierzchni cieczy, jest podany przez następujący wzór:

Gdzie g jest przyspieszeniem grawitacji, a H jest wysokością od otworu do wolnej powierzchni cieczy.

Ewangelista Torricelli był sylwetką i matematykiem urodzonym w mieście Faenza we Włoszech w 1608 roku. Torricelli przypisuje się wynalezieniu barometru rtęci, aw rozpoznawaniu istnieje jednostka ciśnieniowa zwana „Torr”, równoważna rtęciom milimetrowym (mm Hg).

Demonstracja twierdzenia

W twierdzeniu Torricelli i w formule, która daje prędkość, zakłada, że ​​straty z powodu lepkości są nikczemne, ponieważ w wolnym upadku zakłada się, że tarcie z powodu powietrza otaczającego spadającego obiektu jest nieznaczne.

Poprzednie założenie jest w większości przypadków uzasadnione, a także implikuje zachowanie energii mechanicznej.

Aby zademonstrować twierdzenie, przede wszystkim znajdziemy wzór prędkości dla obiektu uwalnianego z zerową początkową szybkością, z tej samej wysokości co powierzchnia cieczy w zbiorniku.

Może ci służyć: trzy -wymiarowe fale: koncepcja, typy i przykłady

Zasada ochrony energii zostanie zastosowana w celu uzyskania prędkości obiektu, który spadnie tylko wtedy, gdy spadnie wysokość H równe od otworu do wolnej powierzchni.

Ponieważ nie ma strat tarcia, ważne jest zastosowanie zasady oszczędzania energii mechanicznej. Załóżmy, że obiekt, który upada ma masę m, a wysokość H jest mierzona na poziomie wyjściowej płynu.

Obiekt, który spada

Gdy obiekt jest uwalniany z wysokości równej swobodnej powierzchni cieczy, jego energia jest tylko potencjałem grawitacyjnym, ponieważ jego prędkość wynosi zero, a zatem jego energia kinetyczna wynosi zero. EP potencjalnej energii jest podany przez:

EP = M G H

Kiedy idzie przed otworem, jego wysokość wynosi zero, wówczas energia potencjalna wynosi zero, więc ma tylko energię kinetyczną EC podaną przez:

EC = ½ m V²

Ponieważ energia jest zachowana EP = EC tego, co uzyskuje się:

½ m v² = m g h

Oczyszczanie prędkości v Następnie uzyskuje się wzór Torricelli:

Płyn, który wychodzi z dziury

Następnie znajdziemy prędkość wyjścia cieczy przez otwór, aby wykazać, że pokrywa się ona z tym, który został po prostu obliczony dla obiektu, który spada swobodnie.

W tym celu będziemy polegać na zasadzie Bernoulliego, która jest niczym więcej niż ochroną energii stosowanej do płynów.

Zasada Bernoulliego jest sformułowana w ten sposób:

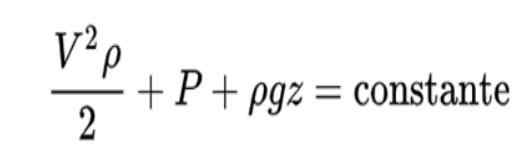
Interpretacja tej formuły jest następująca:

• Pierwszy termin reprezentuje energię kinetyczną płynu na jednostkę objętości
• Drugi reprezentuje prace wykonane przez ciśnienie na jednostkę powierzchni poprzecznej
• Trzeci reprezentuje grawitacyjną energię potencjalną na jednostkę objętości płynu.

Może ci służyć: szybkość natychmiastowa: definicja, wzór, obliczenia i ćwiczenia

Gdy zaczynamy od założenia, który jest idealnym płynem, w warunkach niezamorowych o stosunkowo niskich prędkościach, należy potwierdzić, że energia mechaniczna na jednostkę objętości w płynie jest stała we wszystkich regionach lub odcinkach poprzecznych tego samego.

W tej formuła V to prędkość płynu, ρ Gęstość płynu, P presja i z Pozycja pionowa.

Na rysunku, który pojawia się poniżej, formuła Torricelli jest wykazana na podstawie zasady Bernoulliego.

Stosujemy formułę Bernoulli na wolnej powierzchni cieczy, którą oznaczamy dla (1) i w otworze wyjściowym, który oznaczamy przez (2). Poziom wysokości zerowej został wybrany z otworem wyjściowym.

Zgodnie z założeniem, że przekrój w (1) jest znacznie większy niż w (2), możemy następnie założyć, że prędkość spadku cieczy w (1) jest praktycznie zaniedbana.

Dlatego V został umieszczony₁= 0, ciśnienie, do którego ciecz jest poddawany (1), to ciśnienie atmosferyczne, a wysokość mierzona z otworu wynosi H.

Dla sekcji wyjściowej (2) Zakładamy, że prędkość wyjściowa wynosi v, ciśnienie, do którego podlega ciecz do wylotu, to ciśnienie atmosferyczne, a wysokość wyjściowa wynosi zero.

Wartości odpowiadające sekcjom (1) i (2) są zastąpione w wzorze Bernoulli i równe. Równość jest ważna, ponieważ zakładamy, że płyn jest idealny i nie ma lepkich strat tarcia. Po uproszczeniu wszystkich warunków prędkość jest uzyskiwana w otworze wyjściowym.

Może ci służyć: czerwony krasnolud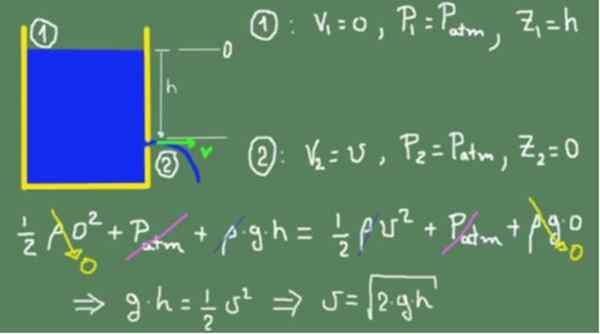

Poprzednie pole pokazuje, że uzyskany wynik jest taki sam, jak obiekt, który spada swobodnie,

Z tym, co jest wykazane zasadą Torricelli.

Rozwiązane ćwiczenia

Ćwiczenie 1

Siema) Mała rura wylotowa zbiornika wodnego znajduje się 3 m pod powierzchnią wody. Oblicz prędkość wylotu wody.

Rozwiązanie:

Poniższy rysunek pokazuje, w jaki sposób formuła Torricelli jest stosowana do tego przypadku.

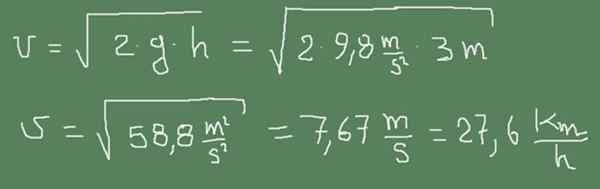
Ćwiczenie 2

Ii) Zakładając, że rurka wyjściowa poprzedniego zbiornika wysiłku ma średnicę 1 cm, oblicz przepływ wylotu wody.

Rozwiązanie:

Przepływ jest objętością cieczy, która wychodzi na jednostkę czasu i jest po prostu obliczany przez pomnożenie powierzchni otworu wyjściowego przez prędkość wyjściową.

Poniższy rysunek pokazuje szczegóły obliczeń.

Ćwiczenie 3

Iii) Określ, jak wysokość jest wolna powierzchnia wody w pojemniku, jeśli jest znana

że w otworze u dołu pojemnika woda wynosi 10 m/s.

Rozwiązanie:

Nawet gdy otwór znajduje się na dole pojemnika, można zastosować formułę Torricelli.

Poniższy rysunek pokazuje szczegóły obliczeń.

Bibliografia

1. Wikipedia. Toricelli Twierdzenie.
2. Hewitt, str. Konceptualna nauka fizyczna. PIĄTA EDYCJA.119.
3. Młody, Hugh. 2016. Sears-Zansky's University Physics z nowoczesną fizyką. 14. edycja. osoba. 384.