Kwadratowe przykłady, reguły i ćwiczenia rozwiązane

Kwadratowe sukcesy, W kategoriach matematycznych składają się one z sekwencji liczb, które są zgodne z pewną regułą arytmetyczną. Ciekawe jest znanie tej zasady ustalenie któregokolwiek z warunków sukcesji.

Jednym ze sposobów osiągnięcia tego jest określenie różnicy między dwoma kolejnymi terminami i sprawdzenie, czy uzyskana wartość jest zawsze powtarzana. Kiedy tak mówi się, że jest to regularna sukcesja.

Sukcesje numeryczne to sposób na organizację sekwencji liczbowych. Źródło: Pixabay.com

Ale jeśli nie jest powtarzane, możesz spróbować zbadać Różnica między różnicami I sprawdź, czy ta wartość jest stała. Jeśli tak, to jest to Kwadratowa sukcesja. 

[TOC]

Przykłady regularnych sukcesji i kwadratowych sukcesji

Poniższe przykłady pomagają wyjaśnić, co zostało wyjaśnione do tej pory:

Przykład regularnej sukcesji

Być sukcesją S = 4, 7, 10, 13, 16, ...

Ta sukcesja, oznaczona przez S, jest nieskończonym zestawem liczbowym, w tym przypadku liczb całkowitych.

Można zauważyć, że jest to regularna sukcesja, ponieważ każdy termin jest uzyskiwany przez dodanie 3 do poprzedniego terminu lub elementu:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Innymi słowy: ta sukcesja jest regularna, ponieważ różnica między następującym terminem a poprzednim daje ustaloną wartość. W przykładzie, biorąc pod uwagę, że ta wartość to 3.

Nazywane są również regularne sukcesje uzyskane przez dodanie stałej kwoty do poprzedniego okresu Postępy arytmetyczne. I różnica - stała - między kolejnymi terminami powód I jest oznaczony jako r.

Przykład sukcesji nieregularnej i kwadratowej

Zobacz teraz następującą sukcesję:

S = 2, 6, 12, 20, 30, .. .

Po obliczaniu kolejnych różnic uzyskuje się następujące wartości:

Może ci służyć: losowe wybory z lub bez zamiennika

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Ich różnice nie są stałe, więc można powiedzieć, że jest to sukcesja nieregularna.

Jeśli jednak weźmiemy pod uwagę zestaw różnic, istnieje kolejna sukcesja, która zostanie oznaczona jako s_Dif:

S_Dif = 4, 6, 8, 10, .. .

Ta nowa sukcesja to regularna sukcesja, ponieważ każdy termin jest uzyskiwany przez dodanie stałej wartości r = 2 do poprzedniej. Dlatego możemy potwierdzić, że S jest Kwadratowa sukcesja.

Ogólna zasada, aby zbudować kwadratową sukcesję

Istnieje ogólna formuła do zbudowania sukcesji kwadratowej:

T_N = A ∙ n² + B ∙ n +c

W tej formule t_N Jest to termin N sukcesji. A, B i C są ustalonymi wartościami, podczas gdy N zmienia się jeden po drugim, czyli 1, 2, 3, 4, ..

Z sukcesji poprzedniego przykładu a = 1, b = 1 i c = 0. Stamtąd następuje, że formuła generująca wszystkie warunki to: t_N = n² + N

To jest do powiedzenia:

T₁ = 1² + 1 = 2

T₂ = 2² + 2 = 6

T₃ = 3² + 3 = 12

T₅ = 5² + 5 = 30

T_N = n² + N

Różnica między dwoma kolejnymi warunkami kwadratowej sukcesji

T_N+1 - T_N = [A ∙ (n+1)² + B ∙ (n + 1) + c] - [a ∙ n² + B ∙ n +c]

Pozostaje opracowanie wyrażenia za pośrednictwem niezwykłego produktu:

T_N+1 - T_N = A ∙ n² + A ∙ 2 ∙ n + a + b ∙ n + b + c - a ∙ n² - B ∙ n - c

Upraszczając go: otrzymujesz:

T_N+1 - T_N = 2 ∙ a ∙ n + a + b

Jest to formuła, która daje sukcesję różnic_Dif które można napisać w ten sposób:

Dif_N = A ∙ (2n+1)+B

Gdzie wyraźnie następujący termin wynosi 2 ∙ Czasami poprzedni. To znaczy powód sukcesji różnic_Dif Es: r = 2 ∙ a.

Rozwiązane ćwiczenia kwadratowych sukcesji

Ćwiczenie 1

Być sukcesją S = 1, 3, 7, 13, 21,…. Określ tak:

i) To jest regularne lub nie

ii) jest kwadratowy lub nie

iii) był kwadratowy, sukcesja różnic i ich powód

Może ci służyć: Limit właściwości (z przykładami)

Odpowiedzi

i) Obliczmy różnicę następującego terminu i poprzedniego:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

Możemy potwierdzić, że sukcesja S nie jest regularna, ponieważ różnica między kolejnymi terminami nie jest stała.

ii) sukcesja różnic jest regularna, ponieważ różnica między jej warunkami jest stałą wartością 2. Dlatego pierwotna sukcesja jest kwadratowa.

iii) już ustaliliśmy, że S jest kwadratowe, sukcesja różnic to:

S_Dif = 2, 4, 6, 8,…, a jego powodem jest r = 2.

Ćwiczenie 2

Być sukcesją S = 1, 3, 7, 13, 21,… z poprzedniego przykładu, w którym zweryfikowano, że jest kwadratowy. Określić:

i) wzór, który określa ogólny termin t_{N .}

ii) Sprawdź trzeci i piąty okres.

iii) wartość dziesiątego okresu.

Odpowiedzi

i) ogólna formuła t_N jest ∙ n² + B ∙ n +c. Wtedy wiadomo, że wartości A, B i C.

Sukcesja różnic jest właściwa 2. Oprócz jakiejkolwiek sukcesji kwadratowej przyczyną R jest 2 ∙ A, jak pokazano w poprzednich sekcjach.

R = 2 ∙ a = 2, co prowadzi nas do stwierdzenia, że ​​a = 1.

Pierwszy termin sukcesji różnic s_Dif Jest to 2 i musi być zgodne z ∙ (2n+1)+B, z n = 1 i a = 1, to znaczy:

2 = 1 ∙ (2 ∙ 1+1)+B

Oczyszczanie B jest uzyskiwane: B = -1

Następnie pierwszy termin s (n = 1) Vale 1, to znaczy: 1 = a ∙ 1² + B ∙ 1 + C. Jak już wiemy, że a = 1 i b = -1, zastępując nas, pozostajemy:

1 = 1 ∙ 1² + (-1) ∙ 1 +c

Oczyszczanie C jest uzyskiwane jego wartość: C = 1.

W podsumowaniu:

A = 1, b = -1 i c = 1

Wtedy termin jest po prostu_N = n² - N + 1

ii) Trzeci termin t₃ = 3² - 3 + 1 = 7 i jest weryfikowany. Piąty t₅ = 5² - 5 + 1 = 21, co jest również weryfikowane.

iii) Dziesiąty termin będzie t₁₀ = 10² - 10 + 1 = 91.

Ćwiczenie 3

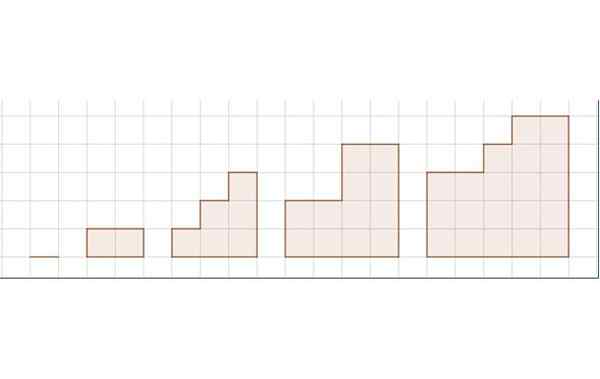Sekwencja obszarów do ćwiczeń 3. Źródło: Self Made.

Rysunek pokazuje sekwencję pięciu figur. Siatnica reprezentuje jednostkę długości.

Może ci służyć: różnica między wspólną frakcją a liczbą dziesiętną

i) określ sukcesję dla obszaru liczb.

i) Pokaż, że jest to sukcesja kwadratowa.

iii) Znajdź obszar rysunku nr 10 (nie pokazano).

Odpowiedzi

i) sukcesja odpowiadająca obszarowi sekwencji figur wynosi:

S = 0, 2, 6, 12, 20,…

ii) sukcesja odpowiadająca kolejnym różnicom warunków S jest:

S_Dif = 2, 4, 6, 8,…

Ponieważ różnice między kolejnymi terminami nie są stałe, więc S nie jest regularną sukcesją. Musi wiedzieć, czy jest kwadratowy, dla którego ponownie tworzymy sekwencję różnic, uzyskując:

2, 2, 2, .. .

Ponieważ wszystkie warunki sekwencji są powtarzane, potwierdza się, że S jest sukcesją kwadratową.

iii) sukcesja s_Dif jest regularny, a jego powodem r to 2. Używając wcześniej wykazanego równania r = 2 ∙ a, pozostaje:

2 = 2 ∙ a, co oznacza, że ​​a = 1.

Drugi termin sukcesji różnic s_Dif To jest 4 i n-em s_Dif Jest

A ∙ (2n+1)+b.

Drugi termin ma n = 2. Ustalono również, że a = 1, więc stosowanie poprzedniego równania i zastąpienie go jest:

4 = 1 ∙ (2 ∙ 2+1)+B

Oczyszczanie B jest uzyskiwane: B = -1.

Wiadomo, że drugi termin S jest wart 2 i że formuła ogólnego terminu musi spełnić n = 2:

T_N = A ∙ n² + B ∙ N +C; n = 2; A = 1; B = -1; T₂ = 2

To jest do powiedzenia

2 = 1 ∙ 2² - 1 ∙ 2 + c

Stwierdzono, że C = 0, to znaczy, że formuła, która daje ogólny termin sukcesji, to:

T_N = 1 ∙ n² - 1 ∙ n +0 = n² - N

Teraz piąty termin jest weryfikowany:

T₅ = 5² - 5 = 20

iii) Rysunek nr 10, który nie został tutaj narysowany, będzie miał obszar odpowiadający dziesiątej okresu sukcesji:

T₁₀ = 10² - 10 = 90

Bibliografia

1. https: // www.Geogebra.org