Reguła korespondencji funkcji

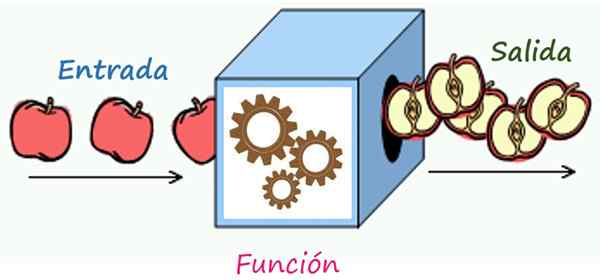
Zasada korespondencji jest mechanizmem przekształcającym elementy wejścia do elementów wyjściowych. Źródło: Wikimedia Commons/F. Zapata

Jaka jest zasada korespondencji funkcji?

Reguła korespondencji funkcji Wskazać sposób, w jaki elementy jednego zestawu są powiązane z elementami innego. Elementy pierwszego zestawu są znane jako domena, i do drugiej, jak Codominium albo Przeciwdziałanie.

Związek lub związek między zestawami można określić instrukcją werbalną lub pisemną, jednak gdy zestawy są numeryczne, reguła korespondencji jest wskazana przez formułę.

Ta formuła zawiera operacje, które należy wykonać za pomocą elementów zespołu początkowego, a tym samym uzyskać serię elementów zawartych w kodominium.

Teraz, gdy związek między elementami jest funkcją, reguła korespondencji spełnia dwa specjalne warunki:

• Do każdego z elementów domeny jest powiązane, poprzez zasadę korespondencyjną, pojedynczy element Codominium, znany jako obraz.
• Innymi słowy, ten obraz jest wyjątkowy, żaden element domeny nie jest powiązany z więcej niż jednym elementem Codominium.

W ten sposób możesz sobie wyobrazić zasadę korespondencji funkcji jako mechanizmu zablokowanego w pudełku. Każda wartość domeny, bez wyjątku, może wprowadzić pole i wydostać się z niego przekształcone, poprzez operacje wskazane przez zasadę korespondencji. Przykłady będą widoczne natychmiast.

Przykłady

Przykład 1

Zasada korespondencji funkcji można wyrazić jako instrukcję pisemną, gdy elementy nie są numeryczne.

Na przykład istnieje zestaw krajów, oznaczony jako P i inny zestaw miast C:

Może ci służyć: U -test of Mann - Whitney: co to jest i po zastosowaniu, wykonanie, przykład

P = Kanada, Meksyk, Hiszpania, USA, Francja, Argentyna, Brazylia, Niemcy

C = Paris, Londyn, Buenos Aires, Berlin, Meksyk, Ottawa, Río, New York, Madryt, Waszyngton, Bern, Rzym, Brasilia, Toronto

Być zasadą korespondencyjną F Między P i C podanym przez:

F: P → C

Gdzie F To jest zasada „… Czyje to kapitał .. ”, Który kojarzy każdy kraj w P (zestaw początkowy), z jego stolicą w C (zestaw przyjazdów).

Na przykład: „Hiszpania, Czyja jest kapitał Madryt". Element „Hiszpania” należy do początkowego zestawu P, a element „Madryt” do całego C, przybycie.

Reprezentację tej funkcji można wykonać za pomocą diagramu Venna lub po prostu za pomocą uporządkowanych par.

Uporządkowane pary zawierają, jak sama nazwa wskazuje, dwa elementy o określonej kolejności, w tym przykładzie pierwszym elementem pary jest kraj, a drugi, jego stolica.

Ze swojej strony schemat Venna jest sposobem na wizualizację funkcji, pokazując zestawy początkowe i przybycia, a także zasadę korespondencji między nimi.

Reprezentacja F jako uporządkowanych par

F = (Kanada, Ottawa); (Meksyk, Meksyk); (Hiszpania Madryt); (USA; Waszyngton); (Paryż, Francja); (Argentyna Buenos Aires); (Brazylia Brasilia); (Niemcy, Berlin)

Pierwsza para kojarzy Kanada, Czyja jest kapitał Ottawa, drugi współpracownik Meksyku, Czyja jest kapitał Meksyk i tak dalej.

Reprezentacja F jako diagram Venna

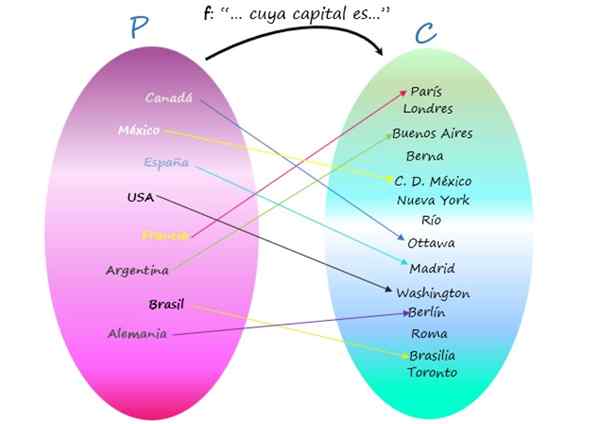
Zauważ, że istnieją miasta, które nie są stolicą żadnego kraju, ponieważ chociaż są to elementy Codominium, nie są one obrazem żadnego elementu zestawu początkowego. Mimo to związek jest funkcją, ponieważ ważne jest to, że każdy kraj ma swój kapitał, a to jest wyjątkowe.

Może ci służyć: obszar regularnego i nieregularnego pięciokąta: jak to jest przyjmowane, ćwiczenia

Podzbiór utworzony przez elementy Codominium, które są obrazem jakiegoś elementu domeny, jest wywoływane Zakres lub funkcja funkcji. Na przykład trasa R of F Jest:

R = Paris, Buenos Aires, Meksyk, Ottawa, Madryt, Berlin, Waszyngton, Brasilia

Warto zapytać, czy można ustalić związek między C i P, gdzie C staje się zestawem początkowym i przybyciem. Odpowiedź brzmi tak, ale nie byłaby to funkcja, ponieważ istnieją miasta, które nie są stolicami, takie jak Nowy Jork, lub kraj, którego są kapitałem, nie pojawiają się wśród elementów kompleksu P, takie jak Rzym.

Przykład 2

Gdy ustawiony odlot i zestaw przyjazdu są numeryczne, zasada korespondencji funkcji, która je łączy. Na przykład bądź opanowaniem funkcji następujący zestaw:

D = 0, 1, 2, 3, 4, 5, 6)

Zasada korespondencji F: D → r, który łączy elementy D z zestawem liczb rzeczywistych r to:

F: „Podwójne”

Jeśli „x” jest elementem zestawu początkowego, f (x) jest odpowiednim elementem zestawu przyjazdu, a reguła korespondencyjna jest napisana w ten sposób:

f (x) = 2x

Codominium to zestaw liczb rzeczywistych. Podzbiór Reais jest drogą tej funkcji, zbiór liczb, którego wartość jest dwa razy jak x:

R = 0, 2, 4, 6, 8, 10, 12

W postaci uporządkowanych par reguła korespondencji powoduje:

F = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Uporządkowane pary mogą być wykresem na płaszczyźnie kartezjańskiej. Pierwszy element momentu obrotowego umieszcza się na osi poziomej, zwany również osą odciętnych lub osi „X”, podczas gdy drugi przechodzi na osi pionowej, osi uporządkowanej lub po prostu osi „y”:

Może ci służyć: nieruchomość dystrybucyjna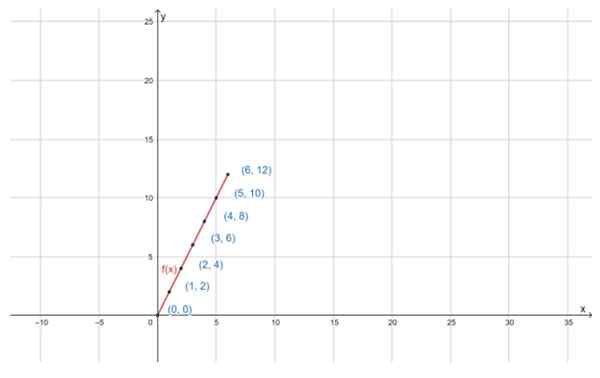 Wykres funkcji f (x) = 2x, dla określonej domeny D, jest linią prostą. Źródło: f. Zapata przez Geogebra

Ćwiczenia

Określ zasadę korespondencji dla następujących relacji, wskazując, czy są to funkcje. Zestaw naturalnych liczb to n, a prawdziwy jest r.

Wskaż także domenę, Codominium i drogę funkcji, w przypadkach, w których odpowiada:

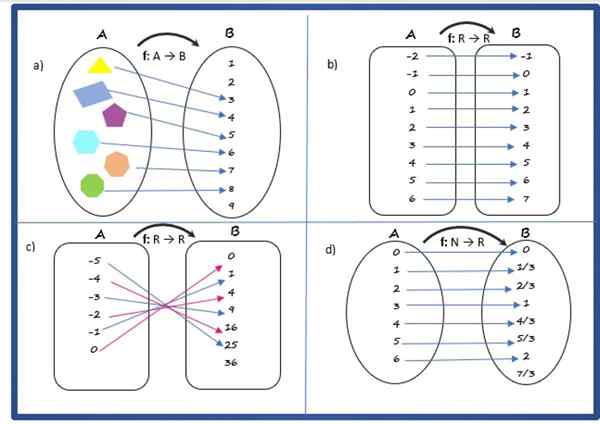
Rozwiązanie

Jest to funkcja, ponieważ każdy element zestawu początkowego, składający się z wielokątów, ma unikalny obraz w zestawie przyjazdu.

Reguła korespondencyjna dotyczy wielokąta z liczbą jego boków, domena składa się z zestawu A wielokątów:

A = trójkąt, czworobok, pentagon, sześciokąt, heptagon, ośmiokąt

Codominium to zestaw pierwszych liczb naturalnych, w tym 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

A CO C są liczbami naturalnymi od 3 do 8:

C = 3, 4, 5, 6, 7, 8

Rozwiązanie b

Jest to funkcja, ponieważ spełnia warunki określone powyżej.

Zasada korespondencji to:

f (x) = x + 1

Reguła korespondencji wskazuje, że funkcja jest zdefiniowana przez r → r, dlatego domena jest zbiorem liczb rzeczywistych. A co -ooominium i trasa również zbiegają się z prawdziwym.

Rozwiązanie c

Jest to funkcja z zasadą korespondencyjną:

f (x) = x²

Domena i kodominium są zestawem reais, ale droga składa się tylko z pozytywnych liczb rzeczywistych, oznaczonych jako r⁺ i w tym 0.

Rozwiązanie d

To jest funkcja. Jego zasada korespondencyjna to:

f (x) = x/3

Jego domena jest zbiorem liczb naturalnych N i Codominium, a także trasą, to rzeczywiste liczby n.